点吸式波浪能装置的功率特性研究
杨雨浓,谢鹏,郑雄波
1.哈尔滨工程大学动力与能源工程学院,黑龙江哈尔滨 150001 2.哈尔滨工程大学理学院,黑龙江哈尔滨 150001
点吸式波浪能装置的功率特性研究
杨雨浓1,谢鹏2,郑雄波2
1.哈尔滨工程大学动力与能源工程学院,黑龙江哈尔滨 150001 2.哈尔滨工程大学理学院,黑龙江哈尔滨 150001
基于线性规则波理论针对固定式点吸收波浪能发电装置进行研究,通过数值计算,分析了锥形浮子与圆柱形浮子在无阻尼和有阻尼条件下在波浪作用下的运动规律,探索浮子的运动响应和装置的能量转换效率与浮子形状、波浪频率或周期以及PTO系统阻尼之间的内在关系,寻求进行固定式点吸收波能装置最优化设计的方法。通过计算和分析,提出了浮子结构和PTO系统阻尼特性对装置能量转换特性的影响规律,该结论可为点吸式波浪能转换装置的理论研究和工程应用提供参考和借鉴。
点吸式;波浪能装置;海洋能;系统阻尼特性;能量转换效率
为了保证人类所需要的能源能够得到稳定并且持久的发展,世界各国均在努力地使能源结构从单一的常规能源向多种新能源过度。海洋波浪能作为一种清洁的可再生能源,具有储量大、分布广、环境污染小等特点,日益受到沿海各国的高度重视[1-2]。
波浪能发电装置按其吸收能量的方式划分主要有振荡水柱式、收缩波道式、摆式、点吸式等[3]。其中振荡水柱式波浪能转换装置是一种典型的岸基式波能发电技术,由于这种装置具有较高的可靠性,在一些附近海域波能密度较高的国家,如许多欧洲国家得到了重点发展。我国附近海域的波能密度与欧洲国家相比要低得多,约为他们的20%~25%,所以在我国采用振荡水柱式波能装置就显得不太理想[4]。点吸式波浪能发电装置是一种利用尺寸远小于波长的浮子捕获波浪能的装置。与其他装置相比,点吸式装置适合小波浪条件,而且结构简单,成本较低[5-6],因此点吸式波装置是目前各国研制的重点装置形式之一。本文从运动学和能量转换的角度,针对固定式点吸收波浪能装置进行研究,建立浮子在波浪中的动力学方程,针对锥形浮子和圆柱形浮子进行水动力数值计算,研究其在波浪中的运动响应,分析浮子的运动机理和点吸式波浪能装置的能量转换特性,为点吸式波浪能装置的研制提供一定的理论基础和参考依据。
1 装置的运动学原理
本文以单点吸收的固定式波浪能装置为研究对象,该装置包括浮子、PTO系统和固定式载体3个基本模块,浮子与PTO系统均安装于载体之上。在波浪作用下,浮子吸收波浪能量以一定的方式运动,本文中对浮子的运动受到连接件的约束,其运动模式为单自由度的垂荡运动,浮子的运动推动PTO系统运动,PTO的阻尼力做功将机械能转化为电能或其他形式的能量。该装置可简化如图1所示。

图1 质量-弹簧-阻尼系统
假设流体是理想的,有势无旋,并假设波高远小于波长。将浮子平均湿表面sH,自由面sF,底部sB和远方控制面sC围成一个空间流体域,记总的速度势为Φ(x,y,z),把时间因素和空间因素分离可得:
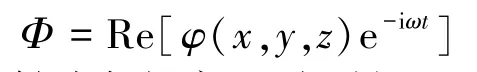
式中:ω为入射波角频率,t为时间,φ(x,y,z)为规范化速度势。
浮子受到的流体动力

式中:ukj为附加质量,λkj为兴波阻尼系数,Xj(j=1,2,…,6)表示浮体的6自由度运动[7]。
本文中由于约束的作用,浮子只做垂直方向的升沉运动。假设由于水对浮子表面的压力产生的垂直方向的力为fh(t),由于功率输出系统对浮子产生的力为fPTO,m为浮子质量,z为浮子在垂直方向的位移。根据牛顿第二定律,浮子的动力学方程为

式中:fez为由入射波产生的波浪激励力,frz为由浮子运动产生的垂直方向上的辐射作用力,fs静水回复力,C为系统的粘性阻尼系数,K装置振动系统的弹性系数,一般来说漂浮式装置的弹性系数即为锚链的刚度,固定式装置的弹性系数为0。
设浮子作垂荡运动的复数运动振幅为X0,则

其频域方程为

式中:A与B分别为浮子的附加质量和阻尼系数。由式(4)可得:

当浮子在波浪上做垂荡运动时,浮子所吸收的波浪能量等于功率输出系统阻尼力所做的功[8],因此浮子从波浪中吸收的功率为
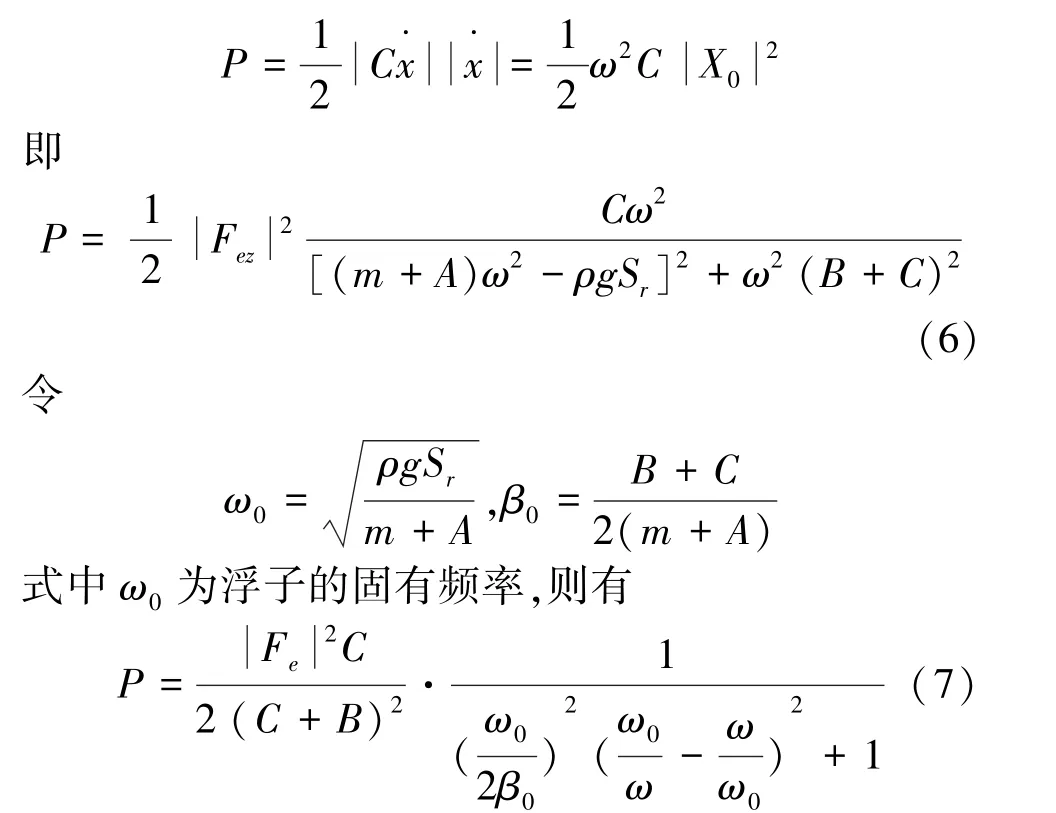

2 浮子水动力计算
浮子浮于水面,波浪作用下,浮子的运动有6个模态,在线性自由面和物面条件下,浮子所在流场的第j模态下时规范化速度势φj(x,y,z,t)(j=1,2,…,6)定解问题的数学方程为

规范化速度势的求解是计算浮子水动力系数的关键环节。规范化速度势采用间接边界元法进行求解,其边界积分方程为
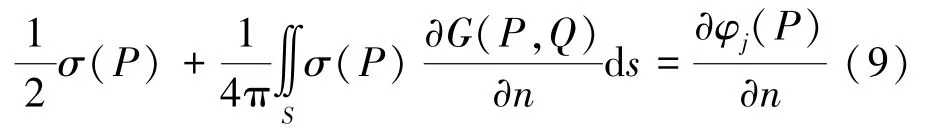
将边界面划分为n个边界单元,各单元内的σ(P)为常量,对式(9)进行离散,解所得代数方程,求出边界元的σ值,流场中任意一点的规范化速度势为[9]
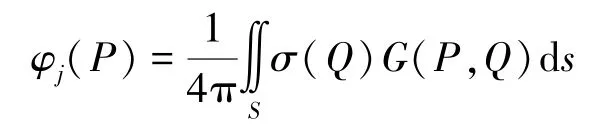
本文针对图2所示的2种浮子进行计算。

图2 浮子形状
静水状态下2种浮子的水线位置相同,其参数如表1所示。

表1 浮子参数
3 运动响应与能量转换特性分析
下面通过频域水动力计算,分析固定式点吸式装置以上述2种浮子作为能量捕获机构时,在波浪与PTO系统共同作用下,浮子的运动响应以及装置的能量转换特性。在以下计算中,海洋环境参数为:水深10 m,波幅1 m,波浪圆频率范围为0.2~6 rad/s,对应的周期为1.1~31.4 s,假设PTO系统的阻尼为线性阻尼,忽略摩擦阻力等造成的能量损耗。
3.1 浮子的运动响应
分别计算2种浮子的水动力,考虑PTO系统具有不同的线性阻尼系数,通过式(5)计算2种浮子在不同阻尼条件下浮子的运动响应幅值。本文考虑PTO系统具有以下3种阻尼系数:0 N·s/m(无阻尼)、1 000 N·s/m(阻尼1)、5 000 N·s/m(阻尼2)。图3所示为2种浮子在3种阻尼条件下的运动响应曲线,横坐标为波浪圆频率,纵坐标为浮子的运动振幅与波高的比值。

图3 浮子的运动响应曲线
针对图3中浮子的运动响应曲线,分别从以下几方面进行分析:
1)无阻尼条件下,浮子的运动响应规律。从图3可以看出,相同波浪频率时,浮子的运动振幅比有阻尼时大,振幅随着波浪频率的增加而缓慢增加,在某一频率点处达到最大值,然后开始加速递减,最大振幅超过波高。通过计算可知,锥形浮子的固有频率为4.27 rad/s,柱形浮子的固有频率为4.07 rad/s,因此,无外部机械阻尼时,锥形浮子会在波浪频率为4.27 rad/s左右时发生共振,而柱形浮子会在波浪频率为4.07 rad/s左右时发生共振,共振点即图中浮子运动振幅的最大值点,此时入射波能量以最高的效率被浮子吸收转化为浮子的机械能,由于PTO系统阻尼为0,浮子没有能量输出。
2)有阻尼条件下,浮子的运动响应规律。在给浮子施加外部机械阻尼之后,浮子的运动振幅明显减小,阻尼越大,运动振幅越小,这是因为在给浮子施加外部机械阻尼之后,浮子吸收的波浪能在转化为浮子机械能的同时,另一部分转化为PTO系统的能量进行输出,从而导致浮子的振幅变小。如果浮子吸收相同的波浪能,浮子的振幅越小,说明PTO系统的能量输出越大,系统的转化效率越高。
3)锥形浮子与圆柱形浮子的运动响应差别。通过比较可知,在相同阻尼条件下,当波浪频率小于4.2 rad/s时,柱形浮子的振幅略大,而4.2 rad/s之后,锥形浮子的振幅略大,当有阻尼时,二者的差别很小,阻尼越大,差别越小。
4)装置的能量转换特性。针对锥形浮子和柱形浮子,以及不同的PTO阻尼条件,分析装置的能量转换特性。当PTO系统阻尼为0时,系统不发生能量转换,这里考虑PTO系统阻尼系数为500 N·s/m(阻尼1)、1 000 N·s/m(阻尼2)、5 000 N·s/m(阻尼3)3种条件下的具体性能。图4所示为浮子的能量转换曲线,图中横坐标为波浪圆频率,纵坐标为PTO系统的输出功率与浮子宽度内入射波功率的比值,浮子宽度内入射波功率为
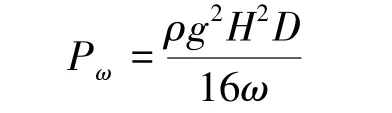
式中:ρ为海水密度,H为波高,ω为波浪圆频率,D为浮子宽度。

图4 装置的能量转换曲线
在波浪和PTO系统的共同作用下,浮子吸收波浪能,并通过阻尼力做功由PTO系统输出能量。下面针对图4中装置的能量转换曲线,从以下几方面进行分析。
1)装置的能量转换效率随入射波频率的变化规律。从图4中装置的能量转换曲线可以看出,随入射波频率的增加,装置的输出功率呈先递增再递减的变化趋势,在某一波浪频率处达到最大值,该波浪频率即为装置的最优转换频率,起变化趋势与海洋波浪的能量谱密度函数曲线的变化趋势相似。相关结果的对应关系如表2所示。
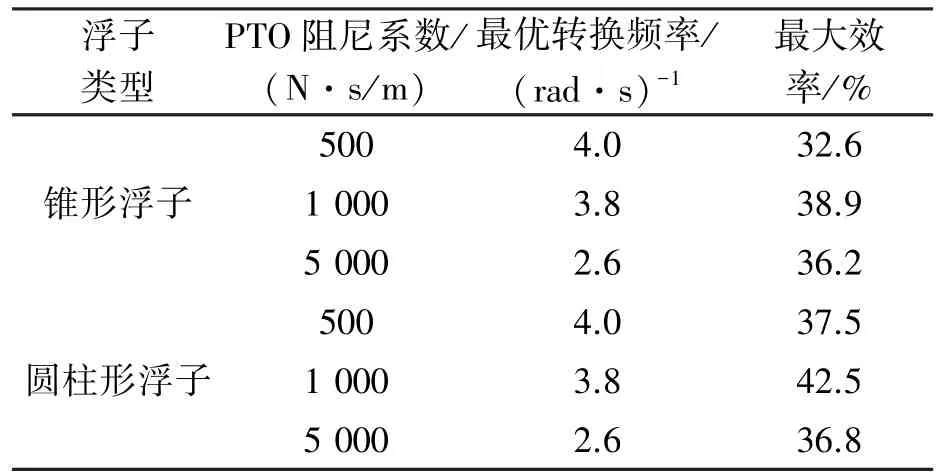
表2 装置的最大转化效率及其对应的相关参数
2)PTO阻尼对装置能量转换效率的影响规律。通过同一浮子的曲线进行比较可以看出,装置能量转换效率随PTO阻尼的变化规律与浮子的运动响应规律不同,PTO系统阻尼系数为1 000 N·s/m时,装置的输出功率最大值大于其他2种情况(500 N·s/m、5 000 N·s/m)的最大值,即当PTO系统的线性阻尼系数从小到大变化时,装置的输出功率的最大值也随之变化,且呈先增加后减小的趋势,同时装置的最大输出功率所对应的波浪频率逐渐减小。当阻尼增加时,浮子的振幅减小,但PTO系统的能量转化效率并没有单调增加,这说明PTO系统的阻尼不仅影响从浮子到PTO系统的能量输出,同时也会影响浮子从波浪吸收能量的效率,不同波浪条件下,存在最优阻尼系数,PTO系统的阻尼是影响装置能量转换效率的重要因素之一,在实海况条件下,当装置的最大输出功率所对应的波浪频率等于海域波浪能的峰值频率时,装置具有最优的转换效率,而此时PTO系统组尼为该海况下装置的最优阻尼。
3)通过对采用锥形浮子装置和圆柱形浮子装置的能量转曲线进行比较可以看出,当PTO系统的阻尼系数为500 N·s/m时,若波浪圆频率小于4.2 rad/s,圆柱形浮子装置的效率高于锥形浮子装置,若波浪圆频率大于4.2 rad/s,则结果相反;当PTO系统的阻尼系数为1 000 N·s/m时,若波浪圆频率小于4.2 rad/s,圆柱形浮子装置的效率高于锥形浮子装置,若波浪圆频率大于4.2 rad/s,则结果相反;当PTO系统的阻尼系数为5 000 N·s/m时,如果若波浪圆频率小于2.2 rad/s,2种装置的效率非常接近,若波浪圆频率大于4.2 rad/s,则柱形浮子装置的效率略高。由此可知,对于不同形状的浮子之间,装置的转换效率的高低与波浪的频率或周期有关,在进行浮子设计时,可通过上述计算及分析结果,根据实际海域的波浪周期或频率的分布情况选择合适的浮子形状。
4 结论
本文基于线性规则波理论针对固定式点吸收波浪能发电装置进行研究,从振动规律及能量转换的角度,通过水动力计算,分析浮子的运动响应及装置的能量转换特性。通过计算和分析可知,在固定海域,点吸式波浪能装置的能量转换效率受浮子及PTO系统2方面因素的影响:
1)浮子影响装置的一级转换效率,即浮子从波浪中吸收能量的效率。浮子的设计应从浮子与波浪共振的角度考虑,使浮子的固有频率与波浪的谱峰频率相等或接近,以使浮子以最大的效率吸收波浪能量。
2)PTO系统影响装置整体的能量转换效率,包括吸收波浪能量的效率以及浮子向PTO系统输出能量的效率,相同波浪条件下,装置的转换效率随阻尼系数先递增后递减。PTO系统的阻尼特性应与装置随阻尼的能量转换特性相匹配,以使装置具有最优的能量转换效率。
[1]CLEMENTA,MCCULLEN P.Wave energy in Europe:current status and perspectives[J].Renewable and Sustainable Energy reviews,2002(6):405-431.
[2]WHITTAKER T JT.Learning from the Islay wave power plant [C]//Proceedings of the 1997 IEE Colloquium on Wave Pow-er:An Engineering and Commercial Perspective.London,UK,1997:156-227.
[3]Yu.Z,Jiang N D,Yu Y G.Power ouput of an onshore OWC wave power station at Dawanshan island[C]//Proceedings of the European Wave Energy Symposium.Edinburgh,England,1993:271-276.
[4]CLAESON L.Energi fran hacets vagor[M].Stokholm:En-ergiforskningsnamnden,1987:175-193.
[5]Ocean Power Technologies Ltd.Making Waves in Power.[EB/OL].[20140406〛.http://www.oceanpowertechnolo-gies.com.2009.
[6]RHINEFRANKA K,AGAMLOHA E B.Novel ocean energy permanentmagnet linear generator buoy[J].Renewable En-ergy,2006,31:1279-1298.
[7]ERIKSSON M,ISBERG J,LEIJON M.Hydrodynamicmod-elling of a direction drive wave energy convert[J].Interna-tional Journal of Engineering Science,2005,43:1377-1387.
[8]吴必军,盛松伟,张运秋,等.复杂圆柱型波能装置能量转换特性研究[J].哈尔滨工程大学学报,2010,31(8):1023-1028.
[9]戴遗山,段文洋.船舶在波浪中运动的势流理论[M].北京:国防工业出版社,2008:36-84.
Research on the power characteristics of a point absorber
YANG Yunong1,XIE Peng2,ZHENG Xiongbo2
1.College of Power and Energy Engineering,Harbin Engineering University,Harbin 150001,China 2.College of Science,Harbin Engineering University,Harbin 150001,China
The paper dealswith a fix-pointed wave energy absorber and converter(WEC),based on the linearwave theory.Themotion of conical and cylindrical configuration was analyzed under the damped and undamped wave conditions.The interaction ofmotion response and energy conversion efficiency with geometry of the device,wave frequency and PTO systematic damping is investigated to clarify the optimizationmethod ofWEC design.The study carried out the conclusion thathow configuration of a proposed PTO system influences its energy conversion efficien-cy.The findings could provide a reference for future research and engineering application of pointed WEC.
point absorber;wave energy converter;ocean energy;PTO system;energy conversion efficiency
TK89,U661.32
A
1009-671X(2015)02-075-04
10.3969/j.issn.1009-671X.201406016
2014-06-27.
日期:2015-03-25.
中央高校基本科研业务费专项基金资助项目(HEDCFD1414)
杨雨浓(1994-),男,本科;
郑雄波(1978-),男,讲师.
杨雨浓,E-mail:yangyunonghrbeu@163.com.
http://www.cnki.net/kcms/detail/23.1191.U.20150325.0854.003.html

