秩估计及向量广义线性模型在风险投资中应用

王洪礼，姬晓鹏(天津大学管理与经济学部，天津300072)

秩估计及向量广义线性模型在风险投资中应用

王洪礼，姬晓鹏
(天津大学管理与经济学部，天津300072)

摘要:从风险投资案例中整理发现内在变化规律，有助于把握投资方向和路径。以2001—2011年全球投资公司每轮平均投资数据为例，由于数据不具备正态性和方差齐次性，基于秩估计方差分析，结果表明，各年之间均值存在显著差异。假设平均投资服从伽玛分布，其形状参数和尺度参数是年份的二次函数，基于向量广义线性模型估计各参数。最后预测2015年伽玛分布形状参数为1.195 9，尺度参数为5 816.186。风险投资位于任何区间的概率都可以通过分布函数计算。

关键词:风险投资;均值检验;秩估计;向量广义线性模型

风险投资是追求高额回报的资本投资，主要用于支持刚刚起步或尚未开始高新技术企业或高新技术产品。对于欧美发达国家而言，高新技术企业对于国民经济增长的贡献率从开始的5%～20%，慢慢上升到50%，目前已经高达60%～80%。其对经济的推动发展已经远远超过传统的资本密集型企业。

高新技术产业是高投资、高收益和高风险的事业。发达的风险资本网络通过降低进入一个行业的困难，为企业家提供了巨大的激励机制。风险资本家用他们的经验和他们之间的接触，减少了许多信息和机会中与新业务信息相关的耗费［1］。

根据2010年《中国创业投资及细目股权投资市场回顾》，在中国，新筹集的风险资本总数达到111.69亿美元，与2009年相比增长90.7%，新成立的风险投资基金为158家，与2009年比增长了68.1%。另一方面，投资项目与投资金额的大数量，带来了对即将初次公开发行公司之间激烈的竞争。因此，市盈率的倍数变得越来越大。从风险投资案例中整理发现内在变化规律，有助于明确投资方向和高新企业。

一、数据探索性分析

从Thomson Reuters旗下SDC platinum数据库导出2001—2011年部分指标数据。为了更好了解风险投资公司在每轮投资中的表现，选取投资公司每轮平均投资(Firm's Avg Company Investment)指标。在某轮投资中，风险投资公司可以投资好几个高新企业，对于不同高新企业，投资额度肯定有所不同。Firm's Avg Company Investment就是其平均值，单位为1 000美元。数据跨度为2001—2011年，剔除缺失数据后。2001年案例最多，有20 000多轮次投资，2009年案例最少，只有14 000多轮次投资。主要受美国次级债危机的影响，风险资本也大幅缩水。

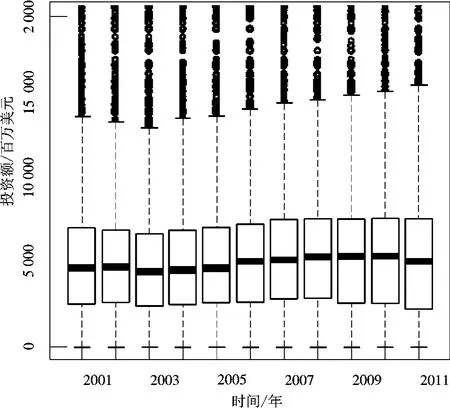
图12001　—2011年全球投资公司每轮平均投资盒子展示

图1盒子展示2001—2011年全球投资公司每轮平均投资。盒子中间粗线表示中位数，盒子底线和顶线分别表示25%和75%分位数。底线向下虚线延伸到最小值，顶线虚线延伸至1.5倍75%分位数，超过该值，视为异常值，用圆圈表示。每年每轮投资额度大概在500万美元，也有部分著名风险投资公司对于一家高新企业超过1 500万美元，投资金额大的异常值容易出现。从中位数来看，2001—2012年略微有增长的趋势。

为了更好地看出投资数据变化规律，计算出更详细的统计量(见表1)。基本每年的最小值为4 200美元，2010年的最小值为12 600美元。最小值涉及到的投资公司不具有普遍的含义。每年的25%经验分位数在25万美元左右，中位数在500万美元上下，75%经验分位数从700万慢慢增长到800万左右。最大值从1 000万递增到7 000万，2010—2011年最大值激增为7 000万，而以前的最大值在3 000万多一点。说明2010和2011年全球风险投资特别活跃，大规模投资随处可见。每年均值在600万美元左右，变化幅度不大。标准差表示波动的程度，每年标准差在800～900万美元之间，波动比较剧烈的是2010年，达到1 100万美元。偏度衡量数据是否关于均值对称，偏度接近零，说明数据对称性好。偏度越大于零，说明数据更容易出现比均值大的值，反之依然。2001—2009年偏度在10多个点，而2010—2011年偏度达到42和36，其大额风险投资频率更高。正态分布峰度为3，如果峰度大于3，就是所说的“尖峰厚尾”现象，表示大值更容易出现。每年峰度都远远超过3，“尖峰厚尾”现象非常严重。

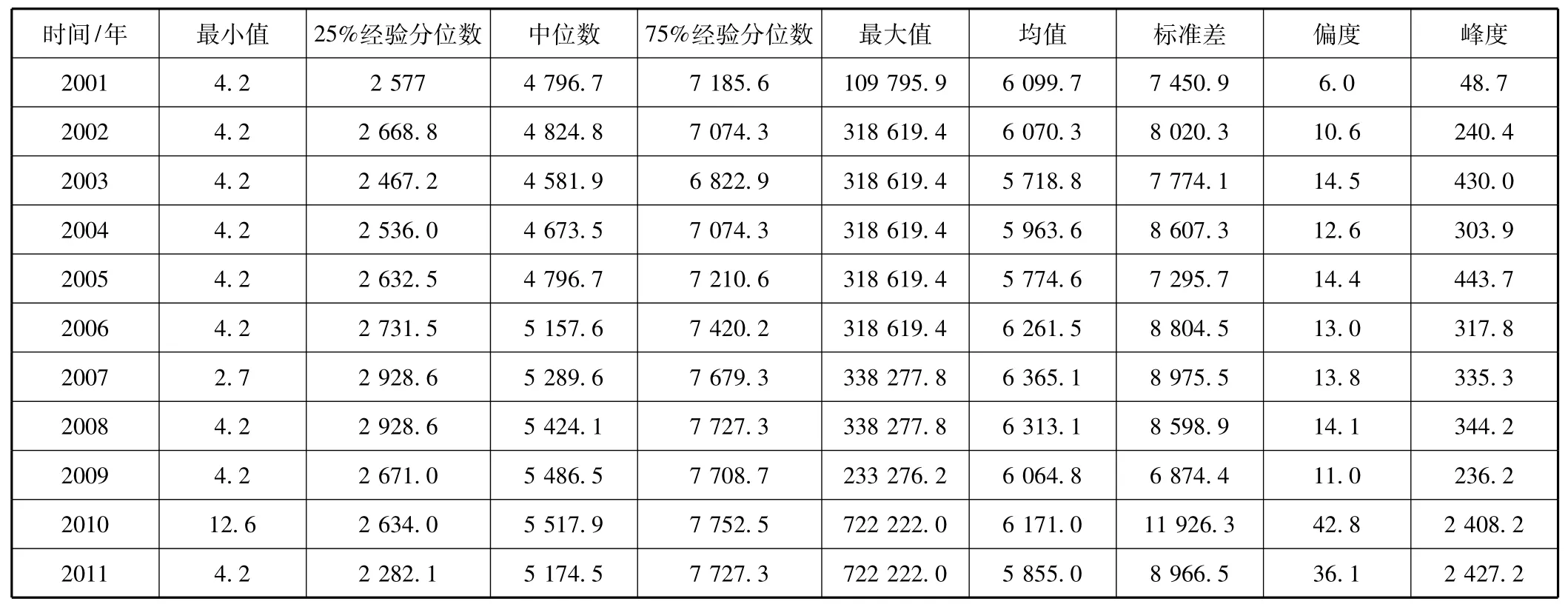
表12001　至2011年全球投资公司每轮平均投资基本统计量

一般模型都要求数据服从正态分布，可以利用正态性检验判断是否服从正态分布。正态性检验有很多，按照SAS和SPSS的规定，当样本量小于5 000时，以Shapiro-Wilk(W检验)为准。而当样本量大于5 000时，以Kolmogorov-Smirnov(D检验)为准。本文每年数据都远超5 000，采用Kolmogorov-Smi rnov D检验。每年检验结果都是一样的，D统计量达到极限值1。相伴概率小于0.05，拒绝原假设。2001—2011年全球投资公司每轮平均投资不服从正态分布。

二、秩估计的均值检验

一个关心的问题是全球投资公司每轮平均投资每年均值是否一致，常用的分析方法是方差分析表(analysis of variance，ANOVA)，但是ANOVA要求数据服从正态分布，而且不同年份方差相等［2］风险投资数据都不符合。本文选用基于秩估计的均值检验方法。该方法是一种非参数方法，对数据分布类型和方差没有要求。

基于秩次的估计方法相比于传统的最小二乘或者极大似然估计更健，不易受异常值影响。它是一种非参数方法。基于秩次的回归首先由Jurecková1971［3］Jaeckel 1972［4］提出。McKeanandHettmansperger 1978［5］提出的Newton递归优化算法将秩估计的计算量降低到可以接受的水平。从此之后，关于线性模型的秩推断按照传统最小二乘估计的框架建立起来。秩估计的权威专著见Hettmansperger and McKean 2011［6］。各种有关秩估计的诊断方法都相继被提出［7］。

由于每年风险投资案例个数不相同，本文数据就是一种完全随机试验。假设每个风险投资案例都是独立的，不同年份投资案例分布最多只是位置参数不同，分布类型和其它参数不会改变。

R语言的Rfit宏包对于单参参均值相等检验提供一种分散降低检验。同时给出调整之后的多重比较检验相伴概率。函数oneway．rfit完成检验。相伴概率小于0.05，拒绝原假设，认为11年均值之间存在显著差异。

表2是tukey方法修正之后的多重比较检验结果，置信下限和上限是两年组间均值之差的95%置信区间，如果该置信区间不包含零点，说明这两年均值存在显著差异。反之，如果该置信区间包含零点，认为这两年均值不存在显著差异。从表1中可以看出，2001年和2002年均值可以认为没有差别，2002年明显高于2003年，2003年低于2004年，2004年低于2005年，2005年低于2006年，2006年低于2007年，2007年和2008年没有差别，2008年和2009年没有差别，2009年和2010年没有差别，2010年高于2011年。

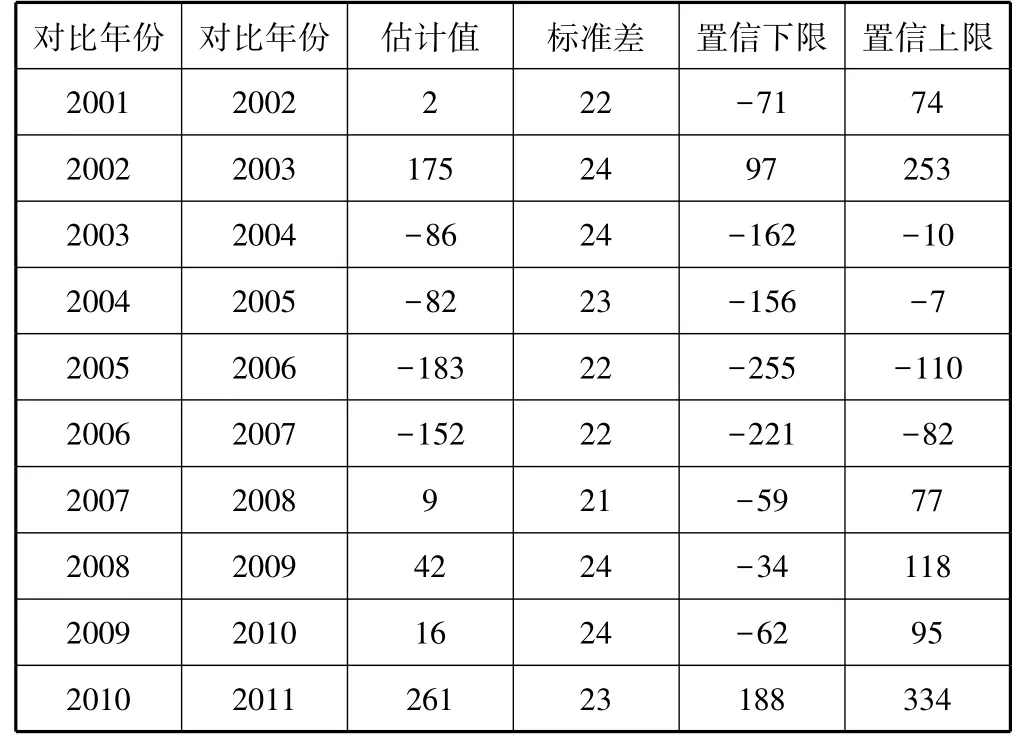
表2　2001—2011年全球投资公司每轮平均投资均值秩回归tukey修正多重比较检验

三、向量广义线性模型拟合伽玛分布

2001—2011年全球投资公司每轮平均投资均值存在差异，但是每一年份数据可以假定独立同分布。不同投资公司之间的投资应该具备一定的独立性，虽然同一投资公司不同的的投资案例可能具有一定的相关性，但是本文绝大部分数据是不同投资公司案例，满足独立性条件。进一步假设服从相同的分布。不同年份之间数据假设服从相同的分布类型，但是参数存在差异。

由于分布类型成千上万，选择哪种分布拟合是首选面临的问题。从正态性检验结果来看，全球投资公司每轮平均投资不符合正态分布，更符合伽玛分布。

伽玛分布有两个参数，形状参数α＞0和尺度参数μ＞0。随着参数不同，概率密度函数可以单减，也可以具有单峰，单峰两边的凹凸性还可以改变。

假设2001—2011年全球投资公司每轮平均投资案例相互独立且服从伽玛分布，每年之内案例伽玛分布参数相同，不同年份案例参数随时间而变。即形状参数α和尺度参数μ都是年份t的函数。根据均值建议的结果，均值有升有降，假设二次函数更合理。

传统线性模型假设响应变量服从正态分布，其均值是解释变量的线性函数，但是方差保持不变。广义线性模型允许响应变量概率分布为指数分布族中任何一员，其均值和解释变量的线性组合通过连接函数关联。但是响应变量只能有一个，而向量广义线性模型可以推广到多个响应变量。

向量广义线性模型由奥克兰大学统计系教授Yee2003［8］提出，经过不断改进，2008年形成R语言的宏包VGAM［9－11］可以看成向量广义线性模型的一种特殊情形，除了指数分布族，向量广义线性模型假定响应变量概率分布类型更多，如伽玛分布、Dagum分布等。除了分布类型的扩展，广义线性模型只是假设响应变量分布均值是解释变量的函数，向量广义线性模型假定多个参数是解释变量的函数，而不单单只是均值。这也是向量的解释。类似广义线性模型，参数和解释变量也是通过连接函数关联。所以本文的最终模型就是

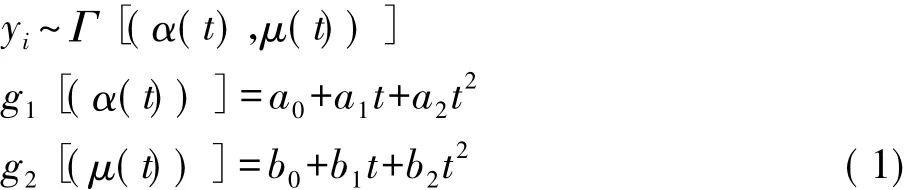
式中:yi为投资公司每轮平均投资;t为年份;g1和g2为连接函数。

本文两个参数的连接函数都取自然对数。

采用R语言VGAM宏包的vglm函数极大似然估计参数，经过9次循环终止，最大对数似然函数－1 904 306，自由度393 550。极大似然估计参数如表2，其中a表示形状参数α的系数，b表示尺度参数μ的系数。从表2可以看出，二次系数都为负值，表明抛物线开口向下，说明形状参数和尺度参数既有上升，也有下降。这点和样本数据经验分析吻合。所有参数估计标准误都比较小，说明估计量的波动范围小，是有效估计。

根据估计系数，令年份t=15，代入

0.294 4+0.026 8 x 15－0.002 3 x 152=0.178 9

计算2014年伽玛分布形状参数对数为0.178 9，尺度参数对数为8.668 4。指数得到原始形状参数为1.195 9，尺度参数为5 816.186。由于本文伽玛分布尺度参数就是其均值，所以2015年全球投资公司每轮平均投资600万美元，这和前些年数据的样本均值基本吻合。

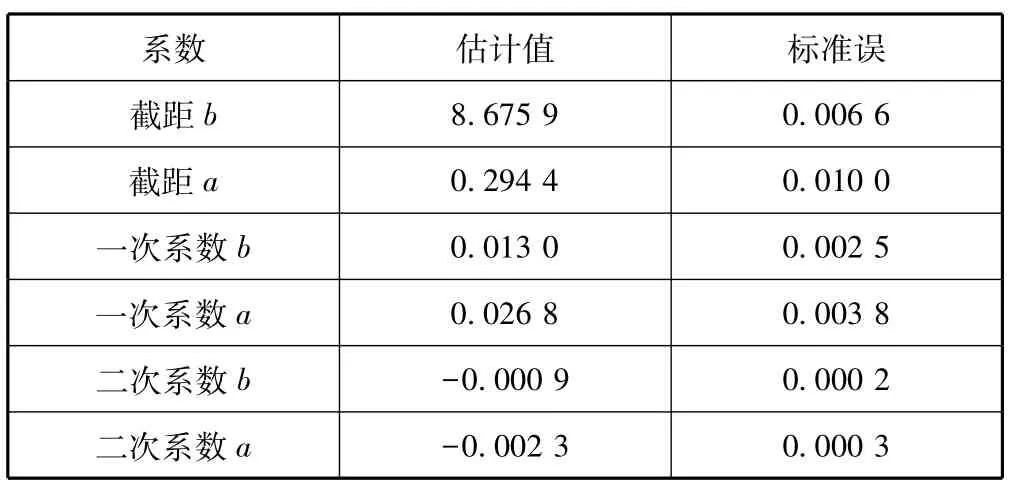
表2　伽玛分布向量广义线性模型参数极大似然估计

四、结语

本文基于全球风险投资案例数据，重点分析全球投资公司每轮平均投资。样本数据从2001—2011年。假设投资案例之间相互独立且服从伽玛分布，基于秩估计的单参数方差分析得到各年均值存在显著差异。认为各年案例伽玛分布参数是年份的二次函数，通过向量广义线性模型估计参数。最后预测2015年伽玛分布形状参数为1.195 9，尺度参数为5 816.186。估计2015年全球投资公司每轮平均投资在600万美元左右。投资额度在任何区间的概率都可以通过分布函数计算，有利于相关人士对全球风险投资的整体把握和认识。

参考文献:

［1］葛培初．美国在华风险投资及其对我国风险投资的启示［D］．苏州:苏州大学东吴商学院，2013．

［2］Welch B L．On the comparison of several mean values:An alternative approach［J］．Biometrika，1951(38):330-336．

［3］Jureckova J．Nonparametric estimate of regression coefficients［J］．The Annals of Mathematical Statistics，1971，42 (4):1328-1338．

［4］Jaeckel L A．Estimating regression roefficients by minimizing the dispersion of the residuals［J］．The Annals of Mathematical Statistics，1972，43(5):1449-1458．

［5］Mckean J W，Hettmansperger T P．A robust analysis of the general linear model based on one step R-estimates［J］．Biometrika，1978，65(3):571-579．

［6］Hettmansperger T，McKean J．Robust Nonparametric Statistical Methods［M］．New York:CRC Press，2011．

［7］王彤，鲍彦平．一类基于秩次的稳健线性回归估计与诊断方法［J］．数理统计与管理，2008(5):857-863．

［8］Yee T W，Hastie T J．Reduced-rank vector generalized linear models［J］．Statistical Modelling，2003(3):15-41．

［9］Yee T W，Stephenson A G．Vector generalized linear and additive extreme value models［J］．Extremes，2007(10):1-19．

［10］Yee T W．The VGAM package for categorical data analysis ［J］．Journal of Statistical Software，2010(32):1-34．

［11］Yee T W．Reduced-rank vector generalized linear models with two linear predictors［J］．Computational Statistics and Data Analysis，2014(71):889-902．

Application of Rank Estimation and Vector Generalized Linear Model in Risk Investment

Wang Hongli，Ji Xiaopeng
(College of Management and Economics，Tianjin University，Tianjin 300072，China)

Abstract:It's very important to find the rule of inherence and internal relationship from the case of risk investment，then venture capital investors can see clearly of the investment trend as well as the regarding detailed information．Take，for instance，the data of average investment amount of all the funds in the world follows neither the normality assumption nor the homogeneity of variance．We used“analysis of variance estimation of rank”to prove the significant difference of average investment by each fund among each year．Assuming the average investment follow the rule of Gamma distribution，and the form parameter and scale parameter are quadratic function of year parameter，we can estimate each parameter based on model of generalized linear vector．Finally we forecasted the form parameter of Gamma distribution of 2015 is 1.1959，and scale parameter of Gamma distribution of 2015 is 5816.186．The probabiting of the investment in any interval can be calculated by distribution function．

Keywords:venture investment;mean equality test;rank estimation;vector general linear model

通讯作者:姬晓鹏，18602108681@163．com．

作者简介:王洪礼(1945—)，女，教授．

收稿日期:2014-07-09．

中图分类号:X730

文献标志码:A

文章编号:1008-4339(2015)01-006-04