高边坡工程有限元正分析模型

闵江涛　马晨原

摘 要 本文探讨了有限元正分析的概念、基本原理、模型的建立和求解设计，并以某高边坡工程为研究对象，对其本构模型、屈服准则和力学参数等的选择进行设计，建立了高边坡工程的ANSYS三维有限元正分析模型。

关键词 高边坡工程 有限元法 正分析模型

中图分类号：TU457 文献标识码：A   DOI：10.16400/j.cnki.kjdkx.2015.04.013

High Slope Engineering Finite Element Analysis Model

MIN Jiangtao[1]， MA Chenyuan[2]

（[1] School of Hydraulic Engineering， Yangling Vocational & Technical College， Yangling， Shaanxi 712100;

[2] Xi'an Thermal Power Research Institute Co.， Ltd， Xi'an， Shaanxi 710032）

Abstract This paper discusses the concept of finite element analysis and solution design to establish basic principles， models， and a high slope engineering for the study， its constitutive model， yield and mechanical parameters such as selection criteria were designed to establish high dimensional finite element analysis model ANSYS  Positive Analysis Model.

Key words high slope; engineering; finite element; positive analysis model

0 引言

有限元法①是一种把物体或结构整体所具有的域（V）划分为有限多个被称为单元的子域（Vn），以求得近似解的一种数值计算方法。有限元分析法的基本思想是用较简单的问题替代较复杂的问题来求解，在20世纪50年代，它是应用在流体力学领域中的一种有效的数值分析方法，并在其他工程领域得到迅速发展。

1 有限元正分析模型研究

1.1 有限元法的基本原理

有限元法的基本原理是将要进行分析的连续力学介质，假想地划分成由有限个小单元组成的组合体，而这些小单元仅在结点处有力的连接。在有限元分析中，基本未知量一般是结点位移分量，采用分块近似的思想，通过假设的形函数建立起结点位移和单元内任一点位移间的相互关系;其次，采用几何方程，通过单元内任一点位移与应变间的几何关系的建立，按照物理方程确定单元内任一点的应力与应变关系;最后，按照平衡方程确定应力与结点力的作用关系，再确定单元结点位移与结点作用力之间的相关关系，随着结构里网格划分的越来越细，将形成越来越多的单元数目，解的精确度也会不断提高，最终得到精确解。

1.2 有限元模型的建立

采用有限单元法时，因岩土边坡工程的稳定分析问题多是力和强度关系问题，不太考虑岩土体材料的软化及硬化，通常选用理想的弹塑性模型来分析，通过将弹塑性有限元分析和极限平衡法分析结果进行对比，结果显示二者的一致性较好，选取强度准则条件也较严格，并且所选择的计算参数都比较接近实际，使得计算方法的可靠性可以得到保证。

1.2.1 确定材料性质的基本假定

弹塑性材料是介于塑性和弹性之间的，采用下面三个基本假定：②（1）材料在初次屈服达到之前是各向同性、均质和连续的;（2）体积变化和平均应力间呈线弹性关系，由于塑性变形部分的体积变化很小，可以忽略不计;（3）不考虑变形的速度、温度、回弹、蠕变等因素对应力、应变的影响。

1.2.2 选取本构模型和力学参数

岩土体本构关系，就是其应力与应变之间的关系。通过结合试验分析与现场测试结果，由岩土体材料自身特性所决定，用数学模型来描述来岩土体间的应力与应变关系，根据力学特性建立起本构模型。③Drucker-Prager弹塑性模型反映剪切作用引起的胀容性质，其考虑静水效应的作用影响，并且模型光滑无尖点，它反映了材料自身的塑性变形，因而在岩土体材料的弹塑性模拟计算中得到广泛应用。Drucker-Prager屈服准则中屈服面与材料的屈服变化无关，不会发生屈服变化，故没有强化准则。其屈服强度与侧限静水压力成正比，其塑性行为被假定为理想弹塑性，而且此材料还考虑了屈服带来的体积膨胀影响，如图1所示。

图1 D-P材料的屈服面示意图

本文的弹塑性材料选取D-P屈服准则，故在求解计算中需要输入的D-P材料参数：如弹性模量、泊松比、内摩擦角、粘聚力和膨胀角。实践应用表明，膨胀系数 =  = 0.8时，与实际情况较相符，并且随着膨胀角的增大，边坡的稳定安全系数也将随之增大。

1.3 有限元模型的求解设计

有限元法求解的基本思路是将原有的连续体结构用有限个单元构成的离散化结构代替，这些离散化后的单元体仅在结点处存在力的联系。ANSYS有限元分析法的基本过程可以归纳为化整为零—分片近似—单元分析—集零为整—方程求解—计算分析。

（1）定义问题和求解域。在求解分析有限元时，应先明确研究对象，对求解域的物理性质和几何区域进行计算，这是由实际求解的具体问题决定的。边界范围的选取对有限元计算结果影响较大。在有限区域内进行离散处理分析时，为了不产生较大的误差应当选取足够大的计算范围。

（2）结构离散化。连续问题离散化是将连续结构剖分成具有不同大小和形状且彼此相连的有限个单元与结点组成的离散域，单元仅在结点处连接，并且单元之间的相互作用仅通过结点来进行传递。

（3）单元结构分析。单元和结构分析是有限单元法分析基础。在基于单元分析的基础上进行结构的离散化处理，总结出几何形状都相似的单元的共性和结构的力学性质，这使得对于结构的分析必须通过单元分析，再设计合适的近似解。

（4）边界条件。在施加边界约束时，要保证在一定的荷载作用下结构体不产生整体刚性变形，位移值要能够唯一的确定。如规定分别代表方向上的位移时，在三维有限元分析中，位移边界条件取模型的4个侧面为法向约束，底面为铰支约束，坡面为自由滑动面，即为底面3个方向都约束，即===0。总之要根据实际工程情况合理选择边界条件。

（5）求解处理与结果评价。有限元分析可分为前处理步、求解处理步及后处理步三步。在前处理中进行有限元实体模型的建立与网格的剖分;通过求解处理来计算方程组的解;在后处理中以图形、表格等方式来显示计算结果，以便直观、简便地获取信息。

2 工程实例

2.1 某高边坡工程地质条件及变形测点设置情况

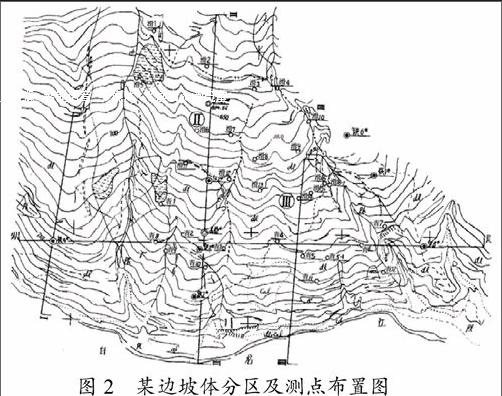
某高边坡体④位于白龙江与让水河交会的左岸处，坡体面积约2km2，呈一“喇叭形”地貌。在1986年设置了边坡体监测网，监测网根据边坡体的地质地貌特征和冲沟切割情况，将边坡体划分为3个区，如图2所示。其中Ⅲ区地形较缓，坡度大致为20€皛25€埃旅娼贤暾8们菹虺？70m、宽250m，根据打孔试验确定，发现自坡顶向下40.50m～45.50m之间存在厚度为5.0m的粉质粘土层。

2.2 边坡体有限元模型的建立

根据前面所介绍的工程具体特点，以Ⅲ区域为研究对象建立边坡体ANSYS三维有限元简化模型，并考虑边坡体材料为弹塑性，选用D-P本构模型进行分析，其中，膨胀角取为 = 0.8。边坡计算范围按以下标准选取：

为消除边界的影响效应，将边坡向左右各延伸285 m，即取坡顶到右端边界的距离是285m，坡脚到左端边界的距离是285m，均相当于坡高的1.5倍;岩基的深度取1倍坡高，即上、下边界总距离为380m。其中，坡顶向下40.50m～45.50m之间存在厚度为5.0m的粉质粘土层。

图2 某边坡体分区及测点布置图

模型采用三维局部坐标系，以地质概化模型左端边界与延伸基础交界上游端为坐标原点，轴正方向指向垂直于河谷，轴正方向铅直向上，轴正方向指向河谷下游且平行河谷，对该边坡体结构进行建模分析。几何模型建立范围为：方向垂直河谷向山内侧延伸至900 m;方向，从下边界一直延伸至自然坡面，最大高程至380m，上、下游方向，以白龙江流向延伸50 m。计算区域的岩基底部采用铰支约束，岩基左、右两侧采用法向约束，岩体段纵向也采用法向约束，坡面为自由边界。

ANSYS计算的荷载按边坡体结构的自重荷载考虑，其中，地下水位以上的岩体按天然容重考虑，地下水位以下的岩体按饱和容重考虑。定义单元采用四面体Solid45单元，根据映射网格法剖分网格。对该边坡结构进行地质概化处理后，所得边坡地质概化模型如图3示。

图3 边坡体地质概化模型

3 总结

（1）本文对有限元法的概念、基本原理、模型的建立和求解设计进行了系统探讨。（2）结合某高边坡工程实例，通过对其地质结构的概化处理，建立了该高边坡的ANSYS有限元正分析模型，下一步可以通过求解计算，确定该边坡体岩体力学参数与变形位移量之间的相关关系。

注释

① 荣先成.有限元法[M].成都：西南交通大学出版社，2007：48-58.

② 谢定义，徐干成.岩土材料弹塑性动本构模型研究概括[J].岩土力学，1993.14（3）：81-86.

③ 周建方，朱俊高.邓肯E-v模型与E-B模型的比较[J].水利水电科技进展，2008.28（1）：4-7.

④ 杨杰，伍美华，陈平志等.碧口水电厂大坝安全监测资料分析报告[R].西安：西安理工大学，2007.