基于稀疏表示和最小二乘回归的基因表达数据分类方法

简彩仁， 陈晓云

(1. 福州大学数学与计算机科学学院, 福建 福州 350116； 2. 厦门大学嘉庚学院， 福建 漳州 363105)

基于稀疏表示和最小二乘回归的基因表达数据分类方法

简彩仁1, 2， 陈晓云1

(1. 福州大学数学与计算机科学学院, 福建 福州 350116； 2. 厦门大学嘉庚学院， 福建 漳州 363105)

提出基于稀疏表示和最小二乘回归的分类方法： 用训练样本重构测试样本， 先利用稀疏表示剔除噪声样本， 接着用最小二乘回归和最近邻子空间准则对样本分类， 可以克服传统分类方法存在的过拟合问题. 在6个基因表达数据上的实验结果表明, 该方法可以提高分类准确率.

稀疏表示； 最小二乘回归； 基因表达数据； 分类

0 引言

中国每年新发肿瘤病例约为312万例， 平均每天有8 550人， 每6 min就有一个人被确诊为癌症[1]. 伴随着生活水平的提高， 人们更加关心自己的健康， 渴望战胜各种恶性肿瘤. 肿瘤不能等同于癌症， 肿瘤可以分为良性肿瘤和恶性肿瘤， 后者才称为癌症. DNA微阵列技术可同时测量成千上万的基因表达水平的高通量性为癌症诊断提供了支持[2]. 通过对DNA芯片测定的基因表达数据建立有效的分类模型， 可以在分子水平上实现对肿瘤类型的准确识别， 对癌症的诊断和治疗具有重要意义[3].

肿瘤样本的分类最大的挑战是基因表达数据的小样本高维数特征， 通常样本的个数几十到几百个， 而基因数量却往往超过一千， 甚至达到几万. 在过去的十几年， 许多肿瘤基因的分类模型已经被提出. Paul等[4]采用一种投票策略对基因表达数据进行分类， 该方法优于AdaBoot等方法[4]， Bolón-Canedo等[5]利用C4.5， 朴素贝叶斯分类器等组合分类器对基因表达数据进行分类， 实验证明可以提高单种分类器的分类精度. 杨帆等[6]用随机森林的潜在k近邻算法对基因表达数据分类也证明了有效性， 更多的基因表达数据分类方法可以参见文[7]. 但是这些传统方法存在训练阶段和测试阶段， 容易出现过拟合问题.

稀疏表示是一种基于L1正则化的高效的数据表示方法， 已经成功应用在LASSO和压缩感知等领域.

通过稀疏表示， 可以用训练样本来表示测试样本， 利用L1范数的稀疏性质构建基于稀疏表示的分类器(SRC). 有别于传统的有监督学习方法， 用训练样本训练分类器， 再用分类器对测试样本进行分类， SRC没有训练阶段和分类阶段， 因此在一定程度上可以克服过拟合问题. SRC已经成功应用在人脸识别[8]和肿瘤分类[9]. Zheng等[10]提出MSRC通过训练样本的每个类别计算meta样本再用SRC方法进行分类. Li等[11]提出NNLS采用非负最小二乘回归构建的分类方法也用了类似的思想. 训练样本中可能有噪声样本， 这些样本会影响分类的结果， 而SRC、 MSRC和NNLS没有考虑噪声样本对分类结果的影响.

受上述研究的启发， 针对这些方法的不足之处， 提出基于稀疏表示和最小二乘回归的分类方法： 用训练样本重构测试样本， 先利用稀疏表示剔除噪声样本， 接着用最小二乘回归和最近邻子空间准则对基因表达数据分类.

1 相关工作

1.1 最小二乘回归

假设ym×1是未知类别标签的基因表达数据样本，Xm×n是已知类别标签的基因表达数据样本训练集， 有n个训练样本，m个基因属性， 其中m>>n， 用已知类别标签的训练集表示未知类别标签的样本

其中:Xi为第i个训练样本， 因为m>>n， 是一个超定方程， 求解公式(1)的精确解是没有意义的. 本文考虑如下的最小二乘回归模型

假设O(w)为问题(2)的目标函数， 则

tr(X)表示求迹， 这里应用了tr(X)=tr(XT)和tr(XY)=tr(YX). 对X求导得到

令公式(4)为0， 得到

1.2 稀疏表示

稀疏表示用尽可能少的基函数近似稀疏叠加表示一个新的信号. 求解w的稀疏问题为

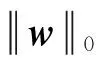
第二届全国青年工程风险分析和控制研讨会简讯 李典庆，曹子君，张洁，张璐璐，郑文棠，朱鸿鹄，张华(140)

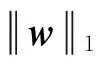
Kim等[12]给出了一种快速计算公式(8)的方法.

1.3 最近邻子空间准则

假设基因表达数据样本集有K个类别{l1,l2, …,lK}， 对一个基因表达数据样本y求解系数向量w， 对每一个类计算如下的度量余量

其中:δk(w):Rn→Rn计算得到类lk的系数， 其第j个元素定义为

最后， 样本y所属的类为

2 基于稀疏表示和最小二乘回归的两阶段分类方法

基于同类样本来自同一个子空间的假设， 稀疏表示分类方法(SRC)用训练样本重构测试样本， 训练样本中对测试样本重构的贡献小的样本可以视作测试样本的远邻样本， 这些样本可能与测试样本来自不同的类. 对含有大量噪声的基因表达数据， 远邻样本也可能是噪声样本. 因此， 远邻样本会影响分类的结果. 本节用稀疏表示剔除噪声样本， 并用最小二乘回归和最近邻子空间准则设计分类器分类.

寻找测试样本的噪声样本最直接的做法是计算两个样本之间的距离， 但是基因表达数据是高维数据， 在高维空间定义距离是不可靠的， 而且只考虑了两样本之间的距离关系， 忽略了其余样本的影响. 利用稀疏表示的稀疏系数可以克服这种缺点. 为了便于剔除噪声样本， 对稀疏系数加入非负限制， 考虑如下的非负稀疏表示模型.

算法:基于稀疏表示和最小二乘回归的两阶段分类方法(SRLSRC)Input:训练集Xm×n,测试样本y,训练样本类别ltrain,正则参数λOutput:训练样本类别ltestStep1:标准化训练样本集Xm×n和测试样本y的每个样本,使每个样本具有单位L2范数;Step2:解决问题(11)得到非负稀疏系数w,并剔除噪声样本,得到新的训练集Xnew;Step3:利用公式(5)求回归系数wnew=(XTnewXnew)-1XTnewy;Step4:最近邻子空间准则,即公式(9)和(10)分类,得到训练样本类别ltest.

3 实验分析

通过实验验证基于稀疏表示和最小二乘回归的两阶段分类方法(SRLSRC)的有效性， 对比方法有LSRC(最小二乘回归+最近邻子空间准则)、SRC[9]、MSRC[10]、NNLS[11]和传统的支持向量机(SVM)、 最近邻分类器(1-NN).

3.1 数据集描述

选用6个常用的基因表达数据集来验证SRLSRC的有效性， 数据来源于文献[13]详见表1.

表1 数据集描述

所有数据集都标准化为具有单位L2范数， 即用式(12)标准化:

其中:x表示一个样本.

3.2 实验结果及分析

对上述数据集采用十折交叉验证， 为了在统一的环境下实验， 采用GEMS系统[13]对数据集进行分组， 总共分为十组， 九组用于训练， 一组用于测试. 实验环境为Win7系统， 内存2 G， 所有方法(SVM除外)都用Matlab2010b编程实现. 各种方法的参数设置如下： SRLSRC、 SRC和MSRC的正则参数λ设置为0.01； SVM采用GEMS系统得到， 对于多类问题采用一对多(one versus rest， OVR)支持向量机实现， 采用线性核函数(根据文献[13]的研究这种设置的参数方法效果较为理想)； 1-NN方法采用matlab自带的knnclassify函数实现. 实验结果用分类准确率衡量如表2.

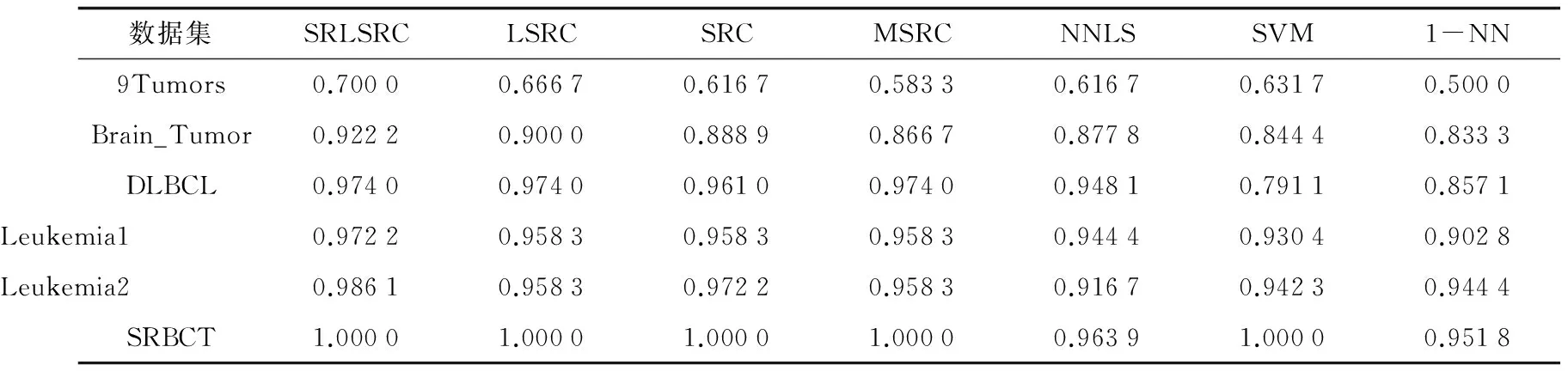
表2 分类准确率

从实验结果不难发现， SRLSRC的分类准确率是最高的， SRLSRC分类准确率高于SRC、 MSRC和NNLS， 这说明考虑剔除远邻样本可以提高分类准确率. SRLSRC、 SRC、 MSRC和NNLS的分类准确率总体高于传统的SVM和KNN， 这说明利用训练样本重构测试样本， 不存在过拟合问题， 可以提高聚类准确率.

传统方法的运行效率比较高， 本文对比用训练样本表示测试样本的方法， 即SRLSRC， LSRC， SRC， MSRC， NNLS等方法的运行时间， 结果如表3.

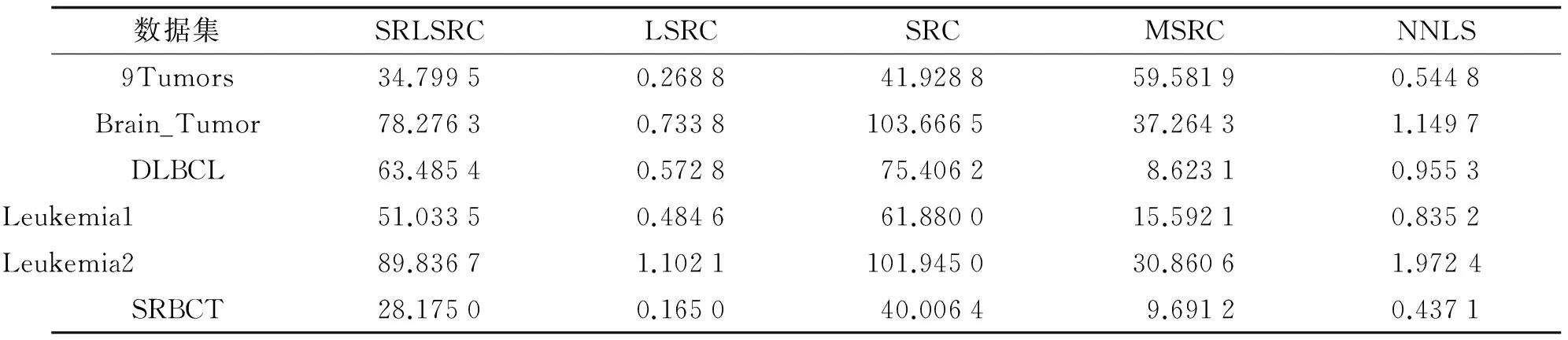
表3 不同分类方法运行时间对比

由表3可以发现， SRLSRC的运行时间开销比较大， 但是比SRC的运行速度更快， 在9Tumors数据集上， 比MSRC快. SRLSRC和SRC都存在求解稀疏表示的过程， 尽管SRLSRC比SRC多了最小二乘回归的计算步骤， 从LSRC的运行时间可以发现这一计算过程花费的时间较少， 主要的原因是限制w≥0加快了计算速度[12](本文应用l1_ls软件实现: https://www.stanford.edu/～boyd/l1_ls/). 此外当类别数多时， 运行效率也高于MSRC.

4 结论

本文提出的基于稀疏表示和最小二乘回归的两阶段分类方法(SRLSRC)可以提高基因表达数据的分类准确率. SRLSRC用训练样本来表示测试样本， 没有训练阶段， 因此不容易出现过拟合的问题； SRLSRC剔除噪声样本， 可以减少噪声样本对分类结果的影响. SRLSRC因为存在两个阶段， 其运行时间开销较大， 如何更高效地剔除噪声样本将在以后的研究中给出.

[1] 郝捷， 陈万青.中国肿瘤登记年报[M]. 北京： 军事医学科学出版社, 2012.

[2] Brown P O, Botstein D. Exploring the new world of the genome with DNA microarrays[J]. Nature Genetics, 1999, 21: 33-37.

[3] Pham T D, Wells C, Crane D I. Analysis of microarray gene expression data[J]. Current Bioinformatics, 2006, 1(1): 37-53.

[4] Paul T K, Iba H. Prediction of cancer class with majority voting genetic programming classifier using gene expression data[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2009, 6(2): 353-367.

[5]Bolón-Canedo V, Sánchez-Maroo N, Alonso-Betanzos A. An ensemble of filters and classifiers for microarray data classification[J]. Pattern Recognition, 2012, 45(1): 531-539.

[6]杨帆, 林琛, 周绮凤, 等. 基于随机森林的潜在k近邻算法及其在基因表达数据分类中的应用[J]. 系统工程理论与实践, 2012, 32(4): 815-825.

[7] Asyali M H, Colak D, Demirkaya O,etal. Gene expression profile classification: a review[J]. Current Bioinformatics, 2006, 1(1): 55-73.

[8] Wright J, Yang A Y, Ganesh A,etal. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227.

[9]Hang Xiyi, Wu Fangxiang. Sparse representation for classification of tumors using gene expression data[J]. Journal of Biomedicine and Biotechnology, 2009, doi:10.1155/2009/403689.

[10] Zheng Chunhou, Zhang Lei, Ng T Y,etal. Metasample-based sparse representation for tumor classification[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2011, 8(5): 1 273-1 282.

[11] Li Yifeng, Ngom A. Classification approach based on non-negative least squares[J]. Neurocomputing, 2013, 118: 41-57.

[12] Kim S J, Koh K, Lustig M,etal. An interior-point method for large-scale l1-regularized least squares[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 606-617.

[13] Statnikov A, Tsamardinos I, Dosbayev Y,etal. GEMS: a system for automated cancer diagnosis and biomarker discovery from microarray gene expression data[J]. International Journal of Medical Informatics, 2005, 74(7): 491-503.

(责任编辑： 林晓)

Gene expression data classification model based on sparse representation and least square regression

JIAN Cairen1, 2, CHEN Xiaoyun1

(1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116， China；2. Tan Kah Kee Colleage, Xiamen University, Zhangzhou, Fujian 363105， China)

A new classification method based on sparse representation and least square regression is proposed. The method first reconstructs a test sample by the training samples to remove noise samples by using sparse representation, and then it uses least square regression and subspace nearest rule to classify samples. The method can overcome the over fitting problem of the traditional classification methods. Experimental results on six gene expression data sets show that the proposed method can improve the classification accuracy.

sparse representation; least square regression; gene expression data; classification

2014-02-25

陈晓云(1970-)， 教授， 主要从事数据挖掘、 模式识别、 机器学习等方面研究， c_xiaoyun@21cn.com

国家自然科学基金资助项目( 71273053)

10.7631/issn.1000-2243.2015.06.0738

1000-2243(2015)06-0738-04

TP311; TP371

A