钨矿石磨矿动力学研究

鄢发明， 艾光华， 吴彩斌， 李晓东， 石志中， 毛文明

（1.江西理工大学江西省矿业工程重点实验室，江西 赣州341000；2.湖南柿竹园有色金属有限责任公司，湖南 郴州423037）

磨矿作业在选矿厂中占有非常重要的地位，其能耗约占整个选矿厂能耗的50%左右[1].磨矿是一个复杂的高能耗、低效率的作业，其过程还不是完全清楚，为了更好地进行磨矿作业，研究磨矿动力学很有必要[2-4].目前，对矿石磨碎的动力学模型有许多种，主要分为2类，一类是粒度及其相关量与时间及其相关量的动力学模型，另一类是总体平衡动力学模型[5].本文选用E.W.戴维斯提出的动力学模型来分析讨论钨矿石在磨矿过程中的行为，此模型研究的是被磨物料磨碎速率与其磨矿时间的关系，而物料的磨碎速率遵循磨矿动力学方程，磨矿动力学方程的参数k和n在一定程度上可以反映物料被磨碎的快慢以及为选择性磨矿和现场生产指标评价提供依据[6-15].磨矿动力学方程式还可以用来预测不同磨矿时间磨矿产品的粒度分布[16-18].在很多情况n阶磨矿动力学较一阶磨矿动力学更符合实际，因此大多情况下，此动力学模型均是用n阶磨矿动力学来分析矿石在磨矿过程中的行为[19-21]，而本文针对湖南柿竹园钨矿石特性，将其磨矿产品分为不大于0.1 mm粒级的细粒级产品和大于0.1 mm粒级的粗粒级产品，分别探讨其磨矿动力学规律并建立数学模型，为选矿厂磨矿实践提供指导.

1 试 验

1.1 矿石性质

试验所用钨矿石取自湖南柿竹园多金属选厂，主要矿物为白钨矿、黑钨矿、假象及半假象黑钨矿，其中白钨矿与黑钨矿的比例为7∶3.白钨矿密度为6.1 t/m3，解离度平行中等，普氏硬度系数f为4.5～5，属中等硬度；黑钨矿密度为7.30 t/m3，解离度平行完全，普氏硬度系数f为4～5.5，属中等硬度.钨矿石不规则抗压强度为400 kg/cm2左右，即换算成普氏硬度系数f为4左右.

1.2 试验条件

在XMB三辊四筒磨机上分别进行了钨矿石不同磨矿时间（2min、3min、4min、5min、6min、7min）的分批磨矿试验.所用磨筒尺寸为φ135mm×146mm，磨筒转速为85 r/min，磨矿介质为钢球，磨矿浓度为70%，介质充填率为45%，磨矿量为200 g.

1.3 粒度测定

采用筛孔尺寸为 0.074 mm、0.1 mm、0.15 mm、0.3 mm、0.5 mm、1.0 mm、2.0 mm 的套筛测定物料0.074～2.00mm间的各粒级分布；采用激光粒度分析仪测定物料≤0.074 mm的各粒级分布.

1.4 试验方法

对不同磨矿时间下的磨矿产品粒度分布，用一阶磨矿动力学进行验证，并采用Origin软件进行拟合，求解不同粒级下磨矿动力学参数k值，观察并比较求解不同粒级的磨矿动力学参数k值时的拟合程度R2，确定磨矿产品符合一阶磨矿动力学的粒级范围，并建立一阶磨矿动力学方程式[22-24].对于磨矿产品不在一阶磨矿动力学粒级范围内的，同样采用Origin软件进行求解不同粒级的磨矿动力学参数k和n值，并在此粒级范围内建立n阶磨矿动力学方程式[25].最后分别运用所求得的各自粒级范围内的一阶或n阶磨矿动力学方程式进行理论计算，将计算结果与实际磨矿结果进行比较，来验证本研究所求解的磨矿动力学方程式的准确性，为选矿厂磨矿提供理论依据[26-28].

2 磨矿动力学原理

磨矿动力学是指被磨物料的磨碎速率与磨矿时间的关系，其n阶磨矿动力学方程式为：

式（1）中：R为磨矿为t时刻磨矿产品中粗粒级产率；R0为原矿中该粗粒级比率；t为磨矿时间；k为动力学参数；n为动力学参数，当n=0时称为零阶动力学，n=1时称为一阶动力学[12，29].

对式（1）进行变换得：

式（1）中，动力学参数n和k分别是粒度d的函数，表达式如式（4）和式（5）所示[30]：

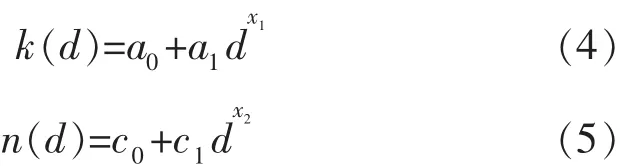
式（4）、式（5）中 c0，c1，a0，a1及 x1，x2分别为待定参数.

3 结果与讨论

3.1 一阶磨矿动力学

3.1.1 磨矿动力学参数k的求解

在磨矿条件为磨筒转速170 r/min，矿浆浓度为70%，介质充填率为45%下，依次对物料进行不同时长（2 min、3 min、4 min、5 min、6 min、7 min）的磨矿，结果如表1所示.

由表1可知，0.1 mm及其以下粒级筛上累积产率随着时间的延长逐渐减少，且趋势较平缓；0.1mm以上粒级筛上累积产率在5 min之前减少的较快，而5min之后减少的较慢.这表明粗粒级矿粒相对于较细粒级矿粒更好磨，随着磨矿时间的延长，各类粒级矿石裂缝、缺陷越少，磨细越困难，因而使得矿石的可磨性逐渐变差[8].

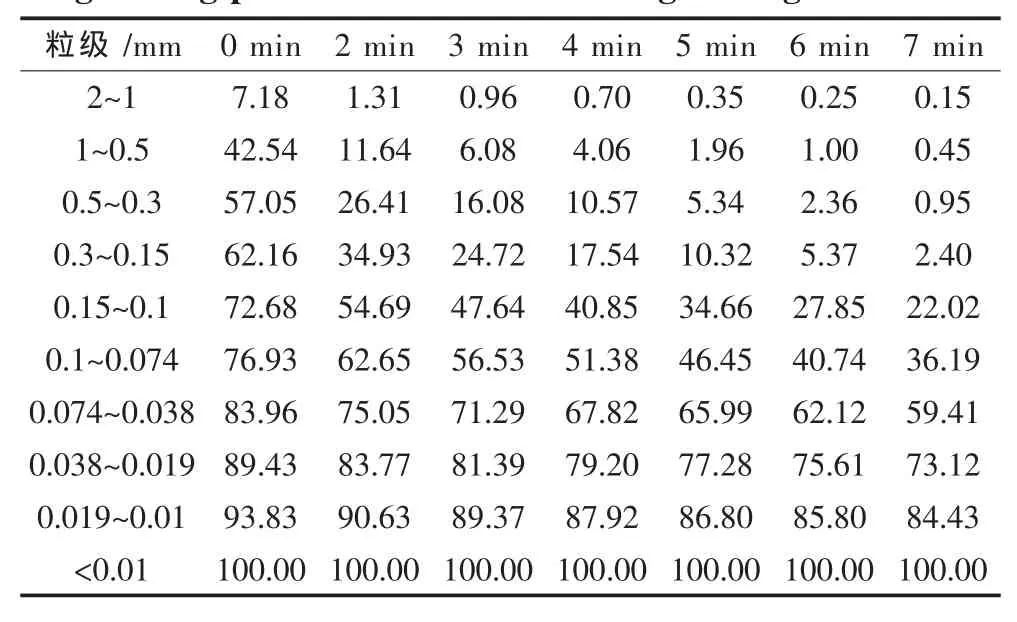
表1 不同磨矿时间下磨矿产品筛上累积粒度分布/%Table 1 Cum ulative oversize distribution of grinding products under different grinding tim e/%

由表1可计算出磨矿产品不同时间不同粒级的ln（R0/R）值，结果如表 2 所示.

表2 不同磨矿时间下不同粒级的ln（R0/R）值Tab le 2 ln（R0/R） of different particle sizes under different grinding tim e

根据表2绘制不同粒级的ln（R0/R）与时间t的关系曲线，如图1所示.并根据式（1）对不同粒级的ln（R0/R）与时间t的关系曲线进行线性拟合，得到钨矿石不同粒级下的磨矿动力学参数k值，结果如表3所示.

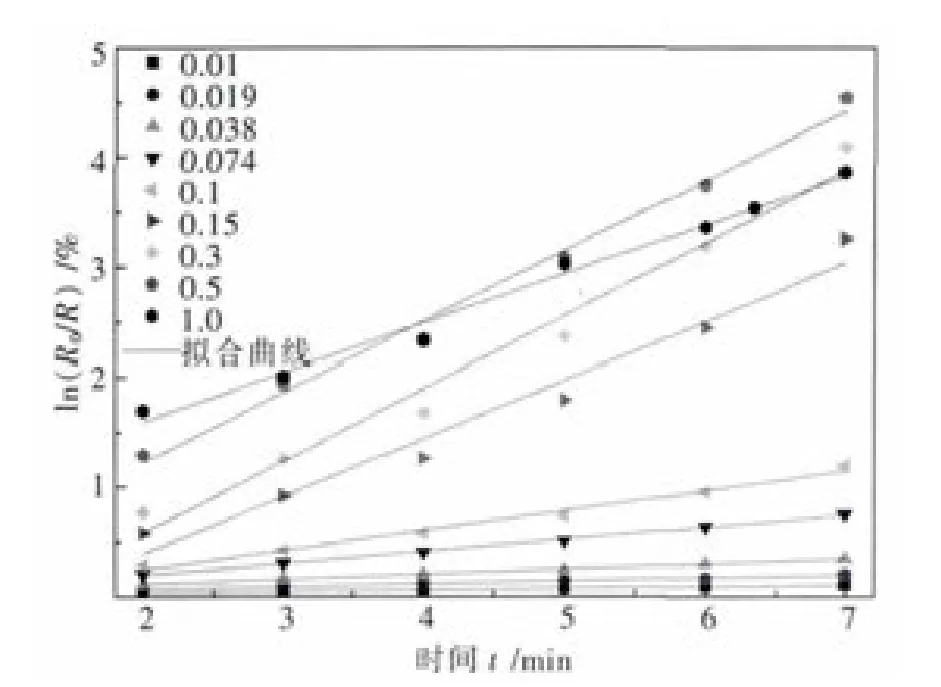
图1 不同粒级下ln（R0/R）与时间t的关系曲线Fig.1 Relationship curve between the ln（R0/R） values of different particle sizes and grinding tim e t

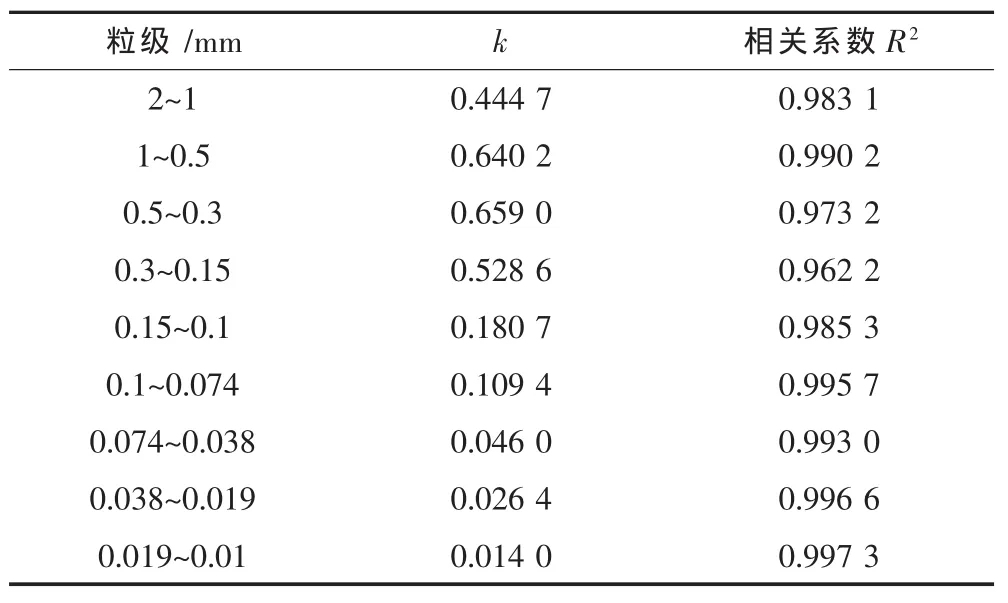
表3 不同粒级的磨矿动力学参数kTable 3 G rinding kinetics parameters k of different particle sizes

由表3可知：随着粒级的减小，k值逐渐变小，矿粒被磨碎速率越小[5]，这是因为随着矿石粒径的减少，剩余矿粒表面裂缝相对较少，强度较高.矿粒在0.1mm及其以下粒级的线性相关系数R2均在0.99以上，而在0.1mm以上粒级的线性相关系数R2均在0.96以上，拟合程度不高.因此矿粒在0.1mm及其以下粒级符合一阶磨矿动力学，而在0.1mm以上粒级则符合n阶磨矿动力学.

3.1.2 一阶磨矿动力学方程的建立

在上述基础上，将表3中不同粒级的磨矿动力学参数k在0.1mm及其以下粒级进行曲线拟合，求出钨矿石的磨矿动力学参数k的表达式，结果如图2所示.

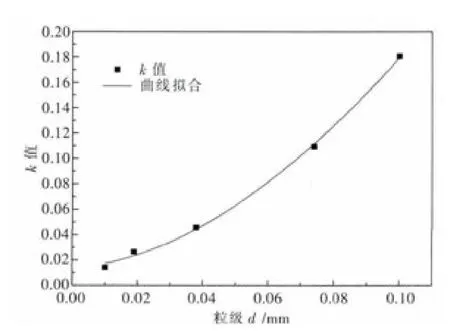
图2 磨矿动力学参数k与d的关系曲线Fig.2 Relationship curve between the grinding kinetics param eters k and d

由图2可知，参数Ki呈幂函数的形式，可表示为：

利用Origin软件对式（6）进行曲线拟合，求得参数a0、a1和x，从而求得钨矿石的一阶磨矿动力学参数k的表达式为：

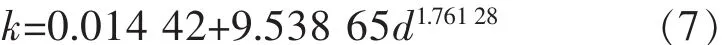
将式（7）代入式（1），可建立钨矿石在 0.1 mm 及其以下粒级的一阶磨矿动力学方程为：

3.2 n阶磨矿动力学

3.2.1 磨矿动力学参数n和k的求解

由上述分析可知，钨矿石在0.1 mm以上粒级时不符合一阶磨矿动力学.为验证其是否符合n阶磨矿动力学，由表1中0.1 mm以上粒级数据通过式（3）进行计算，得到不同粒级的lg（lg R0/R）与t的关系，结果如表4所示.

表4 不同磨矿时间下不同粒级lg（lg R0/R）值Tab le 4 lg（lg R0/R） of different particle sizes under different grinding tim e

根据表4绘制不同粒级的 lg（lg R0/R）与 lg t的关系曲线，如图 3所示.根据式（2）对不同粒级的lg（lg R0/R）与lg t的关系曲线进行线性拟合，得到不同粒级的动力学参数n值，进一步利用式（3）计算动力学参数k值，结果如表5所示.

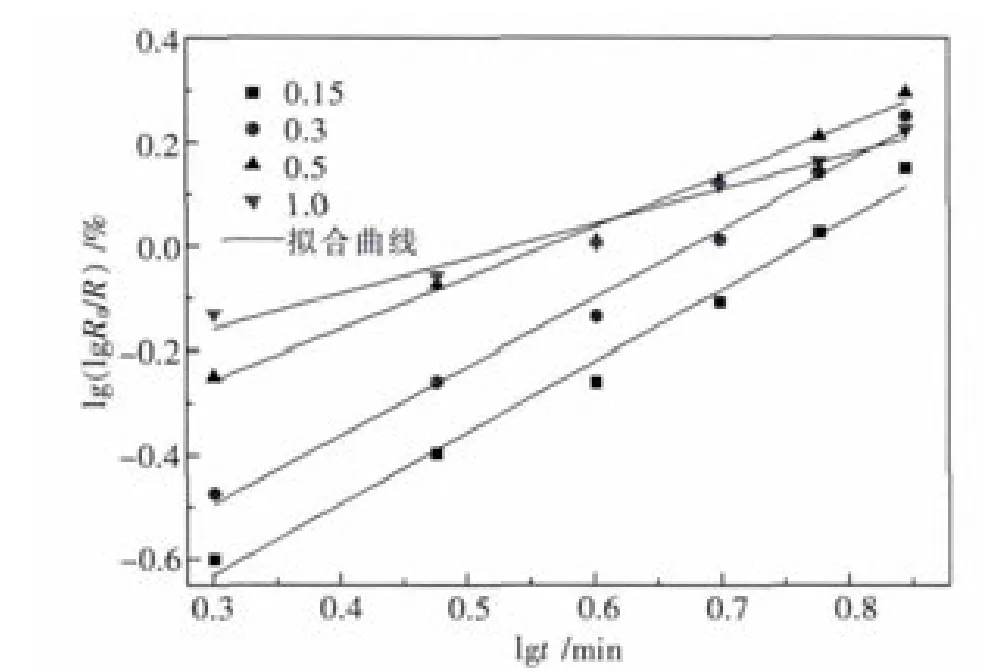
图3 不同粒级的lg（lg R0/R）与lg t的关系曲线图Fig.3 Relationship curve between the lg（lg R0/R）values of different particle sizes and lgt

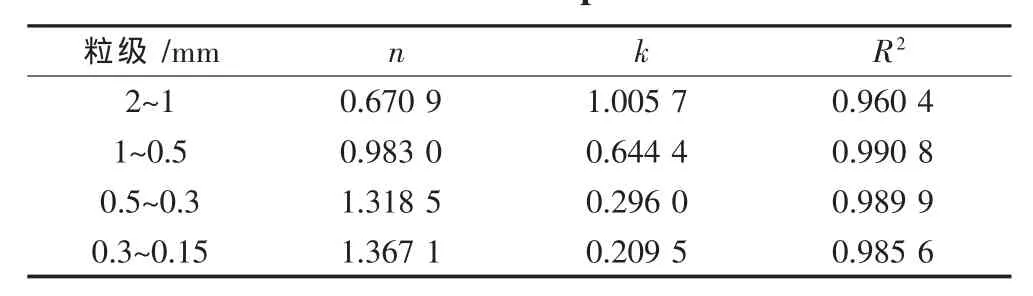
表5 不同粒级的磨矿动力学参数n和kTable 5 G rinding kinetics param eters n and k of different particle sizes

由表5可以看出，随着粒级的减小，矿粒的动力学参数n值逐渐增大，k值逐渐减小.这是因为随着矿石粒径的减少，矿粒表面裂缝相对越少，矿粒强度越高，因而表现为随着矿石粒径逐渐减小，矿石的可磨性逐渐变差直至变化不大；随着矿石粒径的减少，矿石逐渐变脆，矿石的均匀性逐渐变差[16].

3.2.2 n阶磨矿动力学方程的建立

根据表5中数据绘制动力学参数n和k与粒径d的关系曲线，并进行拟合，如图4所示.

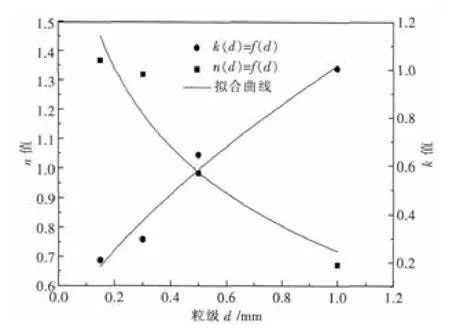
图4 动力学参数n和k与粒径d的关系曲线图Fig.4 Relationship curve between grinding kinetics param eters n and k and diam eter d

由图4可知，曲线k=f（d）呈幂函数形式，而曲线n=f（d）更接近于对数形式， 如式（9）和式（10）所示.

根据表5数据，利用Origin软件分别对式（9）和式（10）进行曲线拟合，求得未知参数 c0，c1，a0，a1和x，进而求得钨矿石的磨矿动力学参数k和n的表达式分别为：

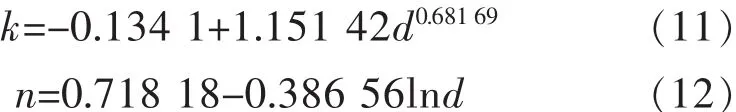
将式（11）和式（12）代入式（1）得在 0.1 mm 以上粒级的n阶磨矿动力学方程为：

3.3 磨矿动力学方程的验证

为了验证所建立的磨矿动力学方程对柿竹园钨矿石磨矿的适用性，将式（8）和式（13）建立的0.1 mm及其以下粒级与0.1 mm以上粒级的磨矿动力学方程进行计算，得到各自粒级范围内不同磨矿时间下的磨矿产品筛上累积产率理论值，结果如表6所示.

表6 不同磨矿时间下的磨矿产品筛上累积产率理论值/%Tab le 6 Theoreticalvaluesof cum ulative oversize distribution of grinding p roducts under different grinding time/%

将表6数据与表1数据进行对比，得到利用磨矿动力学方程计算的不同磨矿时间下磨矿产品不同粒级的筛上累积产率理论值与实际磨矿试验值的偏差值，结果如表7所示.

表7 筛上累积产率理论值与实际磨矿试验值的偏差值△R/%Tab le 7 Deviation values△R of theoretical values and actual grinding test values of cum u lative oversize/%

从表7可以看出，所建立的磨矿动力学方程对柿竹园钨矿石实际磨碎规律的吻合程度较高，与其它磨矿动力学模型相比，该磨矿动力学方程相对结构简单.因此，利用所建立的磨矿动力学方程为选矿厂预测磨矿产品粒度分布及进一步为通过调节磨机给矿量和分级机返砂量来控制磨矿产品粒度分布情况提供了理论依据.

4 结 论

1）对柿竹园钨矿石而言，矿粒在0.1 mm及其以下粒级符合一阶磨矿动力学，在0.1mm以上粒级则符合n阶磨矿动力学.

2）一阶磨矿动力学参数k与粒径d呈幂函数关系，其一阶磨矿动力学方程为R=R0exp[-（0.014 42+9.538 65d1.76128）t].

3）n阶磨矿动力学参数中，k与粒径d呈幂函数关系，n与粒径d呈对数函数关系，其n阶磨矿动力学方程为 R=R0exp[-（-0.134 1+1.151 42d0.68169）t0.71818-0.38656lnd].

4）所建立的磨矿动力学方程相对结构简单，而且所得到的磨矿产品筛上累积产率理论值与磨矿试验值吻合程度较高，可以用来指导选矿厂磨矿实践.

[1]马天雨，桂卫华，王雅琳，等.基于分批试验的工业球磨机粒级分布预测模型[J].北京工业大学学报， 2012，38 （9）：1281-1286.

[2]Tönshoff H K， Friemuth T， Becker J C.Process monitoring in grinding[J].CIRP Annals-Manufacturing Technology，2002，51（2）：551-571.

[3]Mizonov V E，Berthiaux H，Zhukov V P，et al.Application of multi-dimensional markov chains to model kinetics of grinding with internal classification[J].International Journal of Mineral Processing， 2004，74 （增刊 1）：307-315.

[4]刘全军，姜美光.碎矿与磨矿技术发展及现状[J].云南冶金，2012，41（5）：21-28.

[5]王志辉.建陶原料粉磨特性的试验研究[J].福建建材，2004（1）：17-19.

[6]段希祥.磨矿动力学参数与磨矿时间的关系研究[J].昆明工学院学报，1988，13（5）：23-33.

[7]侯英，丁亚卓，印万忠，等.磨矿动力学参数对磨矿速度的影响[J].东北大学学报，2013，34（5）： 708-711.

[8]李茂林，崔瑞，王非，等.阶段磨选磨矿粒度划分的理论分析与计算[J].矿冶工程，2011，31（1）：27-32.

[9]刘全军，唐荣，文书明.石英-磁铁矿体系选择性磨细研究[J].昆明工学院学报，1994，19（3）：85-89.

[10]田金星.石墨及其混合物料的磨矿动力学行为[J].中国有色金属学报，1996，6（4）：47-50.

[11]田金星，杨华，尚保平.石墨-方解石混合物料方解石组分的碎裂参数特性[J].金属矿山，2000（2）：41-43.

[12]叶贤东，文书明，张文彬.超临速磨机磨矿动力学研究[J].有色金属，2004，56（1）： 83-85.

[13]吴明珠，张成名.磨矿动力学在磨矿操作中的应用[J].有色金属，1989（5）：10-15.

[14]侯英，印万忠，丁亚卓，等.不同破碎方式下产品磨矿特性的对比研究[J].有色金属，2014（1）：5-8.

[15]印万忠，吴凯，王纪镇，等.破碎方式对紫金山铜金矿石可磨性及浮选的影响[J].福州大学学报，2014，42（2）： 321-326.

[16]王力，张常法，张军，等.助磨剂对煤沥青磨矿动力学的影响[J].山东科技大学学报，2008，27（5）：23-26.

[17]刘晓，徐超，李波.煤沥青水浆干法制备的磨矿试验研究[J].广东化工，2011，39（23）：82-84.

[18]王舒娅，龙光明，祁米，等.磨矿时间对天青石粒度和锶质量分数分布的影响[J].化工矿物与加工，2011（7）： 8-10.

[19]王敏，丁浩.搅拌磨湿法超细磨矿过程动力学的研究[J].中国非金属矿工业导刊，1999（2）：21-23.

[20]陈炳辰，周凌嘉，仲崇波.邦德功指数模拟计算方法的研究[J].金属矿山，1990（8）：36-39.

[21]仲崇波，王成功，陈炳辰.邦德棒磨功指数模拟计算方法的研究[J].中国矿山，1997，6（2）：48-52.

[22]Ahmadi R，Hashemzadehfini M，Amiri Parian M.Rapid determination of bond rod-mill work index bymodeling the grinding kinetics[J].Advanced Powder Technology，2013（24） ：441-445.

[23]Bozkurt V，Özgür I.Dry grinding kineticsof colemanite[J].Powder Technology， 2007，176：88-92.

[24]Ipek H.The effects of grinding media shape on breakage rate[J].Minerals Engineering， 2006（19）：91-93.

[25]Ian Bailon-Poujol， Jean-Paul Bailon， Gilles L’Espérance.Ballmill grinding kinetics ofmaster alloys for steel powdermetallurgy applications[J].Powder Technology， 2011，210：267-272.

[26]Heekyu Choi， Woong Lee， Seongsoo Kim.Application of grinding kinetics analysis of inorganic powders by a stirred ball mill[J].Korean Journal of Chemical Engineering， 2009，26 （6）：1806-1812.

[27]Fuerstenau DW，De A，Kapur P C.Linear and nonlinear particle breakage processes in comminution[J].International Journal of Mineral Processing， 2004，74：317-327.

[28]Teke E，Yekeler M，Ulusoy U，et al.Kinetics of dry grinding of industrialminerals：calcite and barite[J].International Journal of Mineral Processing， 2002，67（1）：29-42.

[29]段希祥.碎矿与磨矿[M].北京：冶金工业出版社，2012.

[30]陈丙辰.磨矿原理[M].北京：冶金工业出版社，1989.