改进物元可拓模型在采空区安全性评价中的应用

陈国芳， 于兆绚， 周盼

（江西理工大学资源与环境工程学院，江西 赣州 341000）

开采过程中所形成的采空区是地下金属矿山的主要灾源之一[1-2].采空区的大量存在致使井下安全状况恶化，诱发一系列灾害，如片帮冒落、地表塌陷、含水层裂隙导通等，严重的甚至造成井下人员伤亡事故.因此，对采空区安全性的合理评价，进而对采空区进行治理，以保障井下安全生产意义重大.目前，有关采空区安全性评价的研究众多.彭欣等[3]运用有限元数值模拟手段，对井下特大采空区稳定性模拟分析，取得了良好效果.罗周全等[4-5]将采空区三维实体建模与有限差分手段耦合，精确评价了某地下矿山隐患空区安全性等级.除此之外，模糊评价、未确知测度理论、可靠度理论[6-8]等方法也已应用到采空区安全性评价，并得到推广应用.然而，影响采空区安全性的因素具有不确定性和隐蔽性[9]，且各影响因素之间存在不相容性，这使得上述评价方法存在一定不足.学者蔡文所创立的可拓学理论，立足于解决多因素不相容问题[10]，恰好为采空区安全性评价问题提供了一种思路.为此，本文将从采空区安全性的影响因素入手，构建采空区安全性评价指标体系.通过物元构造、关联度求解和权重确定等步骤，构建采空区安全性评价的改进物元可拓模型，并将所建模型用于某矿山采空区安全性评价，以期获得准确合理的评价结果.

1 采空区安全性评价指标体系

影响采空区安全性的指标因素众多，参考有关研究成果[11-12]，将岩石质量、环境条件和采空区赋存状况确定为影响采空区安全性的3大类主要因素.本着指标与评价结果关联度高、全面且突出重点、易于获取等原则，进一步划分得到，岩石质量因素包括单轴抗压强度、RQD（Rock Quality Designation，岩石质量指标）值、节理间距、地下水状况和结构面特征.环境因素包括外部扰动、空区暴露时间和支护状况.空区赋存因素包括顶板暴露面积、采场埋深、采场跨度、采场跨高比和矿柱比值.据此，构建采空区安全性评价指标体系见表1.

2 采空区安全性物元可拓评价模型

给定对象N，它关于特征C的量值为V，以有序三元组R=（N，C，V）作为描述对象的基本元，简称物元.物元评价方法是以可拓集合论为数学基础[13]，运用关联函数表达元素和集合的可变属性，通过物元变化与可拓子集域计算，求得给定对象的相容度，用于判断或评价的方法.

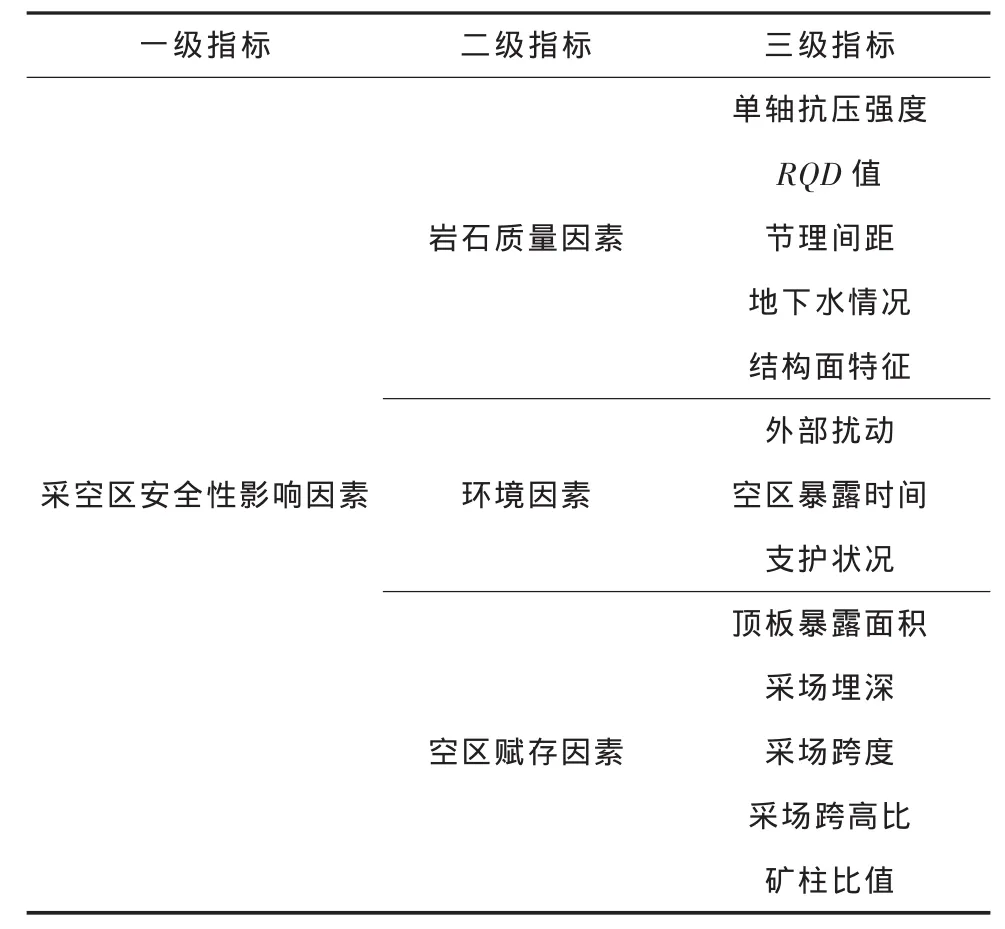
表1 采空区安全性评价指标体系Table 1 System of safety evaluation indeses on goaf

2.1 物元构造

将采空区安全性划分为t个等级，评价指标ci（i=1，2，…，n）对应 t等级的取值区间为[ati，bti]，则经典域物元 Rt与节域物元 Rs分别为式（1）和式（2）：

式（2）中，[asi，bsi]为评价指标 ci对应所有安全性等级的取值区间.

对于待评价空区 Nj（j=1，2，…，m），获取其评价指标ci的量值，得到待评价物元Rj，如式（3）所示.

2.2 关联度求解

待评价物元Rj在t等级时，对应于指标ci的关联度 ktj（vti）为：

式（4）、式（5）中，vji为 Rj对应指标 ci的量值，vti为 ci的经典域范围[ati，bti]，vsi为节域范围[asi，bsi]，y0对应于vji，y 对应于 vti和 vsi.

2.3 采空区安全性评价

对评价指标ci赋以权重Wi，则待评价物元Rj对应安全性等级 t的综合关联度 ktj（Nj）为

最大综合关联度所对应的等级t即为待评价采空区的安全性等级.

3 物元可拓评价模型的改进

3.1 物元量值归一化

采用物元可拓评价模型时，若待评价物元的量值超出节域范围，关联函数便会失效，导致关联度无法求解.为此，这里通过隶属函数[14]对物元量值归一化，同时解决了因评价指标量纲不同而存在的不可度性，操作方法如下.

1）对效益型指标（值越大越好）：

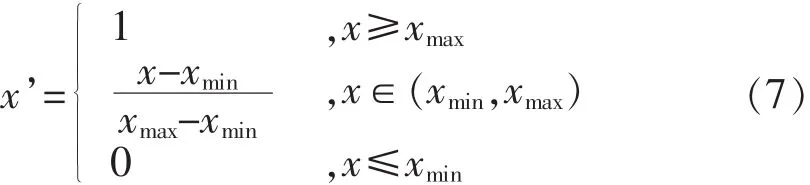
2）对成本型指标（值越小越好）：

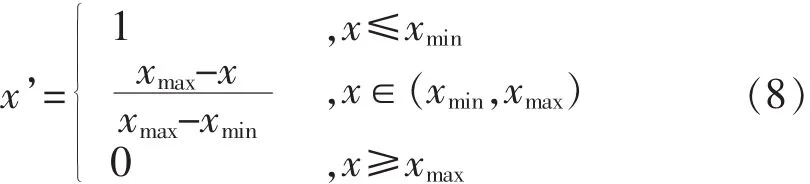
式（7）、式（8）中，x 与 x’对应归一化前后的物元量值，xmax与xmin为评价指标区间中的最大和最小量值.

3.2 评价指标权重修正

物元可拓方法中，权重计算效率低，易陷入循环[15].为此，采用改进层次分析法修正权重，具体思路是在权重求解过程中，定义诱导矩阵 C=（1）m×n，通过分析判断矩阵与诱导矩阵的关系，以对判断矩阵的一致性进行改进.算法原理参见图1.

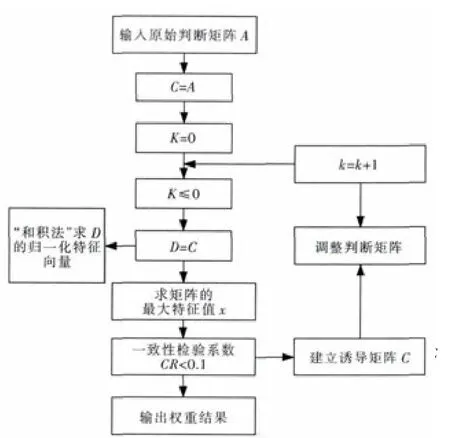
图1 改进层次分析法原理Fig.1 Theory ofmodified AHPm ethod

4 工程应用

4.1 评价指标分级

北方某金矿直属矿区属滨海开采，矿区构造活动不甚强烈，区内浅层的第四系松散层较厚，基岩岩性为较坚固变质岩和岩浆岩.依据采空区安全性分级研究[16]，将采空区安全性划分为5个等级，依次是：I级（非常稳定）、II级（稳定）、III（中等稳定）、IV 级（不稳定）、V级（非常不稳定）.结合该矿山生产实际条件，确定其采空区安全性评价指标分级标准（表2）.

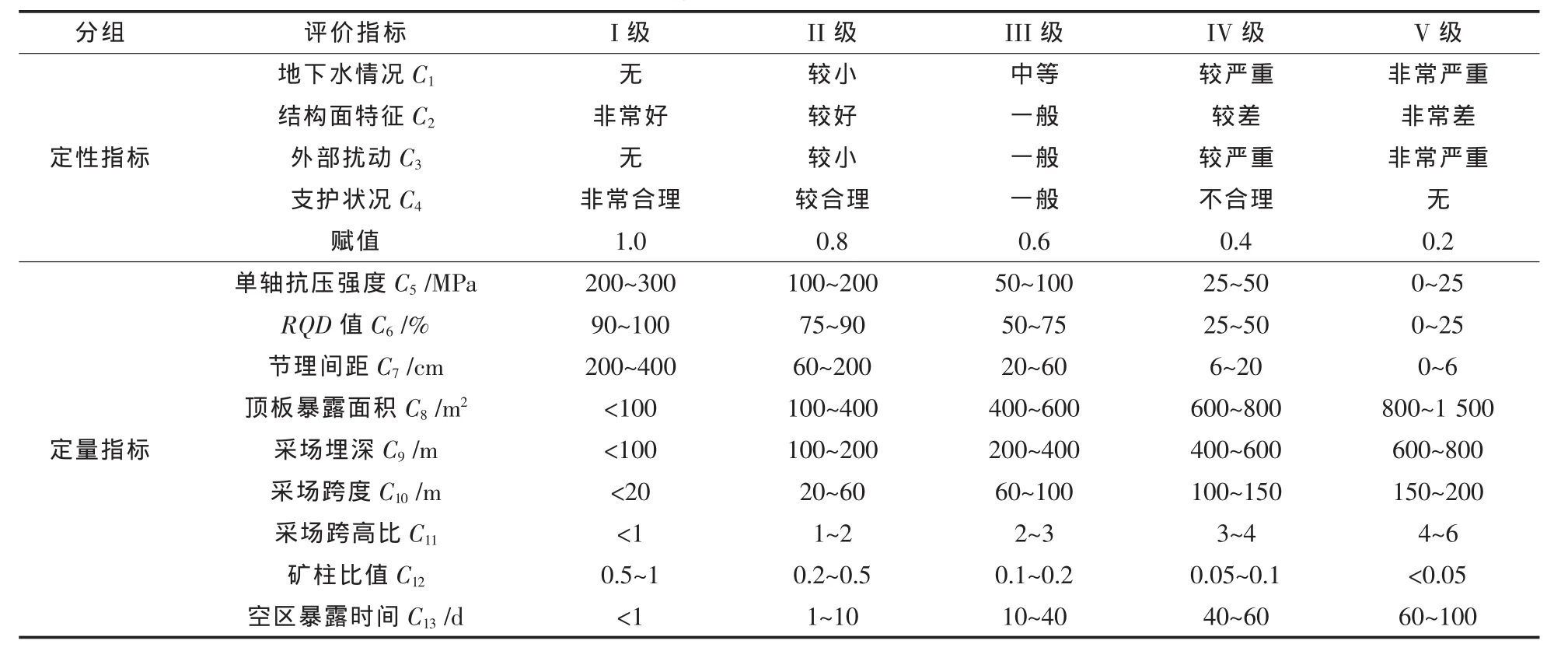
表2 评价指标分级标准Table 2 G rading standard of evaluation indexes

4.2 物元构造

根据物元构造方法（式（1）～式（3）），对应采空区安全性分级（表 1），通过隶属函数（式（7）和式（8））对物元量值归一化，构造经典域物元Rt，如式（9）所示；

以及节域物元Rs，如式（10）所示.

以矿山-510 m中段S511等6个采空区为评价对象，其单项评价指标取值参见表3.

根据隶属函数公式，对表3中指标取值归一化处理，构造待评价物元Rj，如式（11）所示.

4.3 评价结果

按图1中改进层次分析法流程，计算评价指标权重矩阵 Wi= （0.05， 0.091 7， 0.056， 0.027 8，0.075， 0.05， 0.066 6， 0.112 5， 0.112 5， 0.087 5，0.087 5， 0.1， 0.027 8）.根据式（5），计算待评价物元Rj对应各安全性等级的关联度，进而获得采空区安全性评价结果 （表4）：S511和 N511n空区为 II级（稳定），N511s、513 和 516 空区为 III级（中等稳定），512空区为IV级（不稳定）.为验证评价结果的准确性，将其与模糊评价模型比较（表 4）.不难看出，除512空区外，2种模型的评价结果完全一致.

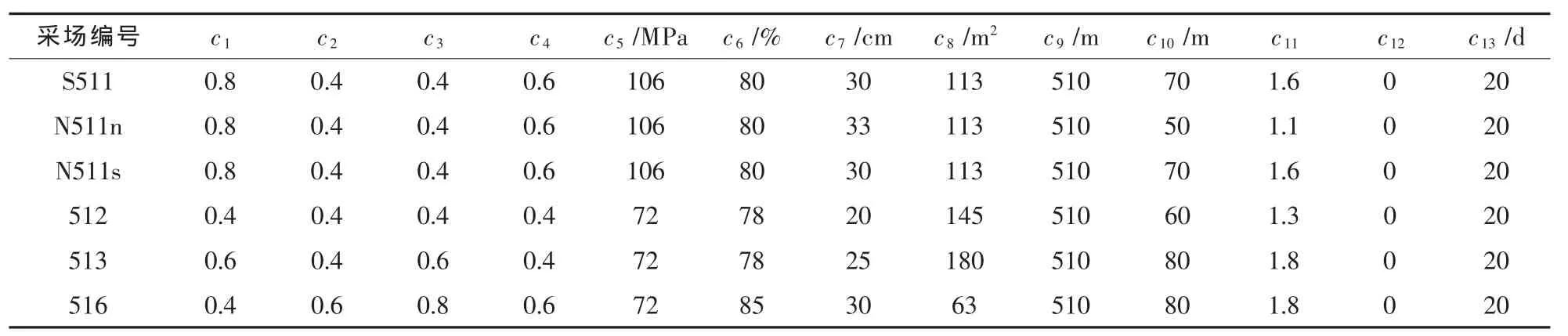
表3 待评价采空区对应指标取值Table 3 Values of opposite indexes of goaf being evaluated

表4 评价结果对比Table 4 Com parison of evaluated results

4.4 分析验证

对于512空区，采用改进物元可拓模型和模糊评价模型得到的评级结果分别为IV级（不稳定），III级（中等稳定）.采用空区探测系统对512空区进行探测，将探测数据导入实体建模软件，获得该空区三维实体模型（图 2（a）），进而导入 FLAC3D有限差分软件，生成空区数值分析模型（图 2（b））.

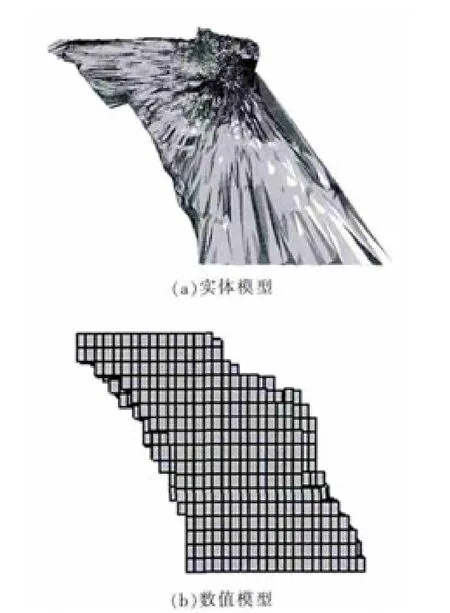
图2 空区模型F ig.2 Cavity model

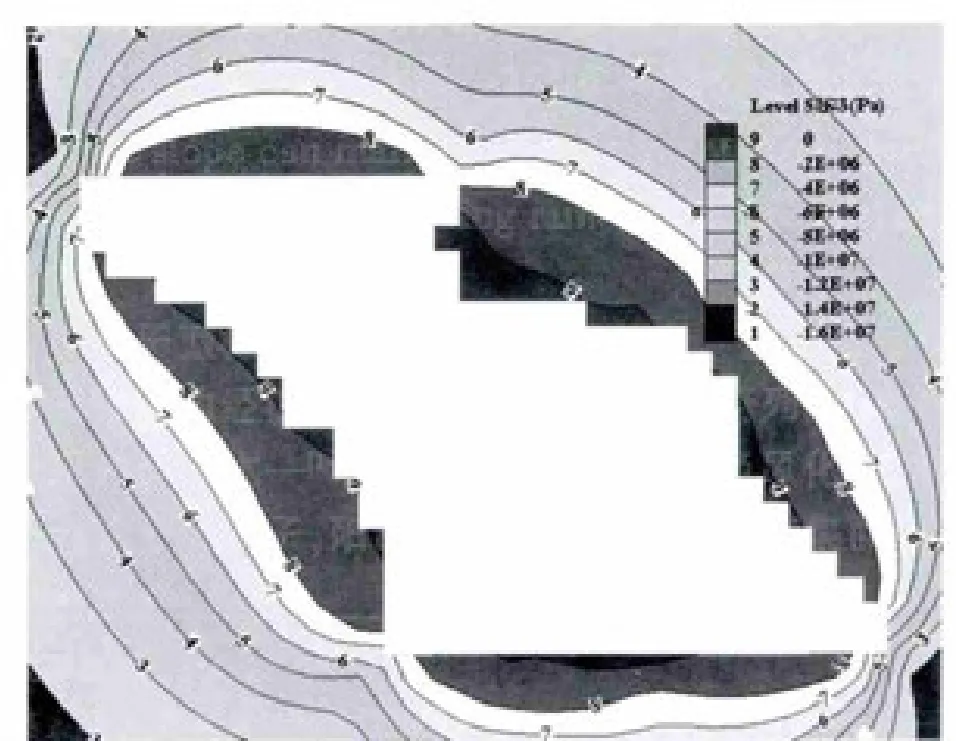
图3 最小主应力分布F ig.3 Distribution ofm inim um p rincipal stress

图4 塑性区分布F ig.4 Distribution of p lastic zone

根据圣维南原理，计算模型尺寸定为：150 m×150 m×100 m（长×宽×高）.计算采用摩尔库伦本构模型[17]，通过快速应力边界法生成初始地应力场.按实际情况进行空区开挖数值模拟，得到空区应力分布特征及塑性破坏情况见图3和图4.由图3可知，空区最大拉应力值达到1.7 MPa，超过围岩抗拉强度，形成了一定范围的拉应力区（FLAC3D中定义拉应力为正，压应力为负）.图4则反映了空区周边形成一定规模的塑性破坏区.结合现场实测及数值分析结果，确定该空区内已产生了一定规模的失稳破坏，且存在进一步破坏的可能.因此，将512空区的安全性等级定为IV级（不稳定）较III级（中等稳定）更为准确.

5 结 论

1）从岩石质量、环境条件和采空区赋存情况3大类因素出发，细化分析，选取单轴抗压强度等13类指标，构建采空区安全性评价指标体系.基于物元可拓理论，通过隶属函数归一化物元量值，采用改进层次分析法计算指标权重，建立了采空区安全性评价的改进物元可拓模型.将该模型用于某金矿采空区评价实例，评价结果为：II级（稳定）空区2个，III级（中等稳定）空区3个，IV级（不稳定）空区1个.

2）将改进物元可拓模型与模糊模型的评价结果进行对比，仅有1个采空区的评价结果不符.对该空区进行现场探测，并采用数值手段分析其安全性，结果表明，该采空区已产生一定规模的失稳破坏，且存在进一步破坏的可能.因此，改进物元可拓模型的评价结果（IV级，不稳定）更符合实际情况，将其用于采空区安全性评价是合理可靠的.

[1]李夕兵，李地元，赵国彦，等.金属矿地下采空区探测、处理与安全评判[J].采矿与安全工程学报，2006，23（1）：24-29.

[2]罗明生，王浩文，李本尧，等.铜矿北部47-49线特大采空区治理研究与实践[J].江西理工大学学报，2008，29（5）：12-14.

[3]彭欣，崔栋梁，李夕兵，等.特大采空区近区开采的稳定性分析[J].中国矿业，2007，16（4）：70-73.

[4]罗周全，刘晓明，吴亚斌，等.基于Surpac和Phase2耦合的采空区稳定性模拟分析[J].辽宁工程技术大学学报（自然科学版），2008，27（4）： 485-488.

[5]杨彪，罗周全，刘晓明，等.基于有限元分析的复杂采空区群危险度分级[J].矿业工程研究，2010，25（1）：4-8.

[6]罗周全，张旭芳，刘晓明，等.基于模糊模式识别的金属矿采空区危险性综合评价[J].安全与环境学报，2010， 10（3）： 195-199.

[7]Dong L J， Peng G J， FU Y H， et al.Unascertained measurement classifying model of goaf collapse prediction[J].Journal of Coal Science and Engineering， 2008， 12（2）： 221-224.

[8]赵奎，蔡美峰，饶运章，等.采空区块体稳定性的模糊随机可靠性研究[J].岩土力学，2003，24（6）：987-990.

[9]王新民，柯愈贤，鄢德波，等.基于熵权法和物元分析的采空区危险性评价研究[J].中国安全科学学报，2012，22（6）：71-77.

[10]杨春燕，蔡文.可拓工程[M].北京：科学出版社，2007.

[11]汪伟，罗周全，王益伟，等.金属矿山采空区危险性辨识的遗传BP模型研究[J].中国安全科学学报，2013，23（2）：39-44.

[12]杜坤，李夕兵，刘科伟，等.采空区危险性评价的综合方法及工程应用[J].中南大学学报（自然科学版）， 2011， 42（9）： 2802-2811.

[13]康志强，冯夏庭，周辉.基于层次分析法的可拓学理论在地下洞室岩体质量评价中的应用[J].岩石力学与工程学报，2006，25（增刊）： 3687-3693.

[14]张慧颖，曾建民.物元可拓模型的改进及其在膨胀土分类中的应用[J].岩土力学，2008，29（6）：1681-1684.

[15]李梅霞.AHP中判断矩阵一致性改进的一种新方法[J].系统工程理论与实践， 2000，20（2）： 122-125.

[16]罗一忠.大面积采空区失稳的重大危险源辨识[D].长沙：中南大学，2005.

[17]张友锋，袁海平.FLAC3D在地震边坡稳定性分析中的应用[J].江西理工大学学报，2008，29（5）：23-26.