一种基于遗传算法的神经网络结构优化方法

付 琦

（山东农业工程学院，济南 250100）

一种基于遗传算法的神经网络结构优化方法

付 琦

（山东农业工程学院，济南 250100）

0 引言

近年来，人工神经网络（ANN）提供了一种新的方法来模拟复杂而又难以定义的问题，ANN已经在智能控制、机器人、模式识别、计算机视觉、生产过程优化和信息处理等多种领域中取得了广泛应用[1～4]。研究结果表明，如果ANN的网络结构太大，将导致归纳性较差，反之，太小的网络结构则会造成学习能力偏低。因此，如何能够快速而准确地设计ANN网络结构一直以来都是工程领域和研究领域备受关注的热点问题[5]。ANN网络结构优化问题就是要确定ANN网络中隐藏层的最优数量，每一层中的神经元数量及合适的激活函数，以便尽量提高人工神经网络的性能[6]。

ANN网络结构优化方法有很多种，文献[7]利用主成分分析法确定输入层结点数，可使问题得到一定的解决，但是当样本数据很大时，样本集本身没有包含全部样本的特征，将导致预测的结果出现较大的误差。文献[8]利用模糊聚类法首先对样本进行分类，然后再从每一类中按一定比例选择学习样本，但在分类时，究竟应将样本数据分为几类往往随意性很大。文献[9]针对小波神经网络提出了一种基于自适应投影算法的结构优化方法，但该方法计算量较大，处理过程相对较复杂。文献[10]针对神经网络的结构存在冗余的问题, 提出了一种利用粗糙集优化神经网络结构的方法，该方法以粗糙集数据分析为基础，缺乏对决策原理的渗入阐述。

本文提出了一个新的基于数学规划的ANN网络结构优化方法，应用遗传算法找到最佳的隐藏层、激活函数和矩阵的权重，并将这个问题作为一个具有非混合约束的线性规划，最终通过遗传算法来解决。这样设计之后，可以调整用于学习或者训练的ANN结构权重矩阵，得到最佳的网络结构。本文的组织如下：第2节介绍了人工神经网络，第3节提出了神经优化问题的架构和建模思路，第4节展示了如何通过遗传算法来解决这个问题，第5节进行试验验证，第6节总结全文。

1 神经网络结构

1.1 多层网络结构

1969年，研究人员M. Minsky和S. Papert首次提出多层神经网络（MLN）的概念[11]。MLN网络在输入和输出层间有一或多个隐藏层，其结构如图1所示，同一层中神经元间没有链路。一般来说，每个神经元与下一层中的所有神经元相连。

如图1所示，本质上来说，人工神经网络属于暗箱运算，利用一组非线性基函数将输出与输出联系起来。ANN网络的基本单元是神经元，包括简单的同步处理元素，由生物神经系统激活。利用一组输入数据及实际测量值得出的相应输出数据（输入/输出对）来训练ANN网络，以便使一组输入尽可能准确地得出一组目标输出。许多研究已经证明，MLN网络可有效求解多种复杂问题。

1.2 神经网络训练

在训练ANN网络时需要调整神经元间每条链路的权重，直到每组输入数据计算出来的输出与实验数据输出尽可能地接近。连续层中的神经元互相连接，每个神经元计算其输入的权重之和，而输出需要计算该值经过激活函数调整过的值。比如，该激活函数可为S形函数：

训练过后，网络不仅可以对学习基点再生理想的输出，对其他输入也可以再生理想输出，这个过程称为泛化。

1.3 输入层

1.4 隐藏层

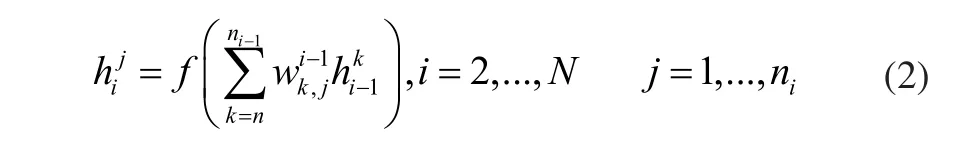
1.5 输出层

输出层中的神经元可收集hN隐藏层的输出，输出层的神经元计算如下：

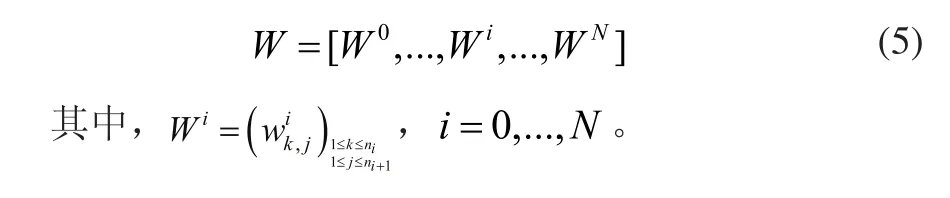
2 神经网络结构优化建模

为了对神经架构优化问题建模，神经网络的输出可计算如下：

其中，U=[u1,…,ui,…,uN-1]，其中向量ui的取值为0或1。

如图2(a)所示，首个隐藏层的输出可计算如下：

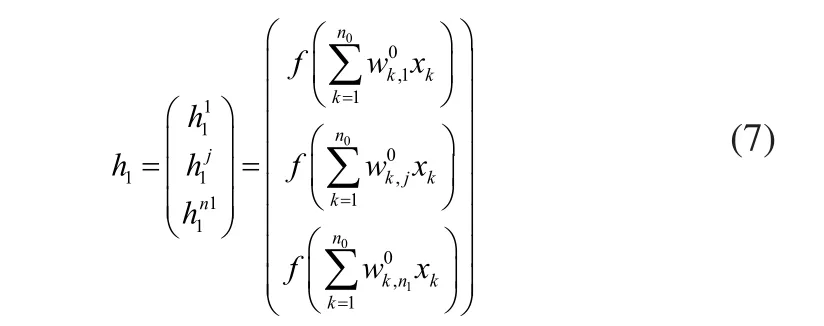
隐藏层i计算出来的输出：

如图2(b)所示，最后一个隐藏层计算如下：

如图2(c)所示，神经网络的输出计算如下：

优化目标函数：数学规划模型的目标函数表示计算输出和预期输出间的误差：

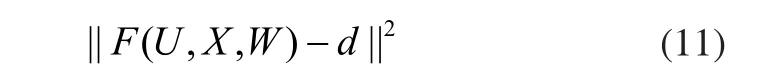
最后约束可保证存在隐藏层：

在本文中，我们的优化目标是调整ANN网络结构的权重矩阵，我们将上述问题表述为一种固定变量非线性规划问题下，并通过遗传算法对其进行解决。

3 遗传算法求解非线性规划模型

遗传算法（Genetic Algorithm，GA）属于“进化算法”概率方法，已经在通信、路由、调度等多种领域的优化问题中得到应用[12]。GA算法以选择和变异规则为基础。每一个解表示一个或多个染色体被编码的一个个体，这些染色体表示问题中的变量。首先，生成由固定数量个体组成的初始种群，对选择出来的一组个体进行繁殖操作，交换其适应度。这一步骤一直持续至到达最大数量迭代次数为止，具体步骤如下：

1）初始种群

图2 神经网络各层之间的计算方法

随机产生N个初始串结构数据，每个串结构数据称为一个个体。N个个体，构成了一个群体，这个参数N需要根据问题的规模而确定。初始种群中的个体随机生成，其中向量“u”的变量取值0或1，权重矩阵从IR空间中随机取值。

2）个体评估

计算交换产生的新个体的适应度，适应度用来度量种群中个体优劣（符合条件的程度）的指标值，这里的适应度就是特征组合的判据的值。这个判据的选取是GA的关键所在。在该步骤中，根据个体表现为各个个体相应分配一个称为适应度的数值；从本质上来讲，它取决于该个体的目标函数值。个体的适应度越大，匹配度越高。本文中的适应度如下：

其中，M是一个远大于零数值，使“objective”目标函数值最小，等价于使适应度函数的值最大。

3）选择

选择的目的是为了从交换后的群体中选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。采用RWS（Roulette Wheel Selection）轮盘方法作为本文的选择方法；该方法是一种比例型选择方法，根据个体的适应度来选择个体，这一步骤的存在使得当前群体是所有搜索过的解之中是最优的前N个的集合。

4）变异

变异是算法中非常重要的一个步骤。该步骤中，根据种群中选择出来的个体（父母）来生成新的个体（子嗣）。子个体构建方法如下：我们固定一个变异点，母个体在该点切开，母个体1的第1部分与母个体2的第2部分属于子个体1，其他部分属于子个体2。在我们采用的变异策略中选择不同的变异点，第1个变异点指向权重矩阵，第2个针对向量U。

4 试验结果验证

我们在本小节将通过一些数值示例来阐述本文方法的验证，本文采用多层网络架构，该架构使用的激活函数为：

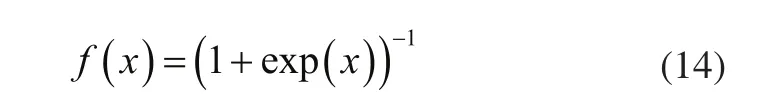
这里，我们采用均方根误差（RMSE）来评估统计性能，计算方法如下：

其中，Yi表示实际数值（计算出来的），d表示预测数值，其中第ith个观测值从1～Q计数，Q表示总观测值的数量。

试验结果如表2所示，可以看出，针对不同的ANN，通过本文的算法优化均可以给出最佳的网络结构优化策略，优化后的最佳隐藏层数量比设计值降低了30%左右，平均RMSE指标小于1，从中可以看出本文中理论结果及新模型的有效性。

表1 神经网络结构优化试验结果

5 结论

本文针对神经网络架构优化问题提出了一种基于遗传算法的结构优化方法，尤其适合于求解复杂的非线性问题。经测试，该方法可确定ANN网络中隐藏层的最优数量及最优权重矩阵，以便使预期（预测）输出与计算输出间的误差最小。这些参数的确定对ANN网络的性能具有一定影响。此外，本文方法从本质上来讲非常容易实现并行化。

[1]梁捷,陈力.执行器受限空间机器人的模糊神经网络控制[J].工程力学.2014,(11):190-197.

[2]李震宇.基于神经网络的计算机网络安全评价研究[J].电子制作.2014,(19):118.

[3]黄芳,吴小良.基于BP神经网络的转炉出钢过程氧含量预测及优化[J].热加工工艺.2013,(01):48-50.

[4]龚静,陈向东,时子青.基于CS和神经网络的传感器网络模式识别研究[J].传感器与微系统.2011,(12):62-64.

[5]杨钟瑾,史忠科.神经网络结构优化方法[J].计算机工程与应用.2004,(25):52-54.

[6]Wang D.Fast Constructive-Covering Algorithm for neural networks and its implement in classification[J].Applied Soft Computing.2008,8 (1):166-173.

[7]陈小前,罗世彬,王振国,等.BP神经网络应用中的前后处理过程研究[J].系统工程理论与实践.2002,(01):65-70.

[8]何勇,项利国.基于模糊聚类的BP神经网络模型研究及应用[J].系统工程理论与实践.2004,(02):79-82.

[9]潘玉民,张晓宇,张全柱,等.基于量子粒子群优化的小波神经网络预测模型[J].信息与控制.2012,(06):741-746.

[10]夏红霞,王惠营,胡磊.基于粗糙集的神经网络结构优化方法[J].计算机与数字工程.2010,(05):49-51.

[11]Cichoki A, Unberhuen R.Neural Network for Optimization and signal processing.

[12]李敏远,都延丽.基于遗传算法学习的复合神经网络自适应温度控制系统[J].控制理论与应用.2004,(02):242-246.

A novel method for neural network structure optimization based on genetic algorithm

FU Qi

神经网络隐藏层数量的选择以及权重值的确定对训练算法的收敛性有很大影响，为了解决神经网络（ANN）训练过程中结构复杂的问题，提出了一种基于遗传算法（GA）的网络结构优化方法。试验结果表明，在训练样板数量较大时，优化后的ANN能够计算出隐藏层的最佳数量，从而提高整体的性能，具有较好的泛华能力。

神经网络；结构优化；遗传算法；非线性优化

付琦（1982 -），男，山东济南人，讲师，硕士，研究方向为计算机科学与技术。

book=74,ebook=406

TP18

A

1009-0134(2015)07(下)-0071-04

10.3969/j.issn.1009-0134.2015.07(下).22

2015-03-18