中国房地产价格指数期货的设计与定价研究

■ 胡岳峰，席 爽，吴鑫育，周海林

一、引言

房地产行业是一个高成本、高收益以及高风险的“三高”行业。近年来，伴随着中国房地产行业飞速发展，也产生了高价格、高房屋闲置率以及高不良贷款率的“三高”问题。针对这问题，从2009年12月以来国务院对楼市进行一系列的政策调控，2010年出台 “国十一条”、“国十条” 以及 “9·29新政”，2011年出台“新国八条”，2013年出台“国五条”；中国人民银行也多次对住房公积金存贷款利率进行调节，旨在进行限购、限贷，打击投机购房，但是各大城市的房价依然具有上升趋势，使得中国房地产市场呈现出“非理性繁荣”的局面。在行政手段干预市场无力的情况下，市场经济手段对经济问题的解决具有必要性。期货作为重要的金融衍生品之一，具有发现价格、管理风险、套期保值等功能，而房地产价格指数期货可以有针对性地解决房地产市场的问题，打破房地产单边交易市场的局面，建立多空双边交易机制，使房地产市场价格回归理性，为投资者规避风险提供有效渠道，也为政府部门对楼市调控以及宏观经济政策制定提供参考。

国外关于房地产金融衍生品的研究较早，理论发展较为成熟，主要从房地产金融衍生品市的构建及其意义和定价模型的提出及完善两方面展开。

在房地产金融衍生品市的构建及其意义方面，Shiller等（1993)首次提出建立房地产价格指数期货与期权市场，认为房地产金融衍生品市场相对于其他金融衍生品市场具有交易门槛低的优势，并且能为房地产投资者扩展投资渠道，分散投资风险。Shiller等(1996)分析了房地产价格和抵押贷款违约风险的关系，认为房地产价格指数期货与期权市场的建立可以使得套期保值在房地产按揭贷款投资组合上的运用，从而能够降低抵押贷款违约风险。Fisher(2005)提出发展基于美国不动产协会商用不动产指数的新型互换，这种互换相对于产权式互换在调整投资组合与规避房地产市场风险方面更具优势。

在房地产金融衍生品定价模型的提出及完善方面，Buttimer等(1997)提出以房地产价格指数和即期利率的双变量房地产衍生品定价模型，该模型利用房地产价格指数计算出房地产市场的波动率来对房地产金融衍生品进行定价，并对美国商业房地产价格指数互换进行实证分析。Bjork和Clapham(2002)对Buttimer等(1997)提出的定价模型进行了完整的数学证明，讨论了原模型中参数估计值的误差。Otaka和Kawaguchi(2002)提出了基于三个独立市场的定价模型，即证券市场，租赁市场和房地产市场，考虑市场的不完善性，采用风险最小化策略为房地产市场证券进行定价。Geltner和Fisher（2007)考虑房地产价格指数的滞后性对定价的影响，运用市场均衡理论为房地产远期和互换合约定价。Patel和Pereira(2008)考虑了交易对手违约风险，在相同的假设条件下扩展了 Bjork和Clapham(2002)对房地产指数总报酬交换的定价模型，并利用英国商业地产指数进行实证分析。Baran等(2008)运用极大似然估计法和卡尔曼滤波将Schwartz和Smith(2000)提出的两因素商品定价模型应用于房地产衍生品市场。Ciurlia和Gheno(2009)考虑到房地产市场对利率期限结构的敏感度，使用包含房地产资产价值和即期利率波动的两因素模型为欧式期权和美式期权定价，但是并未得到封闭的解析解。Cao和Wei(2010)在均衡估值框架对房地产指数衍生品价格进行研究,得到封闭形式的估值方程。Fabozzi等(2012)运用均值回归过程来对房地产金融衍生品包括期货、期权、远期和总报酬互换定价，从而形成一个房地产金融衍生品定价模型框架,并运用鞅估计方法对模型中的参数进行估计。

国内在房地产价格指数期货的研究还不够深入，大多数也只是停留在房地产价格指数期货推出的可行性、必要性以及政策性建议等定性问题的探讨，对房地产价格指数期货的设计并未给出完整且系统的方案；关于房指金融衍生品定价等定量问题的研究更是屈指可数，周佰成(2013)、王建飞（2013)、庞丽艳等（2013）采用 Fabozzi等（2012）提出的定价模型进行实证分析，但对模型中的参数估计并未给出明确的方法。

综上所述，本文兼顾中国房地产价格指数期货研究的定性与定量两个层面，首先借鉴目前世界各地已经推出的房地产价格指数期货合约与中国股票指数期货合约的经验，并结合笔者提出的“推出中国首只迷你型或中小型指数期货”的设计思想设计出中国房地产价格指数期货合约，并在此基础上利用Fabozzi等（2012）提出的房地产金融衍生品定价模型对设计的期货合约进行定价。进一步，运用极大似然（ML）估计方法对模型参数进行估计。最后，选取中国房地产指数系统 （China Real Estate Index system,CREIS）下的北京、上海、广州、深圳等地的新房价格指数中的城市综合指数进行实证分析，为未来中国房地产价格指数期货的推出提供理论支持。

二、中国房地产价格指数期货合约的设计

目前，在世界范围内推出房地产价格指数期货主要有：2006年5月芝加哥商品交易所(Chicago Mercantile Exchange，CME)推出的以标准普尔凯斯—希勒房价 （S&p/Case-shiller Home Price Index，CSI）为标的的房地产价格指数期货，期货合约的数据来源于美国波士顿、芝加哥、丹佛、拉斯维加斯、洛杉矶、迈阿密、纽约、圣地亚哥、旧金山和华盛顿十个城市的加权综合指数；2009年9月欧洲期货交易所 (Eurex)推出的以英国IPD年度财产指数(IPD UK Annual Property Index)为标的的房地产价格指数期货；2012年2月芝加哥期权期货交易所(CBOE Futures Exchange,CFE)推出的以包括25个市区的RPX综合指数期货(RPXCP)。由于数据及资料有限，笔者根据以上房价指数期货合约的一至两种及中国沪深300股指期货合约来设计中房指数期货合约。

（一）设计思想

在经济全球化背景下，各个国家与地区都面临着前所未有的市场竞争,进行金融产品的创新成为各国金融市场进行竞争的共识，降低市场参与门槛是吸引更多的交易者尤其是中小投资者的重要途径。其中,迷你型或中小型指数期货交易备受各国的关注和推崇。迷你型或中小型指数期货合约价值较小,交易成本较低,这些优势使其广受中小投资者欢迎。纵观中国股指期货市场，投资群体多局限于投资基金、各大券商与上市公司等大型机构投资者。随着中国金融市场的发展，中小型与迷你型指数期货的推出是必然趋势，所以笔者所设计的中房指数期货相当于迷你型股指期货的规模，为更多的个人投资者在指数期货市场提供投资渠道，也为未来中国在国际金融市场中竞争带来优势。

（二）标的指数

目前国内各种房地产价格指数中较权威的是由中国指数研究院发布的中国房地产价格系统下的各类指数，包括百城指数、新房价格指数以及主城区二手住宅和租赁价格指数，新房价格指数下又包括住宅指数、写字楼指数、商铺指数以及结合三者价格按照一定权重编制的城市综合指数。百城指数是根据全国100个重点城市新房价格进行编制的系统性综合指数，选取该指数作为标的指数将不利于对期货种类的扩展以及单个城市期货价格的横向对比，而主城区二手住宅和租赁价格指数仅限于二手住宅价格，房地产种类不够全面，不具有代表性，与新房价格指数相比对价格的反映的时效性较低，所以本文选取新房价格指数下的城市综合指数，具有较高的代表性与时效性。

（三）合约乘数

合约乘数是期货合约价值的重要基准依据，标的指数的指数点与合约乘数的乘积得到的就是期货合约的价值，以中国沪深300股指期货为例，其合约乘数为￥300每点，2015年6月12日沪深300点数为5335.11点，那么一份合约的价值就是￥300*5335.11=￥1600533。期货合约的合约乘数决定了期货市场资金的准入门槛高低与流动性的大小，合约乘数较小可以降低资金准入门槛，使更多的投资者进入市场，带动市场的流动性，但可能导致市场波动加大、过度投机等问题，反之，又会导致交易门槛升高，市场流动性不足等问题。

根据全球主要房指期货与迷你型股指期货合约乘数，并结合2015年5月的最新相关指数数据，推算出目前全球主要房指期货与迷你型股指期货的合约价值（表1），其合约价值远远小于美国和欧洲地区的股指期货，从中可以看出西方国家的房指期货与其迷你型股指期货的合约规模是大体相当的，这也印证了笔者对中国房指期货设计思想的正确性。在中国国内已经上市的沪深300、上证50、中证500股指期货，其合约价值都在100～200万之间（表2），按照最低交易保证金比例8%计算，最低保证金基本都达到10万以上，资金门槛过高，导致中小投资者被拒之于股指期货的门外。根据2015年5月的新房指数中的城市综合指数的平均数2256点，合约乘数设为￥100每点，合约价值即为￥225600，按照最低交易保证金比例约10%计算，最低保证金达到￥22560，资金门槛适中，能为中小投资者提供投资机会，达到扩大中国期指市场投资者的参与性的目的，符合笔者设计思想。

表1 全球主要房指期货与迷你型股指期货合约乘数及合约价值（2015年5月数据）

表2 中国股指期货合约乘数及合约价值（2015年6月12日数据）

（四）最小变动价位

最小变动价位是指数期货公开竞价过程中每次报价的最小单位，它可以影响投资者的交易成本及市场的流动性与活跃程度。由于美国与欧洲地区房地产价格指数编制方法及其目前的指数额与中房指数相差较大，所以不能进行有效地类比。根据国际经验，最小变动价位占指数的万分之一较为合理，根据2015年5月的新房指数中的城市综合指数的平均点数2256点，其万分之一为0.2256点，所以在0.2256点左右都较为合理，为了便于结算，将最小变动价位定为0.2点。

（五）每日涨跌幅度

每日涨跌幅度就是每日价格的最大波动限制，涨跌幅度太大会增加市场价格的波动性，增加市场交易的风险，涨跌幅度太小会破坏市场本身的规律性，切断交易的连续性。根据中国沪深300指数期货合约的经验，在房指期货推出的初始阶段可以将涨跌幅度设置在±10%，但随着中国房指期货市场的发展与扩大，在其成熟阶段，可以适当降低涨跌幅度以维持市场稳定。

（六）最低保证金比例

最低保证金比例是买卖期货合约时按照合约价值的一定比例所要缴纳的最低金额。最低保证金的设立在于防止违约风险的发生，也可以反映该期货的杠杆效应。最低保证金比例越低，杠杆效应越大，市场投资者交易的积极性越高，但同时也会增大投资者的盈亏幅度，扩大了市场风险。根据笔者设计中国房指期货的初衷，即扩大指数期货市场参与性，以最低保证金￥10万为资金门槛，将最低保证金比例设置为10%，根据合约价值为￥225600，乘以10%，最低保证金为￥22560，加上预留的结算准备金以应付房价指数向不利方向变动追加保证金的需要，小于￥10万，在中小投资者的资金承受范围内，较为合理。

（七）合约月份及其他

根据中国房地产指数每月发布的特点，合约月份以季度为标准较为合理，标普凯斯－席勒房指期货的合约月份为2月、5月、8月、11月,考虑到中国传统，将中国房指期货的合约月份定为3月、6月、9月、12月。交易时间、最后交易日、最后交易日交易时间、交割日期、交割方式及交易场所均与沪深300股指期货相同。

根据以上条款分析，设计的中国房地产价格指数期货合约如下：

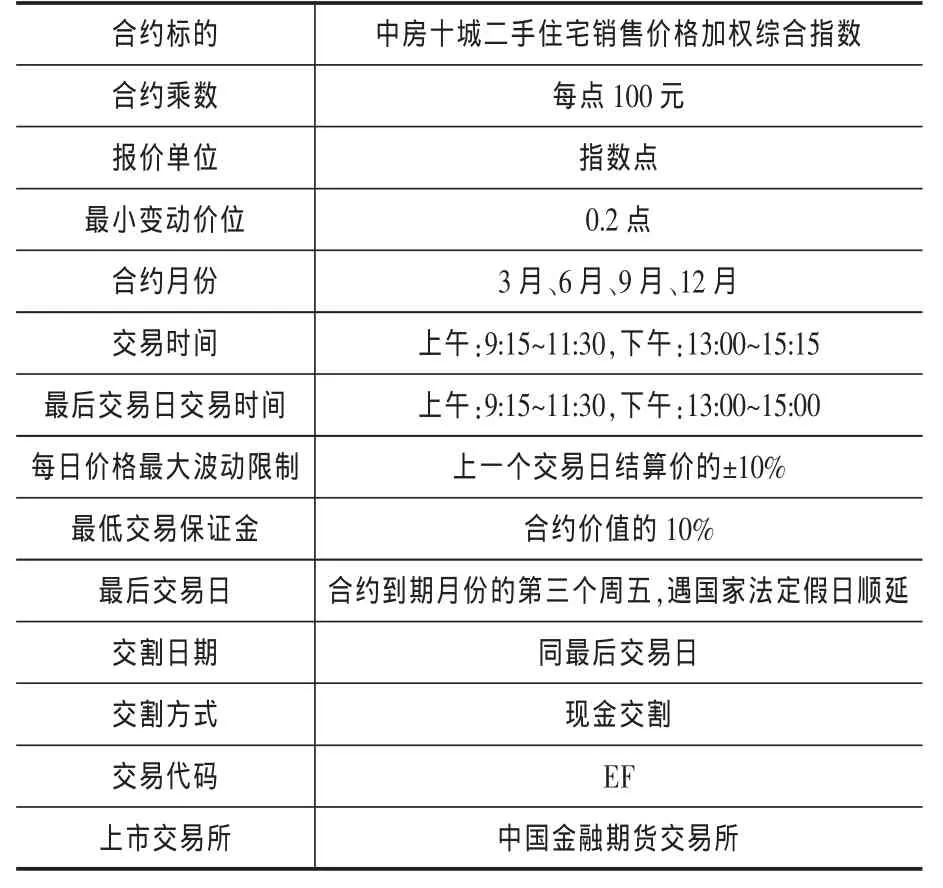
表3 中国房地产价格指数期货合约表

三、中国房地产价格指数期货定价研究

（一）房地产金融衍生品定价理论模型

本文运用Fabozzi等(2012)提出的房地产金融衍生品定价理论，该理论是运用等价鞅测度及风险中性定价方法，基于Harrison等(1981)的连续鞅的随机积分理论提出的均值回归连续模型，以下简称F－S模型。

通过等价秧测度来实现风险中性定价模型方程：

WtQ是一个等价鞅测度下的维纳过程，λ是风险溢价。

该方程的解为：

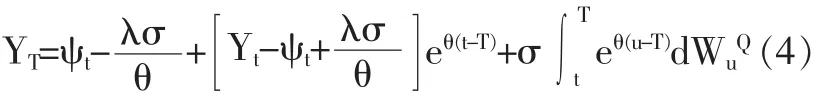
因此，可得：

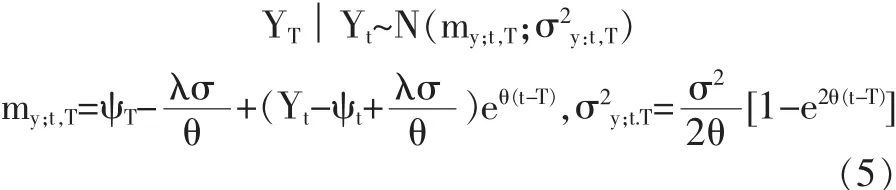
定义到期日为 T′的期货在时刻的 t′价格为 F（t′，T′），F（t′，T′）=Et′Q[XT′]，利用对数正态分布，期货价格方程为:

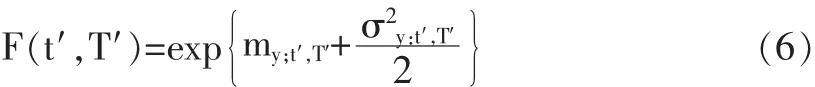
（二）数据选取与分析

由于中国指数研究院于2005年对中国房地产价格指数的编制进行改进与优化，所以本文分别选取中国房地产价格指数系统下的北京、上海、广州、深圳2005年1月至2015年5月新房价格指数中的城市综合指数月度数据，由于F-S模型框架下期货定价模型的参数估计需要，将选取的指数数据转化为对数形式，再进行去除时间趋势的处理，得到符合模型要求的观测变量。

为了对比中国房地产价格与西方国家房地产价格的特点，对选取的城市综合指数月度数据进行相关性分析。将北京、上海、广州、深圳2005年1月至2015年5月新房价格指数中的城市综合指数月度数据分别进行对数差分转化为房地产价格的收益率数据，再观察自相关、偏自相关系数图。

通过分析四个城市的城市综合指数的自相关与偏自相关系数，中国房地产价格指数基本满足在短期内表现出正自相关，在长期内表现出负自相关这一特征，这与Fabozzi等(2012)关于美国标准普尔凯斯—希勒指数与英国IPD年度财产指数的实证分析结果一致。

（三）模型参数估计

由于极大似然估计量具有一系列良好的性质，如一致性、相合性、渐近正态性等，所以本文采用极大似然估计方法来估计F-S模型中的参数。设有n个观测变量，设参数向量 Φ=（ψt，γ，λ）′，其中 γ=（θ，σ）′，由于长期均值 ψt具有时间趋势，设 ψt=α+βt用趋势模型下的最小二乘估计（OLS）方法来估计参数α和β，估计结果如下图所示：

图1 北京城市综合指数对时间趋势的线性回归结果

图2 上海城市综合指数对时间趋势的线性回归结

图3 广州城市综合指数对时间趋势的线性回归结果

图4 深圳城市综合指数对时间趋势的线性回归结果

由于中国尚未建立房地产金融衍生品市场，风险溢价λ采用王建飞（2013）的方法，根据资本资产定价模型，将中国房地产行业板块股票的β系数与沪深300指数期货的收益率和无风险利率的差相乘得出风险溢价λ的值为4.71%。

对于参数向量为 γ=（θ，σ）′，根据公式（5）可得，在F-S模型中给定Yt=x0，YT=Yt+△=X的转移密度函数为：

其中△表示时间区间,由于选取的为月度数据，故=1/12，假设我们在时刻｛t=i△│i=0，1，…，n｝抽样得到n+1个Yt样本观测变量，根据扩散过程的马尔科夫性质，给出F-S模型的对数似然函数如下：

从而，根据(7)和(8)式及观测 到的样本 Y1，Y2，…，Yn， 模型的参数向量 γ=（θ，σ）′可以使用极大似然方法估计，即求解如下的最优化问题：

其中Θ表示参数空间。

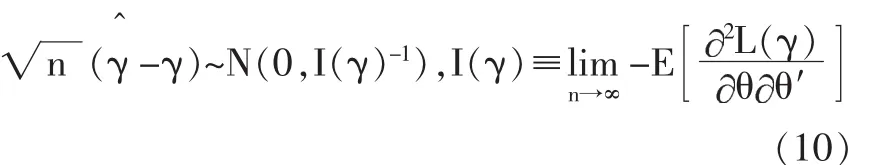
其中I（θ）是信息矩阵。

F－S模型的参数估计结果如下：

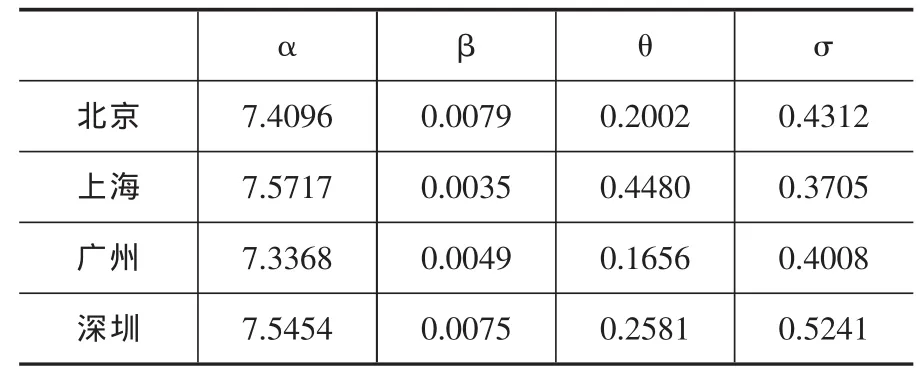
表4 F－S模型参数估计结果

由参数估计结果发现,波动参数σ深圳＞σ北京＞σ广州＞σ上海，说明在2005年1月至2015年5月期间，深圳房地产价格的波动最大，其次依次是北京、广州和上海，可以得出在房地产投资风险方面，深圳的投资风险最大，而上海的投资风险较小。均值回归速度θ上海＞θ深圳＞θ北京＞θ广州， 说明在 2005年 1月至 2015年5月期间，在房地产市场价格面临市场冲击时，上海房地产市场的恢复能力最强，其次依次是深圳、北京和广州。

（四）实证分析

根据前文设计的中国房地产价格指数期货合约中的合约月份与最后到期日，假设现在为2015年6月19日，合约到期日为2015年9月19日，时间间隔为三个月，期货价格公式（6）经过整理得：

将前文估计出的北京市的相关参数：α=7.4096，β=0.0079，θ=0.2002，σ=0.4312 代入公式（11），计算出北京市新房价格指数期货的价格指数点为4109点，根据已设计的房指期货合约的合约乘数为100元每点，得到北京市新房价格指数期货的合约价值为410900元，以此类推，上海、广州和深圳的新房价格指数期货的指数点分别为2905、2575和4543点，合约价值分别是290500元、257500元和454300元。

四、结论

期货作为金融衍生品的重要组成部分之一，具有发现价格、管理风险、套期保值、优化资源配置等功能。近年来中国房地产价格不断攀升，其重要原因在于大量炒作资金的涌入以及只能做多的单边市场机制，在行政手段调控力度的效果逐渐减弱的情况下，作为房价调控手段的补充并依靠市场作用的中国房地产价格指数期货的提出，在多空双边交易机制下，将有利于引导资金进入房地产衍生品市场，分流房地产市场的资金，从而平抑当前房价，使房价回归理性；另外也能够缓解房地产信贷市场的压力，有利于化解银行房贷风险，稳定金融安全；同时也能为投资者拓宽理财渠道，有利于其管理风险。

在此背景下，本文采用Fabozzi(2012)提出的房地产价格指数期货定价模型，结合中国目前具有代表性和权威性的中房指数系统下的新房价格指数，并给出了该模型中参数估计的具体方法，即极大似然估计法，从估计的参数结果中得到两个重要结论：（1）2005年 1月至2015年5月，深圳房地产价格的波动最大，其次依次是北京、广州和上海，从而间接地体现出在房地产市场投资风险方面，深圳的房地产投资风险最大，其次是北京与广州，上海的房地产投资风险最小。（2）2005年1月至2015年5月，上海房地产市场的对市场冲击的恢复能力最强，其次依次是深圳、北京和广州。两个结论可以为房地产投资者提供重要的参考，从而更好地管理投资风险。最终，将估计的参数代入房指期货定价方程，得到理论价格，为中国将来房指期货的推出奠定理论基础。

[1]Case,K.E,Shiller,R.J.and Weiss,A.N,Index－based futures and options trading in real estate[J].Journal of Portfolio Management,Vol.19,1993,pp.83～92.

[2]Case,K.E.and Shiller,R.J,Mortgage default risk and real estate prices:the use of index based futures and options in real estate [J].Journal of Housing Research,Vol.7,1996,pp.243～58.

[3]Fisher,J.D,New strategies for commercial real estate investment and risk management[J].Journal of Portfolio Management,Vol.32,2005,pp.154～61.

[4]Buttimer,R.J,Kau,J.B.and Slawson,C.V,A model for pricing securities dependent upon a real estate index[J].Journal of Housing Economics,Vol.6,1997,pp.16～30.

[5]Bjork,T.and Clapham,E.,On the pricing of real estate index linked swaps [J].Journal of Housing Economics,Vol.11,2002,pp.418～32.

[6]Otaka,M.and Kawaguchi,Y,Hedging and pricing of real estate securities under market incompleteness[J].MTB Investment Technology Institute Co,Ltd.,2002,Tokyo.

[7]Geltner,D.and Fisher,J,Pricing and index considerations in commercial real estate derivatives[J].Journal of Portfolio Management.Special Real Estate Issue,2007,pp.99～117.

[8]Patel,K.and Pereira,R,Pricing property index linked swapswith counterparty default risk[J].Journal of Real Estate Finance and Economics,Vol.36,2008,pp.5～21.

[9]Bjork,T.and Clapham,E,On the pricing of real estate index linked swaps [J].Journal of Housing Economics,Vol.11,2002,pp.418～32.

[10]Baran,L.C,Buttimer,R.J.and Clark,S.P,Calibration of a commodity price model with unobserved factors:the case of real estate index futures[J].Review of Futures Markets,Vol.16,2008,pp.455～69

[11]Schwartz,E.S.and Smith,J.E.,Short termvariations and long－term dynamics in commodity prices[J].Management Science,Vol.46,2000,pp.893～911.

[12]Ciurlia,P.and Gheno,A.,A model for pricing real estate derivatives with stochastic interest rates[J].Mathematical and Computer Modelling,Vol.50,2009,pp.233～47.

[13]Cao,M.and Wei,J.,Valuation of housing index derivatives[J].Journal of Futures Markets,Vol.30,2010,pp.660～88.

[14]Fabozzi,F.,R.J.Shiller and R.Tunaru, A Pricing Framework for Real Estate Derivatives[J].European Financial Management,Vol.18,No.5,2012,762～789.

[15]Harrison,M.J.and Pliska,S.R.,Martingales and stochastic integrals in the theory of continuous Trading[J].Stochastic Processes and Their Applications,Vol.11,1981,pp.215～60.

[16]Lo A W.Maximum likelihood estimation of generalized Ito processes with discretely sampled data[J].Econometric Theory,1988,4:231～247

[17]周佰成，王建飞.基于OU过程的中房指数期权定价[J].管理世界,2013,(4):176～177.

[18]王建飞.中国房地产市场金融衍生品定价研究[D].吉林：吉林大学,2013.

[19]庞丽艳,王建飞,沈思.中国房地产市场金融衍生品定价研究[J].经济纵横,2013,(8):102～105.