考虑分布式电源和需求侧响应的配电网综合规划*

陈伟坚，邹浩斌，王增煜，陈皓勇，罗 波

（1.广东电网有限责任公司清远供电局，广东清远 511500；2.华南理工大学电力学院，广东广州 510640）

0 引言

传统能源的紧缺以及环境污染问题的日益加剧促使电力行业越来越多地关注新能源和可再生能源发电。作为新型的、极具发展潜力的发电和能源综合利用方式，分布式电源技术具有能源类型多样、运行方式灵活、环境效益良好、投资见效明显等优点，能够满足配电网内分散的能源分布和负荷需求，同时还能用于负荷峰谷平衡、提高系统运行可靠性、降低能耗、热电联供、边远地区独立发电。因此，世界电力行业与学术界普遍认为，传统大电网与分布式电源(Distributed Generation，DG)相互结合渗透是21世纪电力工业的发展方向[1-2]。

随着分布式电源对配电网的渗透率逐步增加，受到气象条件等随机性因素的影响，分布式电源的间歇性出力特性将对配电网的安全可靠、经济运行、电能质量等方面造成影响[3-5]。若分布式电源的选址定容不合理，将导致配网潮流分布不合理、运行损耗增大、电网可靠性降低、电压水平不合格等问题。同时，为了促使用户根据实时供用电情况改变电力消费行为，提高电网运行的灵活性，应对DG并网带来的不确定性，适当地引入需求侧响应（Demand Side Response，DSR）机制也是有必要的。

针对含分布式电源的配电网电源规划问题，国内外学者已开展了相关研究。其中，文献[6]在接入分布式电源容量确定的前提下，通过解析法确定了辐射型配网下分布式电源的最佳接入节点。文献[7]综合考虑分布式电源投资费用、网损构造了含分布式电源的配电网规划模型，并采用自适应遗传算法进行寻优求解。文献[8]引进了光伏电站、风电机以及燃气轮机发电三种类型的分布式的电源到规划数学模型中，同时利用粒子群寻优算法来确定DG的选址定容问题。文献[9]基于电源、电网以及负荷三者的综合响应，提出了新能源接入电力系统情景下的整体解决方案，指出未来智能电网的发展需要重点关注分布式电源技术以及需求侧响应技术。但是，考虑分布式电源和需求侧响应的配电网规划还有待进一步研究。

本文在传统配电网规划方法的基础上，为了体现同时引入DG和DSR后对配电网规划的影响，建立基于DG和DSR（这里主要指可中断负荷）的综合规划框架。通过采用快速辐射型配网潮流计算方法，计及DG的投资和年运行费用、环境效益、系统网损、可中断负荷补偿费用、环境效益等建立目标函数，采用基于支持向量机和粒子群算法的混合智能算法优化DG的位置和容量，并获得最佳需求侧响应方案。最后，基于我国某地区实际42节点配电系统3种方案进行经济性比较。

1 基于DG和DSR的综合规划数学模型

随机机会约束规划(Stochastic Chance-Con⁃strained Programming，SCCP)是由Charnes和Cooper提出的[10]，是随机规划领域的重要内容，可在一定的置信水平下求解含有多个随机参数的随机规划问题。在机会约束规划模型中，考虑到随机因素的变化对会约束条件满足度和目标函数值造成影响，需根据实际问题给出目标函数和约束条件的置信水平，使得决策结果使约束条件成立的概率不小于这一水平，避免了资源的冗余配置。

随机机会约束规划模型一般可表示为：

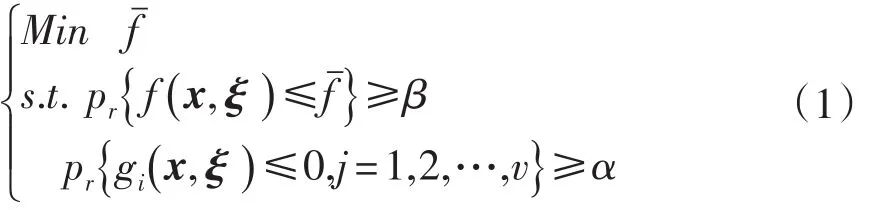
其中，x，ξ分别是决策、随机向量，pr{}·是事件的概率，α、β是决策者预先给定的置信水平， fˉ是目标函数 f( )x,ξ在置信水平至少为β时所取的最大值。

1.1 目标函数

本文综合考虑折算到每年的DG的投资及运行费用、网损费用、可中断负荷补偿费用、引入综合规划后节约的购电费用、环境效益这几个方面确定目标函数，而约束条件包括线路传输容量约束、可中断负荷大小及时长约束、分布式电源接入容量约束以及系统节点电压约束。

本文的优化目标为：

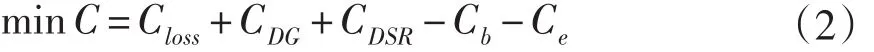
式（2）中的Closs表示系统年网损费用，CDG表示分布式电源投资费用和年运行费用，CDSR为可中断负荷补偿费用，Cb为节约的购电费用，Ce表示环境效益。

（1）系统网损费用

该部分费用为系统的有功网损引起的，即

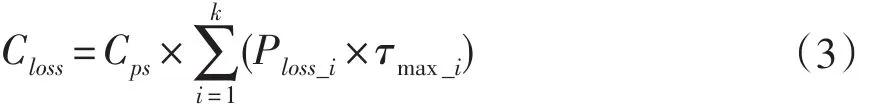
其中Cps为单位售电电价（元/kWh），k为配网系统的总支路数，Ploss_i为第i条支路的有功网损功率，τmax_i为第i条支路的年最大负荷损耗小时数。

（2）分布式电源投资费用和年运行费用

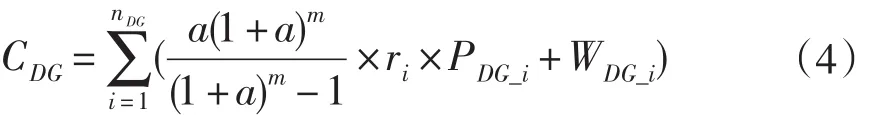
其中nDG为DG个数，a为贴现率，m为DG的使用年限，ri为在节点i接入单位容量DG的投资费用，PDG_i为节点i处接入DG的容量，WDG_i为在节点i处接入DG的年运行维护费用。

（3）可中断负荷补偿费用

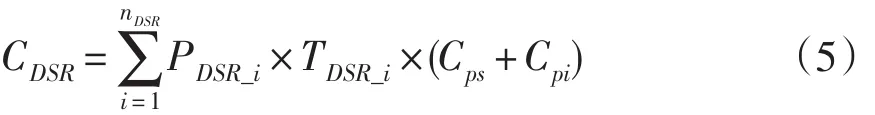
其中nDSR为可中断负荷用户数，PDSR_i和TDSR_i分别为第i个可中断用户的履约中断负荷以及中断时间，Cpi为可中断负荷的单位补偿费用。

（4）节约的购电费用

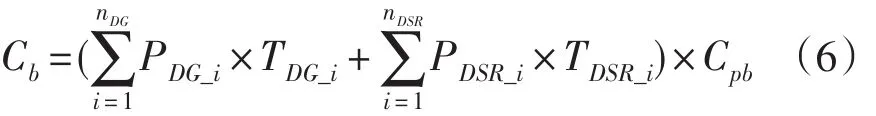
其中TDG_i为第i个分布式电源的年利用小时数，Cpb为单位上网电价。

（5）环境效益

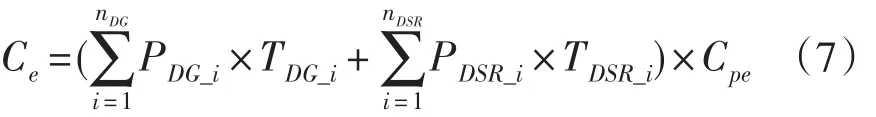
其中Cpe为由常规火力发电厂供电的单位电量的环境成本。火力发电的污染物主要有二氧化硫（SO2）、氮氧化合物（NOx）、二氧化碳（CO2）、一氧化碳（CO）、总悬浮颗粒物（T SP）、粉煤灰和炉渣等。

1.2 约束条件

（1）潮流等式约束

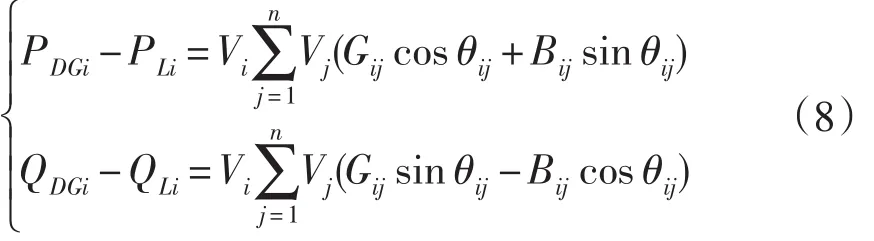
其中 PWPGiPWPGi,QWPGi、QWPGi为 PLi节点i所接风力发电机的有功、无功输出；PLi,QLiQLi为节点i处的负载功率；ViVi为节点i的电压幅值，GijGij为支路电导， BijBij为支路电纳,θijθij为节点i与节点 j电压相角差。

（2）电压上下限约束

其中Vmax和VminVmin,Vmin分别为节点i电压的上下限。

（3）支路潮流约束

其中Smaxj为支路 j上线路容量的限值。

（4）可中断负荷约束

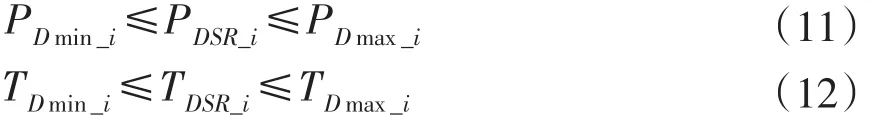
其中 PDmax_i、 PDmin_i和TDmax_i、TDmin_i分别为第i个可中断用户与供电企业都愿意接受的中断负荷上下限和年累计中断时间上下限。

（5）待选节点分布式电源装机容量约束约束

其中SDGi为第i个待选节点接入分布式电源容量，SLi为第i个待选节点允许安装的分布式电源的最大容量。这里规定分布式电源在某个节点上的接入容量小于该节点最大负荷的20%。

2 混合智能算法

近年来粒子群算法（particle swarm optimiza⁃tion，PSO）在电力系统优化问题中得到广泛应用，但若直接利用PSO算法求解含分布式电源的配电网综合规划数学模型，种群中每个粒子进行适应度计算时，需先计算通过随机模拟技术产生的各随机场景的适应度值，然后依据决策者给定的目标函数置信水平确定各粒子的适应度值，从而进行种群的迭代寻优。当随机场景数较大时，粒子群迭代寻优时所需进行潮流计算的次数将变得相当庞大，直接导致综合规划模型的寻优求解效率低下[11]。

而在实际工程应用中，算法的执行效率是一个非常重要的问题，实际上需要的是比较各个解的相对优劣性，在求解过程中计算解所对应的目标函数精确值并无必要，可寻求近似估计算法。

支持向量机（support vector machine，SVM）这一新颖的智能算法在函数逼近中已取得不错的逼近效果[12]。为了减少系统潮流计算次数以达到提高求解速度的目的，本文根据随机模拟技术产生足够的训练样本，并采用支持向量机良好的拟合泛化能力对这些训练样本进行拟合，形成支持向量机回归拟合函数，并用它代替费时的潮流计算过程，在进行粒子群寻优过程中直接用支持向量机回归拟合函数进行适应度估计。

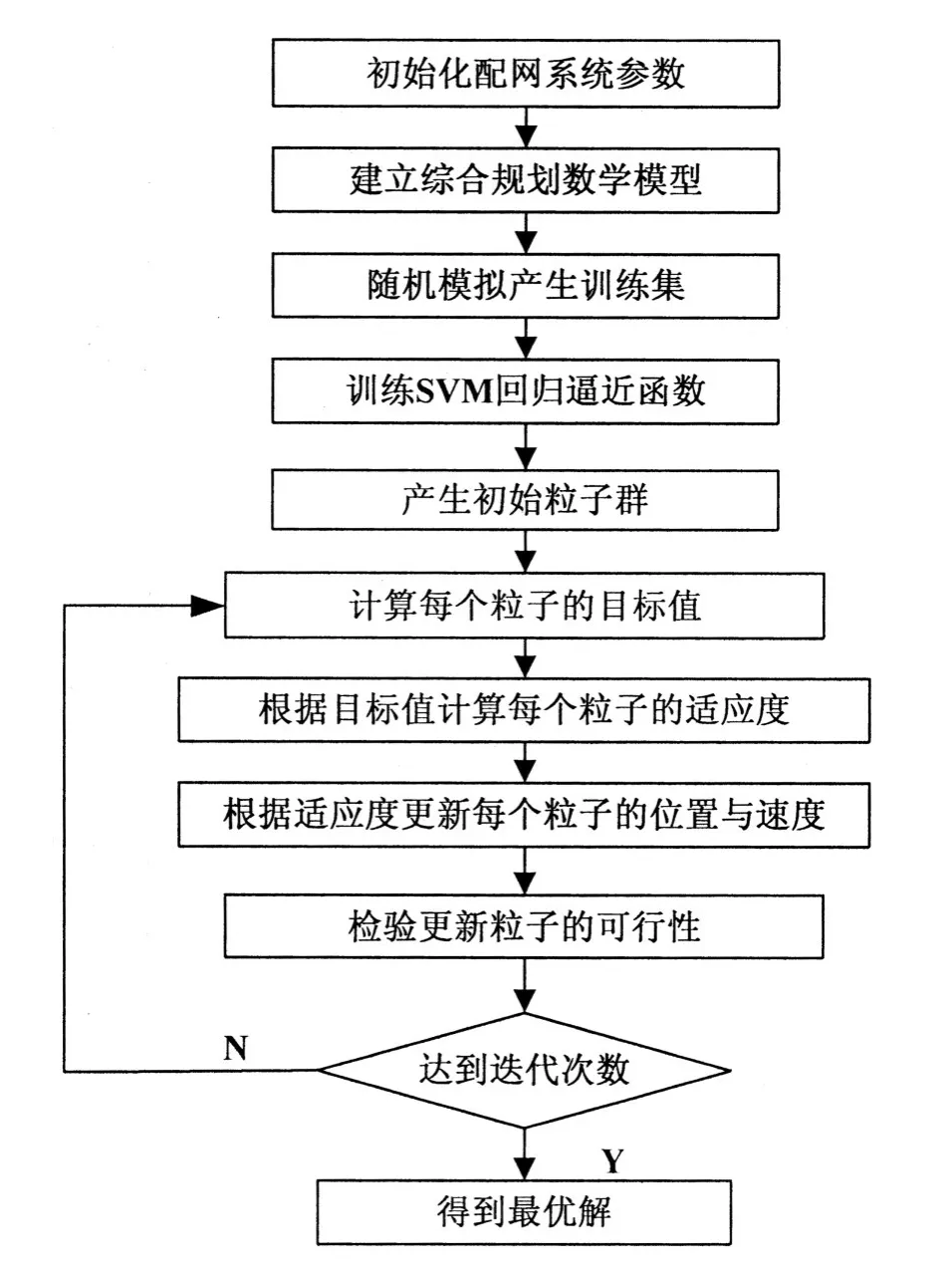
图1 混合智能算法流程图

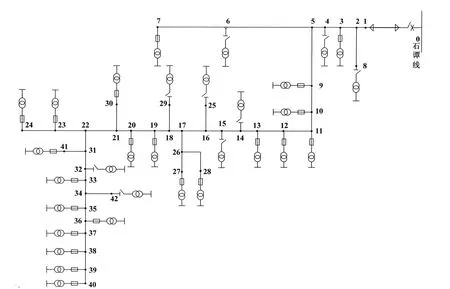
图2 某地区配电网接线图

因此，文本利用混合智能算法（hybrid intelli⁃gent algorithm，HIA）求解含DG与DSR的配网综合规划问题，流程如图1所示。

3 案例分析

本文以我国南方某地区实际配电网（42节点）为例进行分析计算，该配网接线图如图2所示。所有线路总长度为26 km，总用户数为5 947个，其中含7个工业用户，2个电站用电负荷，5 938户农村或商业用户，某化工厂为该线的最大工业负荷，年最大负荷达到1 737 kW，其余工业用电负荷均小于400 kW，这里选择某化工厂作为可中断负荷进行需求侧管理。

假定中断负荷单位电量补偿费用为0.6元/kWh，售电电价为0.74元/kWh，火电机组上网电价为0.48元/kWh，传统发电厂的总环境成本为0.117 1元/kWh[13]，单位容量风机的投资购买费用为6 300元/kW，假设风机的运行寿命为25年，贴现率为0.1，粒子群优化算法种群规模为20，迭代次数取为500，每个训练样本的风速场景随机模拟个数为200，支持向量机的训练样本个数为2 500。

为了检验混合智能算法的准确度及求解效率，本文先利用随机模拟与PSO算法相结合的随机机会约束规划算法对该配电网进行综合规划，其中随机风速样本取为200，目标函数置信水平β为0.5，电压约束条件置信水平α为0.95，粒子群规模设为20，迭代次数为200。另外，根据图1所示的流程图，利用混合智能算法求解该相同问题，在为支持向量机回归拟合模型产生训练样本时，训练样本数取为1 250，两种算法的优化结果如表1所示，在DG优化方案中，括号前的值为DG接入的节点号，括号内的为接入DG的容量（单位为kW）；在可中断负荷方案中，括号前的值代表供电企业与某化工厂拟定的可中断负荷大小（单位为kW），括号内的则为中断时间（单位为h）。

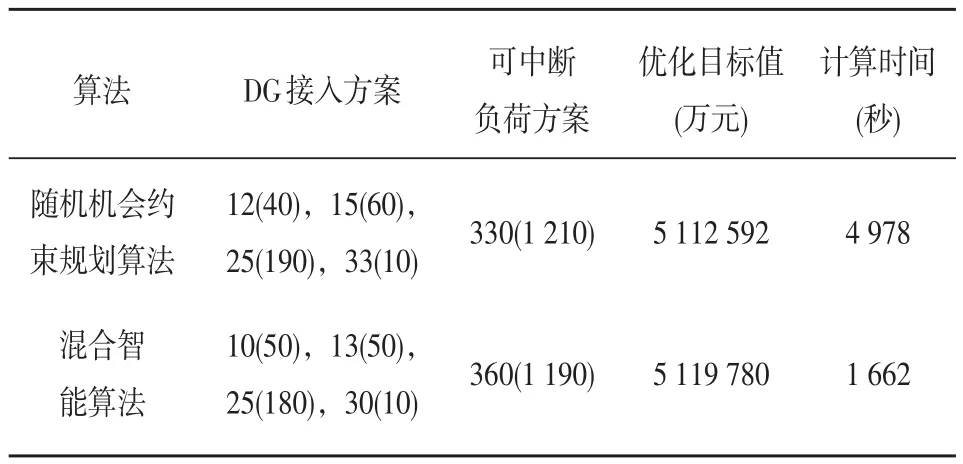
表1 优化结果比较

从表1可看出，与传统的随机机会约束规划算法相比，利用混合智能算法求解得到的优化方案亦能达到较好效果，最优目标值的相对误差只为0.14%，因回归逼近函数造成的计算误差仍在容忍范围内。同时，由于避免了在PSO寻优迭代过程中对每一代的每个粒子都进行潮流计算，只需在为支持向量机回归拟合模型产生训练样本时进行次数较少的潮流计算，计算时间由4 978秒缩短到1 662秒，减少到原先的33.38%，大大提高了求解效率。

为研究基于分布式电源接入与可中断负荷管理的配电网综合规划的经济性和可靠性，利用混合智能算法分别求解了三种情况下的规划方案，在第一种情况下不考虑DG接入与可中断负荷管理，而第二种场景下仅考虑DG接入，第三种场景则同时考虑DG及可中断负荷进行综合规划，规划方案费用对比如表2所示。

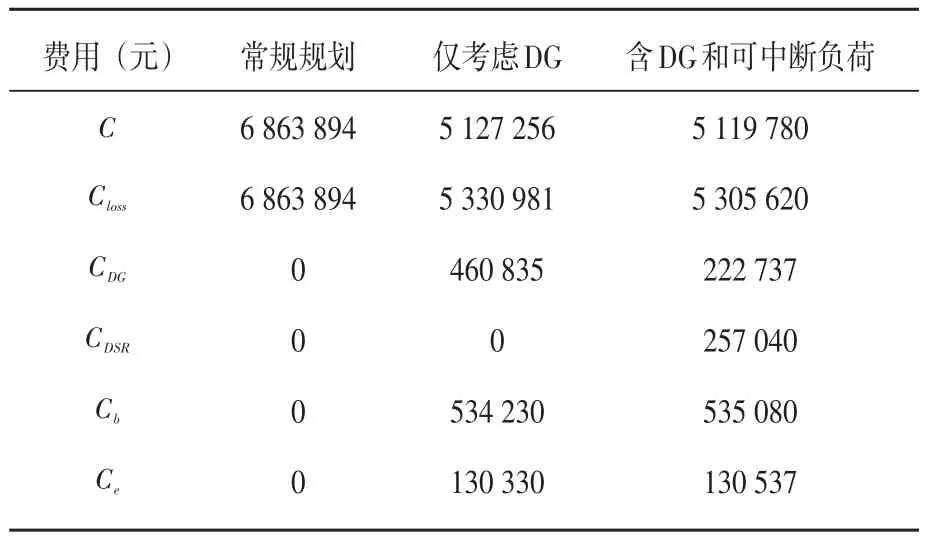
表2 三种规划方案费用比较

从表2可知，在对配网进行综合规划后，可部分消除电网过负荷和线路阻塞，提高电网的输电容量裕度，减少网损费用和配网线路扩建支出。尤其面对全球能源紧缺的现状，DG能够实现环境友好型的绿色环保发电，可中断负荷则有利于推动节能减排工作开展，带来相当的环境效益。同时，随着DG技术的发展，其购买安装成本将逐步降低，含DG及可中断负荷综合规划方案的经济优势会越来越明显。

4 结论

本文建立了基于机会约束规划的含DG及可中断负荷的配电网综合规划数学模型，并利用随机模拟技术仿真风机各种出力状态，同时避免确定性约束条件造成优化结果过于保守。为了提高计算速度，采用支持向量机与粒子群算法相结合的混合智能算法进行求解，避免大量重复的潮流计算，并取得较好的计算精度。基于某地区实际配电网数据的计算结果表明该算法有效可行，具有较高的工程应用价值。对不同情况下的规划方案的经济性和可靠性指标对比分析表明，含DG及可中断负荷的综合规划方案能减少或推迟峰荷配电网线路扩容建设，提高负荷率，带来相当的环境效益，同时能弥补DG间歇性出力特性的缺陷，减少DG接入容量，提高系统供电可靠性。

［1］张勇，吴淳.分布式发电机在配电网中的优化配置［J］.电力系统保护与控制，2010，38（11）：33-34.

［2］黄庆云.含分布式电源的配电网固定成本分摊［J］.机电工程技术，2014（6）：182-185.

［3］韦钢，吴伟力，胡丹云，等.分布式电源及其并网时对电网的影响［J］.高电压技术，2007，33（1）：36-40.

［4］钱科军，袁越.分布式发电技术及其对电力系统的影响 ［J］.继电器，2007，35（13）：25-29.

［5］宋祺鹏，宋晓辉，杨亮.分布式电源对配电网规划的影响［J］.电气时代，2010（4）：74-75.

［6］Griffin T，Tomsovic K，Secrect D，et al.Placement of dispersed generation systems for reduced losses［C］.Proceeding of the 33rd Hawaii International Conference on System Sciences， Maui （Hl，， USA）， 2000：1446-1454.

［7］邱晓燕，夏莉丽，李兴源.智能电网建设中分布式电源的规划［J］.电网技术，2010，34（4）：7-10.

［8］庄雷明.城市电网规划中分布式电源容量的优化配置［D］.北京：华北电力大学，2010.

［9］刘吉臻.大规模新能源电力安全高效利用基础问题［J］.中国电机工程学报，2013，33（16）：1-6.

［10］ Charnes A，Cooper W W.Chance-constrained Pro⁃gramming［J］.Management Science，1959，6（1）：73-79.

［11］李爱国，覃征，鲍复民，等.粒子群优化算法［J］.计算机工程与应用，2002，38（21）：1-3.

［12］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26（1）：32-42.

［13］俞海淼，周海珠，裴晓梅.风力发电的环境价值与经济性分析［J］.同济大学学报：自然科学版，2009，37（5）：704-708.