重建基于小组合作学习的数学高效课堂

吴子林

(连城县实验小学，福建 连城 366200)

重建基于小组合作学习的数学高效课堂

吴子林

(连城县实验小学，福建 连城 366200)

阐述小组合作学习的方法：巧妙分组，追求组员之间的合作；巧妙分工，促进组员之间的合作；巧妙组织，让学生在合作中求知、发展。在“容易产生认知冲突的内容、开放性的内容和个人无法独立完成的内容”时要安排小组合作学习；要真正留足小组合作学习的时间和组际交流的空间，让学生在合作中学会学习，在学习中学会合作，在合作中发展。

重建；小组合作学习；高效

自课程改革以来，小组合作学习成为区分新课改课堂与传统课堂教学的一个最明显特征之一。它有力地改变了传统课堂上教师“一言谈”的专制，在课堂上给学生以自主、合作的机会，培养了学生的组内团体合作意识和组间良性竞争意识，发展了学生的人际交往与分辨的能力。高效的小组合作学习，能使小组成员之间相互促进，形成开放、互补、包容的学习氛围；能提高学生的学习效率和学习兴趣，增强学生的人际交往能力。小组合作学习虽然在当今课堂得以广泛使用，但是在实际操作中却一直存在着种种问题。如何重建基于小组合作学习的小学数学高效课堂，值得深思。

一、巧分组，追求组员之间的合作

1.合理搭配。就是把学习成绩优劣、能力强弱、性别不同、性格和家庭背景有差异的学生分在一个小组内，注意男女生的人数要相对均衡，学优生、中等生、学困生的比例尽量做到1∶2∶1，使小组成员间保持一定的差异。由于每个小组都是异质的，所以就连带产生了全班各小组间的同质性，达到“组间同质、组内异质”。[1]

2.动态分组。合作学习中的分组如果一直是固定结构，时间一长，就会使学生的参与兴趣降低，因此可以通过动态分组进行调节。动态分组主要有自愿分组和按见解的不同随机分成观点不同的正、反两组：自愿分组能调动学生的积极性，活跃课堂气氛；分正、反组可以形成两大阵营，让学生更好地针对某一问题或观点进行有效的辩论。

二、巧分工，促进组员之间的合作

合作学习特别强调每个人在小组合作中的责任，要使每个人都认识到，他们不仅要为自己负责，而且还要为小组的其他同伴负责。组员之间只有互相依赖，互相帮助，拧成一股绳，才能很好地完成合作学习的任务。

1.小组规模。学习小组的规模是不确定的。小组的人数，一般为4～6人。一开始，教师应有意识地安排2人小组，完成一些简单的合作任务，让学生慢慢学会合作。当学生已经初步学会小组合作学习，这时候小组的规模可适当加大。3人或4人合作学习，对空间场地的变化要求不是很高，较容易实现。

2.座位安排。小组合作学习时，要根据教学的内容和教学活动的组织形式将单一的“秧田式”座位进行适当变化。如讨论、实验等采用“风车型”“餐桌型”“口字型”，游戏、表演时采用“扇形”“马蹄型”“U字型”，操作、竞赛等采用“餐桌型”“品字型”“U字型”“梅花型”。[2]每个小组都要安排教师的座位，方便教师指导小组学习活动，拉近生生、师生之间的距离，建立起民主平等的师生关系，增加师生间、生生间交往的密度。

3.角色分配。小组组建后，不一定会出现教师预期的合作效应。小组内应分工明确，每一位学生都要在小组中担任特定的角色：小组长，负责小组合作的组织和分工，保证每个人都有参与和表现的机会，组织有序地交流讨论，防止“一哄而上”，最重要的是引导其他组员认真倾听和补充，并根据组员在合作学习时参与度、学习态度等给组员评分；记录员，负责记录合作学习中小组的发现和小组讨论的结果；材料管理员，负责领取和保管小组合作所需要的材料，确保合作有序进行；发言人代表小组在全班交流小组的研究成果。这样，小组成员分工合作，共同实现小组目标。在学生已学会合作的基础上，也可实行“角色轮换”，鼓励每个成员在不同的角色中充分展现自己，使学生在合作中取长补短，促进知识、技能的迅速提高。另外，由于每个小组都有一个学习相对更困难的学生，所以还要给他安排一位学优生做他的“师傅”，“面对面”“一帮一”地帮助学困生。这样，让其他学困生也能跟上小组合作学习的步伐，达到共同进步的目的。

三、巧组织，让学生在合作中求知、发展

《义务教育数学课程标准(2011年版)》指出：“数学活动是师生积极参与、交往互动、共同发展的过程。学生是数学学习的主体，教师是数学学习的组织者与引导者。”[3]在学生的合作学习时，教师虽然由台前退到幕后，但是必须为学生搭建合作平台，努力营造全员参与的生动活泼的合作氛围。

1.合理安排合作学习的内容，让学生在合作中求知

并不是所有的内容都需要学生合作学习的。选准、选精学习内容是确保合作学习实效性的重要因素。对于较简单的学习内容，学生可以独立自学或者由教师进行一般性教学；而相对复杂、需要探究的综合性学习内容，则鼓励学生采取合作学习的方式。

(1)容易产生认知冲突的内容。容易产生认知冲突的内容，让学生口欲言而不能的问题，最值得合作学习。[4]针对学生在学习中产生的认知冲突，教师适时引导学生进行讨论、辨析，让学生在争论中逐渐自悟，从而体现合作学习的价值。

(2)开放性的内容。一些具有开放性的问题，或者可用多种方法、多种策略解决的问题，是学生进行合作学习的很好资源。[5]笔者在教学“梯形面积的计算”时，学生能利用前面所学的平行四边形和三角形面积公式推导的方法，用两个完全一样的梯形拼成一个平行四边形推导出梯形面积公式。这时我问“还能不能用其他方法推导出梯形面积计算公式呢？”学生在独立观察、思考后，通过小组合作、动手操作，纷纷探索出不同的解决方法：有的将一个梯形分成两个三角形(如图1)，得出S=ah÷2+bh÷2=(a+b)h÷2；有的将梯形剪、拼成三角形如图(2)，得出S=(a+b)h÷2；有的将梯形分成一个平行四边形和一个三角形(如图3)，得出S=ah+(b-a)h÷2=ah+bh÷2-ah÷2=ah÷2+bh÷2=(a+b)h÷2；有的将梯形沿两腰的中点剪开，旋转后拼成一个平行四边形(如图4)，得出S=(a+b)(h÷2)=(a+b)h÷2。这样在合作交流中，既充分挖掘了每个学生的探究潜能，又培养了学生合作学习能力。

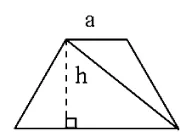
图1

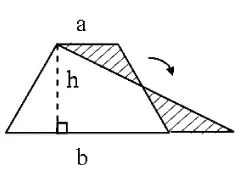
图2

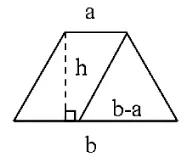
图3

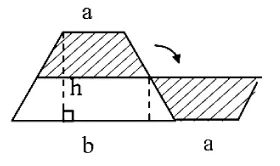
图4

因为不同学生的知识基础、能力、兴趣、爱好等都是不尽相同的，每个学生思维的角度都可能不一样，开放性的问题必然会引发学生多维度的思考，小组合作学习就能有效地实现互补。

(3)靠个人力量无法独立完成的内容。当出现学生个人无法独立完成、需要同伴的帮助才能完成的学习内容时，要组织小组合作学习。[6]如教学“统计”时，教师预设了“统计‘六一儿童节’班级联欢会所需要购买的水果、茶点”的情境，由于人数多，每人所需要的品种数目、数量也多，学生自己独自一个人统计一时忙不过来，这正达到教师所需要的效果——让大家想到要寻求同伴的帮助，进行小组合作。然后组建学习小组，进行分工：有的统计苹果的数量，有的统计香蕉的数量，有的统计瓜子的数量，有的统计花生的数量……一个一个记太慢，就画“正”字来表示。好办法在学生你一言我一语中就出现了。这样，既让学生亲历统计过程，体验合作的威力，让学生真正明白“为什么要合作”和“怎样进行合作”。

2.真正留足合作学习的时空，让学生在合作中发展

学生在教师的引导下独立思考、自主探究的过程中总会发现问题，得出自己个性化的结论。对发现的问题总是希望得到同伴的帮助，对自己的发现更是想展示于众，得到大家的验证、肯定和赞扬。在教学过程中，教师要真正为学生留足合作学习的时空，以促进学生的发展。

(1)留足小组合作的时间。维果茨基提出了“最近发展区”，就是学生即将获得并能够获得的经验，但这种经验现在暂时还不具备。学生通过自学后还不明白的问题，就是处在学生各自最近发展区的问题，教师应为学生留下足够的合作交流的时间，让学生谈所得、提问题、议发现。

(2)留足组际交流的空间。学生在小组合作学习中，也常会出现“是什么”而说不清“为什么”的“愤悱”状态，这时可允许学生跨组请教。如在教学“三角形的三边关系”时，老师发两根小棒给学生，要求学生用两根小棒摆成三角形。有一个小组议论纷纷，问题在本小组得不到解决，学生就跨组向别组同学请教。通过组际交流，他们知道了用两根小棒摆成三角形必须要再配上一根，才能围成三角形。然后教师再引导学生思考：再配上一根多长的小棒，就能围成一个三角形？有几种配法？这样，不仅使学生学会解决问题的办法，获得学习的经验，还能让学生体验到合作学习的必要性，感受到合作学习给自己和他人带来的快乐。

(3)留足学生争辩的时空。学生在活动交往中，由于思维的不断碰撞，问题不仅越来越多而且越来越尖锐。这时教师可从学生在课堂上生成的疑难问题中，抽取出与本节课有关的、有价值的问题，并提出来组织学生通过争辩来解决。如教学五年级下册数学拓展性知识“互质数”时，教师抽取一个学生质疑的问题：有什么办法很快地判断出两个数是互质数？先鼓励学生独立思考，在学生有了自己的观点、看法的基础上，让学生辩驳。学生甲说：“两个数，其中一个是质数，那么这两个数一定是互质数。”生乙马上反驳说：“6和3这两个数就不是互质数。”生丙又提出：“两个数都是质数，这两个数一定是互质数。”生丁马上说：“3和3就不是互质数，应该说两个不同的质数是互质数。”接下来学生又提了许多问题，如：两个数都是合数，一个数是偶数另一个数是奇数，一个数是合数另一个数是质数，1和任何自然数等等，这样的两个数一定是互质数吗？通过争辩，学生终于弄清了成为互质数的两个数的几种情况，体验到合作学习带来的快乐。

“在合作中学会学习，在学习中学会合作”。有效的合作既是学习取得成功的条件，更是数学高效课堂的保证。重建基于小组合作学习的数学课堂，让学生带着自己的生活经验走进课堂，同教材、教师、同学对话，在小组合作中自主探索，合作交流，亲身体验，生成自己独特的、个性化的见解，获得更多的数学活动经验，获得更多的学习乐趣，促进学习品质的全面提升，这是我们今后在数学教学中不断探索研究的方向。

[1]刘吉林，王坦.合作学习的基本理念(一)[J].人民教育，2004(1).

[2]郭宝珍.数学教学中的“合作学习”[J].山西教育(教学)，2013(2).

[3]教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.

[4]王甲娜.哪些内容适合合作学习[J].基础教育课程，2006(2).

[5]陈清容.为数学合作学习选准内容[J].人民教育，2004(3).

[6]乐华文.选准数学合作内容，确保合作学习实效[J].教育，2009(3).

2014-08-20

吴子林(1971- )，男，福建连城人，连城县实验小学高级教师。

< class="emphasis_bold">文章编号：1673-9884(2015)02-092-04

1673-9884(2015)02-092-04