一种适用于卫星数据传输的高效编解码算法

张亚航 程博文

(北京空间飞行器总体设计部,北京100094)

一种适用于卫星数据传输的高效编解码算法

张亚航 程博文

(北京空间飞行器总体设计部,北京100094)

提出了一种喷泉编解码方法,又称为快速速龙码(RRC),该编码方法能实现与传统速龙码相同的差错控制效率的同时,时间复杂度相对更低。相对传统速龙码,在编码过程中无需计算中间节点,直接通过生成矩阵计算校验节点;其解码方法是先通过置信传播(BP)算法对校验节点进行降度之后,再对校验节点降度之后组成的矩阵进行高斯消元法解码,从而降低矩阵规模。改进后的算法更加高效和简单,适用于航天器空间通信中的应用层数据传输、存储保护和深空探测信号传输。

速龙码;喷泉编解码;空间通信;卫星

1 引言

卫星广播通信覆盖区域广阔,传播距离远,和其他通信方式相比有其独特的优势;特别是在发生重大自然灾害的时候更能表现出其不可替代的通信能力。但是无线通信中由于通信环境的影响(如太阳耀斑干扰),会出现数据在传输中丢失或错误的情况。这个时候需要信道纠错编码进行数据恢复保证数据传输的可靠性[1-2]。

喷泉码[3-4]最大的特点是码率无关性,接收端只要收到比原信息长度略多的码字,就能将所有信息还原。喷泉码的理念由Luby于1998年提出,并在2002年提出了一种具体的喷泉码算法——LT码[4]。其后,Shokrollahi等进一步研究,提出了译码性能更好的速龙码(Raptor Codes)[5],2005年后Luby将其改进为系统速龙码(Systematic Raptor Codes),并在2007年成为RFC(Request for Comments)标准[6]。相对于传统编解码算法,速龙码的优势主要包括:码率无关性;能够以小的冗余、以极高的概率恢复出源节点;只有异或操作,具有较高的效率;源节点大小可以是任意长度;编码冗余动态可调。由于以上特点,该算法能够满足一些航天任务需求,适合航天领域应用。

国内航天器星载计算机运算速度一般在10～50 MHz,软件运行空间较为受限[7]。相对于航天器嵌入式软件运行环境,该算法仍然显得过于复杂,且由于编解码矩阵较大,内存占用较多。文献[8]认为传统速龙码解码过程中从L×L寻找具备r个1的行的过程效率太低,并提出了改进的算法从而提高了解码速率。文献[9]通过增加预处理过程改进生成矩阵,进而减少解码时矩阵行列交互次数,从而提高解码速度。文献[10]通过改进预编码,从而提高译码效率。尽管这些文献在一定程度提高了编码复杂度,但是解码矩阵规模并无变化,只是将解码时矩阵运算简化。

本文通过对传统速龙码的编解码方式进行修改,在编码过程将中间节点和修复节点计算合并成一次矩阵运算,直接通过生成矩阵计算校验节点;其解码方法先进行置信传播(BP)算法对校验节点进行降度之后,再对校验节点降度之后组成的矩阵进行高斯消元法解码,从而降低矩阵规模,使得编解码速率提高,称为快速速龙码(Rapid Raptor Codes,RRC)。试验表明,该算法的编码速率和解码速率相对传统速龙码有了明显改进,同时该算法的解码矩阵规模明显减小。

2 传统速龙码

2.1 编码算法

传统速龙码的编码过程分为两步[6]:

第1步:通过K个源节点生成L(L＞K)个中间节点。假设消息由K个给定的源节点组成,设向量C,有C=[C1,C2,…,CL-K,CL-K+1,…,CL-1,CL],预编码生成矩阵G1L×L。令

式中 M为中间节点向量;L×L的矩阵G 1L×L代表着预编码过程中LDPC、Half码与LT码在伽罗华域GF(2)上的生成矩阵,且保证矩阵G1L×L满秩,即该矩阵可逆。G1L×L的结构如图1所示, S为矩阵G_LDPC的列数;H为矩阵G_Half的列;K标识源节点个数,也是矩阵G_LT的列; L=S+H+K。

第2步:由L个中间节点根据LT编码算法,计算出编码矩阵G2N×L生成N个最终的修复节点向量R=[R1,R2,…,RN],其中,G2N×L每个行代表一个修复节点生成向量,每个列代表一个中间节点。

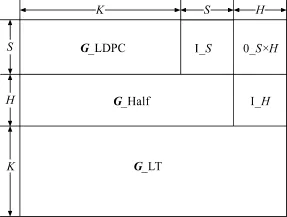
图1 G1L×L结构Fig.1 Composition of G1L×L

2.2 解码算法

传统速龙码解码算法基于高斯消元法。假设接收到P个节点(K≤P≤K+N),接收到的节点集合记为向量D。

第1步:令Q=S+H+P,根据接收到的节点,可以获得Q×L的矩阵G 3Q×L,其中G3Q×L的生成方法见参考文献[6],且有

第2步:对G3Q×L进行高斯消元,若最终G3Q×L转化成L×L的单位矩阵,即G3Q×L的秩大于L,则可以解出M,否则解码失败。

第3步:根据M和方程式(1),可以算出向量C,即源节点。

3 快速速龙码

3.1 编码算法

本设计方案中,在编码过程中不再采用中间节点得到校验节点的方法,而是按照下式直接生成校验节点向量R=[R1,R2,…,RN],从而生成N个校验节点。具体方式如下。

令LT编码算法LTEnc()产生一个N×L的LT编码矩阵G2N×L。矩阵G2N×L的结构如图2所示。

矩阵G2N×L中第i行为1的列代表着相应位置上的中间节点参与了生成第i个校验节点的异或操作,则校验节点R的产生所示为

式中 G2N×L×G1L×L表现了源节点与校验节点应满足的关系。在此记

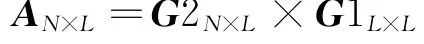
矩阵AN×L中同源结点向量C进行异或的列为后K列,因此取AN×L的后K列构成矩阵ZN×K,可得

图2 G2N×L结构Fig.2 Composition of G2N×L

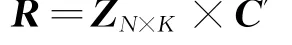
式中 向量C′=[C′1,C′2,…,C′k]代表K个输入节点的集合。如图3所示,Pre_A标识矩阵AN×L的前S+H列,End_A标识矩阵AN×L的后K列。

由上述过程可以看出,相对于传统的速龙码编码方法,本设计方案的编码方法中省去了中间节点的复杂计算,从而大幅度减小编码时间消耗,降低编码器对硬件的要求。

图3 矩阵A与矩阵ZN×K的关系Fig.3 Relationship between matrix ZN×Kand matrix A

3.2 解码算法

如3.1节所示,本算法在编码过程中除去了中间节点的计算,解码算法同样不计算中间节点,而是结合高斯消元算法和置信传播译码算法进行解码。

假设在实际应用场景中,接收端收到K′个源节点和N′个修复节点,且有K′≤K,N′≤N,则丢失的源节点数为k=K-K′,k与信道丢包率β相关,一般来说k=K×β。

本文方案中,将通过置信传播算法和两步完成解码算法及最大似然解码算法相结合的方法进行解码。

第1步:先采用置信传播译码算法进行解码矩阵降度。

如第3.1节所示,修复节点实际上是由一个或多个源节点通过生成矩阵生成。设其中第i个修复节点由di个源节点生成,则称该修复节点的度为di,显然,源节点本身可以看作度为1的修复节点。对所有N′个修复节点的度向量集合为d=[d1,d2,…,dN′]。此时,采用置信度传播算法,对修复节点进行“降度”操作(表示将修复节点同组成它本身的源结点进行异或运算),若d中第i个元素di中包含有已接收到K′个源节点中的元素j,即第j个源结点参与异或运算生成修复节点di,则将di对应的修复节点与第j号源节点进行异或,直到d中不含有K′个源节点中的任意元素。

此处引入节点之间相关的概念,判断第i个修复节点同丢失的源节点j是否相关的方法是:查询矩阵ZN×K,若ZN×K中第i行、第j列为1,则说明第i个修复节点同第j个源节点相关。

第2步:通过最大似然解码(高斯消元)算法完成最终解码。

假设降度之后剩余n个校验节点,n≤N′,则剩余修复节点集合记为R′=[R′1,R′2,…,R′n]。由于降度之后的校验节点只同丢失的源结点相关,取d′中所有度向量构成一个n×k的小矩阵Z′,矩阵Z′的形式如图4所示。其中Z′的第i行为1的列代表着相应位置上丢失的源节点参与了生成校验节点的异或操作。记所有丢失的源节点集合为向量C′=[C′1,C′2,…,C′k]。

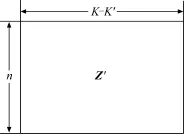
图4 降度之后的Z′矩阵Fig.4 De-degreed matrix Z′

显然,Z′矩阵满足等式

通过最大似然解码算法(高斯消元解码算法),根据式(4),可以解出丢失的源节点向量C′=[C′1,C′2,…,C′k]。从而计算出丢失的k=K-K′个源节点,将计算出来的丢失源结点补充到源数据中,完成数据的修复。

4 性能分析

本节主要针对LT编码、速龙码和快速速龙码进行分析和比较,并对速龙码和快速速龙码进行软件仿真编解码速度比对。

4.1 计算性能理论分析

(1)传统速龙码计算性能分析

速龙码的编码算法中,先通过预编码算法生成中间节点,然后再用LT编码算法进行编码。设K为源节点个数,其编码时间复杂度为O(K ln(1/e)),其中e为编码冗余度。在解码过程中,系统速龙码采用高斯消元法,其时间复杂度为O(K3)。

(2)快速速龙码计算性能分析

速龙码取消了中间节点的生成,其编码时间复杂度为O(δ×K×e),其中δ为编码平均关联度,一般来说δ为2左右。解码算法中,由于结合了高斯消元算法和置信传播译码算法,因此时间复杂度跟丢包率β相关,其时间复杂度为O((βK)3),可见,当β＜1时,快速速龙码无论是编码算法还是解码算法,时间复杂度都大大优于速龙码。

4.2 译码性能理论分析

本系统编码算法的结果同传统速龙码的结果一样可以最大限度地利用修复节点解码,而且解码纠错性能完全一样,证明如下:

根据2.1节编码方案可知,传统速龙码编码方程R=G2N×L×G1L×L×C,等价于本设计中编码时的关系式R=ZN×K×C,对于传送的源节点,将传送的源节点看作在ZN×K之上加入K×K的单位矩阵的编码矩阵为Z 1(N+K)×K,显然,传统速龙码最终能够正确解码的前提是接收到的节点重构的矩阵Z1′(N′+K′)×K满秩。

使用置信传递解码的过程,实际上等价于对接收到的修复节点同正确接收到的源节点取消关联,因此置信传递解码过程之后的修复节点方程式R′=Z′N′×k×C′。同正确接收到的源节点不相关,即置信传递解码过程之后的修复节点等价于丢失节点异或而成。文献[5-6]中已经证明,当Z′N′×k满秩时,则一定可以通过高斯消元正确解码,即本设计方案可以正确解码。而同时,若Z′N′×k非满秩,则说明修复节点的度无法正确推导源节点,则其他所有方法也无法推导源节点。由此可证,本设计方案从理论上可以最大限度利用修复节点解码。

4.3 性能仿真比对

本次仿真的方法主要在应用层实现,软件实现使用C语言实现,运行在Linux 2.6操作系统内核,计算机中央处理器为Intel(R)Pentium(R)CPU@2.33 GHz。在实际测试中,本算例选择了节点大小为16 KB,节点个数K=1 024的数据块。

在编码过程中,分别选择了冗余为1%,2%,5%,10%的情况,其同传统速龙码编码时间消耗的测试数据对比结果如图5所示。结果表明,传统速龙码编码时间受冗余度影响较小,而快速速龙码编码时间几乎同冗余度呈正比;且快速速龙码在编码时间上较传统速龙码少很多,尤其是当冗余越小,差距越明显。

在解码过程,设置数据冗余率为20%,丢包率分别选取了1%,2%,5%,10%的情况。解码过程主要针对矩阵处理速度和完整解码速度进行对比。其最终的解码时间对比结果如图6所示。

图5 快速速龙码和传统速龙码编码耗时比对(K=1031)Fig.5 Encoding times compare in milliseconds between rapid raptor codes and raptor codes(K=1 031)

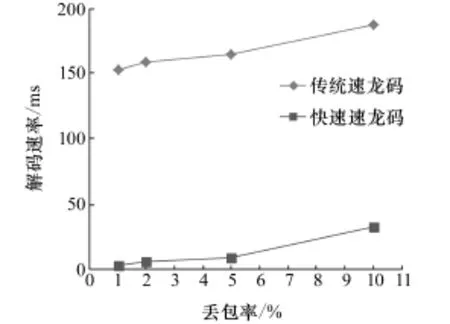
图6 快速速龙码和传统速龙码解码耗时比对(K=1031)Fig.6 Decoding times compare in milliseconds between rapid raptor codes and raptor codes(K=1 031)

针对不同的码长,设置数据冗余率为10%,丢包率都为5%,每个节点大小为16 kbit。码长K分别为250,500,1 000,1 500和2 000,其解码速度如图7所示。

从图6可以看到,由于矩阵本身的缩小,速龙码的矩阵规模大幅度下降,随着链路丢包率的降低,解码速度的提高越明显;如图7所示在相同丢包率(误码率)下,码长越长,快速速龙码解码速度提高越明显。与理论分析相符。

图7 不同码长下快速速龙码和传统速龙码解码耗时比对Fig.7 Decoding times compare in milliseconds in different source nodes K between rapid raptor codes and raptor codes

5 结束语

从上述结果可以看出,本设计方法的解码速度和编码速度较传统速龙码都有了极大的提高。本文基于速龙码编解码技术的基础上对其进行改进,提出快速速龙码,其主要特点和优势为:1)编码过程直接通过固定的生成矩阵计算修复节点,更加高效和简单;2)解码过程在进行高斯消元之前,先进行置信传递算法降度,大幅降低了解码矩阵的规模,从而大大减少了系统资源占用和时间复杂度。由于计算量和资源占用的减小,本文提出的快速速龙码更适用于航天器嵌入式软件环境下资源受限的情况。

[1] 张乃通,李晖,张钦宇.深空探测通信技术发展趋势及思考[J].宇航学报,2007,28(4):786-793.

ZHANG NAITONG,LI HUI,ZHANG QINYU.Thought and developing trend in deep space exploration and communication[J].Journal of Astronautics,2007,28(4):786-793.

[2] 顾术实,张钦宇,焦健.一种适用于深空通信的有限随机性喷泉码算法[J].宇航学报,2011,32(12): 2545-2549.

GU SHUSHI,ZHANG QINYU,JIAO JIAN.A novel algorithm of the limited-randomness fountaincodes in deep space communication[J].Journal of Astronautics,2011,32(12):2545-2549.

[3] MACKAY D J.Fountain codes[C]∥Proceedings of IEEE Communications,2005,152(6):1062-1068.

[4] LUBY M.LT codes[C]∥Procession of 43rd Annual IEEE Symptium Foundations of Computer Science, Vancouver,Canada,2002.

[5] SHOKROLLAHI A.Raptor codes[J].IEEE Transactions on Information Theory,2006,52(6):2551-2567.

[6] LUBY M,SHOKROLLAHI A,WATSON M.Raptor forward error correction scheme for object delivery[S]. www.ietf.org/rfc/rfc5053.txt,IETF,2007.

[7] 孙兆伟,刘源,邢雷,等.面向多任务的可重构星载计算机设计[J].系统工程与电子技术,2011,33(6): 1407-1414.

SUN ZHAOWEI,LIU YUAN,XING LEI,et al.Design of reconfigurable on-board computer for multitask[J]. Systems Engineering and Electronics,2011,33(6):1407-1414.

[8] ZHANG QUAN,XU WEIZHANG,SHI DONGXIN,et al.An improved algorithm of 3GPP MBMS raptor codes[C]∥2010 International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2010),2010.

[9] KIM S,LEE S,CHUNG S Y.An efficient algorithm for ML decoding of raptor codes over the binary erasure channel[J].IEEE Communications Letters,2008,12(8):578-580.

[10] 孟庆春,王晓京.Raptor Code预编码技术研究[J].计算机工程,2007,33(1):1-3.

MENG QINGCHUN,WANG XIAOJING.Research on precoding method in raptor code[J].Computer Engineering,2007,33(1):1-3.

An Efficient Encoding and Decoding Algorithm Suitable for Satellite Data Translation

ZHANG Yahang CHENG Bowen
(Beijing Institute of Spacecraft System Engineering,Beijing 100094)

A time-efficient fountain error-correcting codes called rapid raptor codes(RRC) was presented,which was better than the traditional raptor codes while maintaining the same symbol recoverable performance.Compared with the original raptor code,intermediate symbol and repair symbol generation were combined into one step in encoding process,and the conception of degrees of symbols from the belief-propagation(BP)decoder was imported in decoding process before Gaussian elimination decoding with a much smaller matrix size.The improved algorithm is much simple and has better time-efficient,therefore suitable for satellite application layer data translation,memory protection and deep space message translation.

Raptor Codes;Fountain Codes;Space translation;Satellite

10.3780/j.issn.1000-758X.2015.05.010

(编辑:王晓宇、范真真)

2014-12-19。收修改稿日期:2015-06-05

张亚航 1985年生,2010年获北京大学软件工程专业硕士学位,工程师。研究方向为星载软件设计、综合电子、空间信息安全。