基于混合遗传算法的电力系统源网协同调度

张杰，刘晓明，孙东磊，杨金洪，韩学山，钟振东

（1.国网山东省电力公司经济技术研究院，山东济南 250021；2.电网智能化调度与控制教育部重点实验室（山东大学），山东济南 250061；3.国网山东省电力公司临沂供电公司，山东临沂 276000）

电力系统经济调度的概念可追溯至20世纪20年代，电力系统中负荷的时空分布变化是经济调度问题产生的根本原因。实际上，调度主要是为应对负荷的变化，预先对机组出力进行优化决策，促使发电与负荷按预知轨迹平衡，其实质为固定电网结构下发电跟踪负荷的经济决策。经过近百年的发展，电力系统经济调度研究在理论和实践上已相对成熟[1-9]。

电力系统由源（指发电与负荷）和网（指输电设备）有机构成。随着电力市场竞争机制不断推进，电力负荷呈现多元化发展，风光等可再生能源发电以分布或集中形式大规模地并入电网，电力系统中源网间呈现日趋交织纠结的矛盾[10-11]，电网构架出现与其不相适应的非同调现象，即输电阻塞问题，该问题仅靠改变发电方式已难以抑制。为有效缓解这一矛盾，出现了改变电网元件状态（电网络重构）来解决这一问题的研究，提出考虑电网拓扑控制的安全校正方法[12-13]，以及融入电网拓扑优化的调度方法[14-16]。

为保证电网可靠运行同时兼顾电力供求增长等因素，实际规划的电网拓扑架构及其传输容量均处于冗余状态，但电网实际运行中并不是冗余度越高，系统越可靠，这就是电力系统可靠性问题的非同调现象[17]，即一个元件从系统中缺省反而产生一个更可靠的系统状态。新形势下电力系统中被动的源（负荷以及可再生能源发电等）呈现复杂多变的情形，固定电网结构将使经济调度中源网间关系更多地处于冲突状态[18]。实际上，经济调度中源网间的矛盾主要是由于电网络的基尔霍夫电压定律约束制约了部分输电元件传输容量的发挥，使得经济发电机组发电外送能力受到限制，严重时威胁源平衡的实现，即对应调度无可行解的情况。因此，调度决策中有选择地对电网输电线路状态进行调整不仅有助于源平衡的实现，而且对提高系统运行的经济性具有重要作用。电网拓扑优化已在改善系统可靠性方面得到应用[19-20]。然而，单纯地为实现发电负荷平衡在决策的电网拓扑调整则可能会影响系统的可靠性，如造成系统解列等[21]。虽然源网协同调度决策的系统解列各子系统内会实现功率平衡，而且现代电力系统具备了主动解列的能力，但是过于频繁的系统解列和同步在实际系统运行中是不允许的，因为其实现具有较大的难度，尤其是对大系统而言，则可能会出现影响系统安全运行的连锁反应。因此，如何保证拓扑连通性是源网协同调度要考虑的主要因素。该约束的引入打破了传统经济调度模型的纯数学解析模型形式，由此，给出保证系统拓扑连通性的源网协同调度模型及其求解是本文研究的宗旨。

本文提出了一种源网协同调度模型，其在经济调度原有条件的基础上，将电网输电支路状态纳入决策量，并计及电网拓扑连通性条件，以在满足系统运行约束条件的基础上挖掘系统实现发电负荷平衡的协同能力。针对该模型，给出了遗传算法和线性规划内点法混合求解方法。最后，通过算例分析对本文方法进行了有效性验证。

1 电力系统源网协同调度模型

电力系统源网协同调度模型是在直流潮流的条件下以追求发电成本最小为目标，同时满足系统运行的物理和技术约束条件，以对常规发电机组有功功率、电网输电元件状态进行预先安排。为便于表述，本文中统一以上标“max”和“min”分别表示相应变量的上下限。

1.1 目标函数

式（1）中：NG为常规发电机组集合；cg为机组g发电成本。

1.2 约束条件

1）常规发电机组发电成本约束

式（2）中：Pg为机组g有功功率；ag1、bg1、ag2和bg2

为机组g发电成本函数分段线性成本系数。

2）常规发电机组有功范围约束

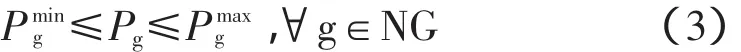
3）电网安全范围约束

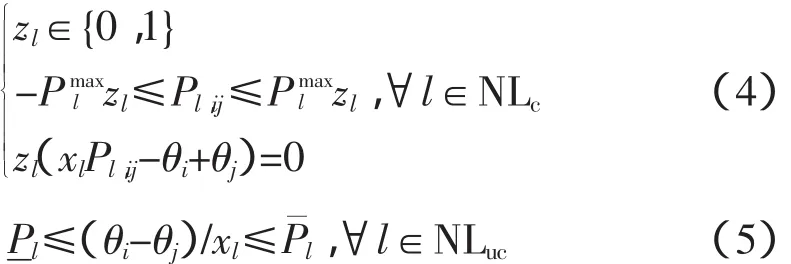
式中：zl和xl分别为输电支路l的运行状态和电抗；zl=1为支路在线运行；zl=0为支路停运；Pl，ij为支路l有功功率，其首、末端节点分别为节点i、j，θi和θj分别为其电压相角；NLc和NLuc分别为可控、不可控电网支路集合。

4）节点功率平衡约束

式（6）中：NB为节点集合；NG（i）和ND（i）分别为节点i上的常规发电机组和负荷集合；NSc（i）、NEc（i）、NSuc（i）和NEuc（i）分别为以节点i为首、末端节点的可控、不可控输电支路集合。需说明的是，风电等不可调度的可再生能源发电功率当作“负的负荷”，因此，将可再生能源发电归入负荷集合。

5）电压相角范围约束

式（7）为提高计算效率而添加的电压相角范围约束，因为实际上参考电压相角为0时，系统电压相角通常在[－π，π]范围内，由此引入式（7）可一定程度上缩小问题寻优范围，从而提高计算效率。

6）拓扑连通性约束

式（8）中：α为系统开断支路个数；Hα×α为系统开断α条支路后的α×α阶系统连通性判别阵，关于系统连通性判别阵将在2.2节详细说明；rank（·）为求取矩阵的秩。因此，式（8）为系统拓扑连通性条件为开断α条支路后α×α阶系统连通性判别阵为满秩矩阵，即矩阵Hα×α非奇异。

7）支路开断数量约束

式（9）中：αmax为由于调控系统控制能力等限制的最大允许开断支路数，假设各支路初始状态均在线运行。

8）参考节点电压相角约束

式（10）中：n为电压参考节点的节点号。

2 模型求解方法

拓扑连通性约束的引入打破了传统经济调度模型的纯数学解析模型形式，基于此，本文所提模型由遗传算法[22]与线性规划原对偶路径跟踪内点法[23]组合求解。即由遗传操作获得满足拓扑连通的个体，并由给定电网结构下的安全经济调度进行个体适应度评价，其中安全经济调度由线性规划原对偶路径跟踪内点法组合求解。

2.1 遗传算法编码格式

遗传操作过程中仅对输电支路状态编码。若将每一输电支路状态均对应到染色体的基因位，将会显著增加遗传操作的复杂度和计算量，对此，本文采用一种新的编码方式，即对选取的待决策的支路编号及其运行状态变量分别记录的编码方式，具体编码格式可表示为：

采用式（11）所示方式对输电支路状态变量进行编码，使得所得到的个体自动满足最大允许支路开断数量的要求。

2.2 网络拓扑连通性判别

由于系统允许的支路同时开断数量有限，为精简计算量，基于图论中最小割集的概念以判断系统拓扑连通性，若系统开断α条支路，开断支路集合NL（α），只需对α×α阶系统连通性判别阵Hα×α的奇异性进行判别，若Hα×α奇异，则系统解列，否则连通。关于系统连通性判别阵Hα×α的具体说明如下。

在直流潮流条件下，支路传输有功功率与各节点注入功率之间满足线性关系，即

式（12）中：PI和PL分别为节点注入有功功率、支路传输有功功率向量；n为系统节点个数；nl为系统支路个数；Ψ为注入转移因子矩阵[24]，其表征了支路传输有功功率与节点注入功率的灵敏度信息，Ψ=BLA（ATBLA）-1，其中BL为支路电纳对角矩阵；A为节点支路关联矩阵。由此可以推知，若考虑任一支路两端节点电量交易，则系统各支路传输功率的响应特性可表示为：

式（13）中：Φ为功率传输分布因子矩阵[25]，其元素φl，m表征了支路l传输有功功率与支路m两端节点电量交易的灵敏度信息。若|φl，l|=1，则显然支路l为系统的最小割集。由此可以归纳推知，当n条支路开断后，该开断支路集合NL（n）为系统最小割集的条件为：

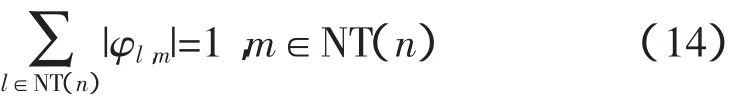
当系统开断α条支路时，系统解列的条件就是开断支路集合NL（α）包含至少一个最小割集。由文献[24]可知，其等价条件即为α×α阶矩阵Hα奇异，其中矩阵Hα为

式（15）中：矩阵Iα为α×α阶单位阵，ΦNL（α）为由开断支路集合NL（α）构成的功率传输分布因子子阵。为便于表述，本文将矩阵Hα称为系统连通性判别阵。

网络拓扑连通性判别的具体流程为：1）形成各支路均在线情况下的系统功率传输分布因子矩阵Φn×n；2）由遗传操作获得的开断支路集合NL（α），形成对应的功率传输分布因子子阵ΦNT（α）；3）对任意支路l、m∈NL（α）判别|φl，l|是否为1，若是则结束；否则判断∑m∈NL（α）|φl，m|是否为1，若是则结束；否则形成系统连通性判别阵Hα×α，判断其行列式是否为0，若是则不连通，否则连通。

2.3 线性规划内点法求解

拓扑状态确定后的模型即为传统形式的安全经济调度模型，其本质为直流最优潮流，由初始点不可行的多项式时间求解时间的原-对偶路径跟踪内点法[23]求解。

2.4 求解流程

本文模型求解的具体流程如图1所示。

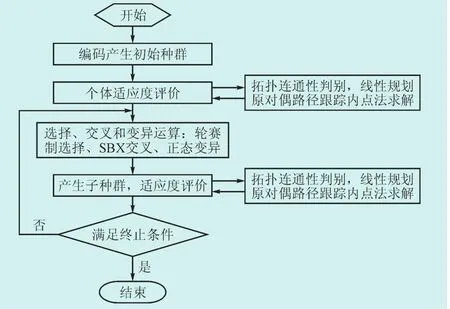
图1 模型求解流程图Fig.1 Solution flow chart of the model proposed

3 算例分析

算例仿真在主频为3.1 GHz、内存为16 GB的计算机上实现，在Microsoft visual studio 2008环境下，采用C++语言编制本文求解源网协同调度问题的混合遗传算法程序。遗传算法参数设置如下：种群规模为40，最大迭代次数为20，交叉率为0.9，变异率为0.1。

3.1 算例1

算例1分析基于图2所示的某实际电力系统。表1至表4分别给出了该系统电网元件参数、常规发电机组参数、负荷数据以及风电数据。若在固定电网构架下，实施安全经济调度，经计算无可行解，究其原因为线路13-14传输容量限制导致了同一回路中的输电线路7-6、7-2的输电能力不能充分发挥，造成功率传输瓶颈，而节点2和节点4上发电机出力达到上限，由此，切负荷情况在所难免。对此，以本文源网协同调度模型进行求解，得到最大允许开断支路数不超过3时最优的开断支路集合如表5所示。

图2 实际系统等值接线图Fig.2 A wiring graph of an actual power system

表1 实际系统电网元件参数Tab.1 Branch parameters for the actual power system

表2 实际系统机组参数Tab.2 Generator parameters for the actual power system

由表5可知，开断支路14-15后，功率传输瓶颈打开，由此可得到可行的经济调度解，此时常规发电机组的最优运行方式如表6所示。

表3 实际系统负荷数据Tab.3 Load data of the actual power system

表4 实际系统风电数据Tab.4 Wind power data of the actual power system

表5 实际系统最优停运支路集合Tab.5 Optimal branch-outage sets of the actual power system

表6 常规发电机组最优运行方式Tab.6 Optimal operation pattern for generators

由表6可知，开断支路14-15后，功率传输瓶颈打开，而节点2机组边际成本低于节点4上机组边际成本，但受制于支路2-3达到功率上限，节点2机组出力受限。而在此基础上，开断支路3-4单回线，则可从电网传输角度缓解该现象，发电成本因此也会相应减少，此时常规发电机组的最优运行方式如表7所示。

3.2 算例2

以含风电的IEEE 118节点系统为例，风电场位置以及风功率数据见表8，IEEE 118节点系统由118母线，19台发电机，99个负荷以及186条输电支路组成，具体数据参见文献[20]。以本文源网协同调度模型进行求解，得到最大允许开断支路数不超过5时最优的调度结果如表9所示。

表7 常规发电机组最优运行方式Tab.7 Optimal operation pattern for generators

表8 含风电的IEEE 118节点系统风电场数据Tab.8 Wind farm data for the IEEE 118-bus system with wind power integration

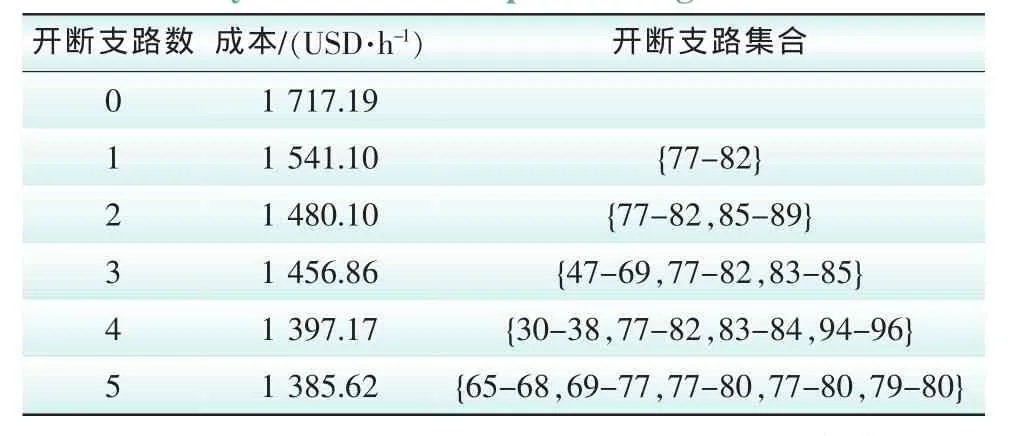
表9 含风电的IEEE 118节点系统调度结果Tab.9 Optimal dispatch results for the IEEE 118-bus system with wind power integration

表9中开断支路数为0即对应传统的安全经济调度情况。从表9可以看出，随着开断支路数的增加，系统发电成本降低，其主要原因为部分经济发电机组发电外送能力得到释放。

4 结论

新形势下源网间呈现日趋交织纠结的矛盾，对此，本文提出一种电力系统源网协同调度模型，模型中将电网输电支路状态纳入调度决策，能够扩大调度决策解的空间，提高电力系统发电负荷平衡能力以及电网运行的经济性；针对源网协同模型求解困难的情况，本文提出求解源网协同调度问题的遗传算法和线性规划原对偶路径跟踪法组合求解方法，算例分析表明该方法的有效性，对最大化系统源平衡能力和电网运行经济性具有重要意义。

本研究是电力系统协同调度的重要组成部分。进一步会将这一方法拓展到考虑预想事故的安全校正的源网协同调度优化之中，以满足实际系统应用需求，预期会促进新形势下电网调度理论的进展。此外，如何保证系统满足一定的可靠性指标以满足实际系统应用需求仍需要下一步的深入研究。

[1]WOOD A J，WOLLENBERG B F．Power generation，operation，and control[M]．北京:清华大学出版社，2003.

[2]CARPENTIER J.Contribution a l’etude du dispatching economique[J].Bulletin de la Societe Francaise des Electriciens，1962，3（8）:431-447．

[3]XU G，GALIANA F D，LOW S.Decoupled economic dispatch using the participation factors load flow[J].IEEE Trans on Power Apparatus and Systems，1985，PAS-104（6）:1377-1384.

[4]韩学山．动态优化调度的积留量法[D]．哈尔滨：哈尔滨工业大学，1994．

[5]张伯明，吴文传，郑太一．消纳大规模风电的多时间尺度协调的有功调度系统设计[J]．电力系统自动化，2011，35（1）：1-6.ZHANG Boming，WU Wenchuan，ZHENG Taiyi.Design of a multi-time scale coordinated active power dispatching system for accommodating large scale wind power penetration[J].Automation of Electric Power Systems，2011，35（1）:1-6（in Chinese）.

[6]王林，杨佳俊，陈红，等.含风电场的电网潮流计算[J].电力电容器与无功补偿，2015（1）:49-53.WANG Lin，YANG Jiajun，CHEN Hong，et al.Power flow calculation of wind power integrated systems[J].Power Capacitor ＆ Reactive Power Compensation，2015（1）:49-53（in Chinese）.

[7]钟世民，韩学山，刘道伟．计及校正控制的安全约束最优潮流的奔德斯分解算法[J].中国电机工程学报，2011，31（1）：65-71．ZHONG Shimin，HAN Xueshan，LIU Daowei.Benders decomposition algorithm for corrective security-constrained optimal power flow[J].Proceedings of the CSEE，2011，31（1）:65-71（in Chinese）.

[8]郭三刚，张琳，翟桥柱，等.具有安全约束的发电机组组合可行的充分必要条件[J].热力发电，2011（3）:39-45．GUO Sangang，ZHANG Lin，ZHAI Qiaozhu，et al.A necessary and sufficient condition for determining the feasibility of generating units combination with security constraint[J].Thermal Power Generation，2011（3）:39-45（in Chinese）.

[9]赖菲，王智微，杨东，等.利用启发式方法求解带有爬升约束的火电机组多时段经济调度[J].热力发电，2013（5）:15-18．LAI Fei，WANG Zhiwei，YANG Dong，et al.A new heuristic approach for unit commitment[J].Thermal Power Generation，2013（5）:15-18（in Chinese）.

[10]王鹏，任冲，彭明侨.西北电网风电调度运行管理研究[J].电网与清洁能源，2009，25（11）:80-84．WANG Peng，REN Chong，PENG Mingqiao.A study on wind power dispatching operation and management in northwest power grid[J].Power System and Clean Energy，2009，25（11）:80-84（in Chinese）.

[11]衣立东.电网与可再生能源协调发展研究[J].电网与清洁能源，2008，24（1）:6-9．YI Lidong.Harmonizing development between power system and renewable energy[J].Power System and Clean Energy，2008，24（1）:6-9（in Chinese）.

[12]LI M，LUH P B，MICHEL L D.Corrective line switching with security constraints for the base and contingency cases[J].IEEE Trans on Power Systems，2012，27（1）:125-133.

[13]GOU B，ZHANG H.Fast real-time corrective control strategy for overload relief in bulk power systems[J].IET Generation，Transmission&Distribution，2013，7（12）:1508-1515.

[14]O′NEILL R P，BALDICK R，HELMAN U.Dispatchable transmission in RTO markets[J].IEEE Trans on Power Systems，2005，20（1）:171-179.

[15]FISHER E B，O′NEILL R P，FERRIS M C.Optimal transmission switching[J].IEEE Trans on Power Systems，2008，23（3）:1346-1355.

[16]HEDMAN K W，FERRIS M C，O′NEILL R P，et al.Cooptimization of generation unit commitment and transmission switching with N-1 reliability[J].IEEE Trans on Power Systems，2010，25（2）:1052-1063.

[17]李文沅，周家启，谢开贵，等．在输电线和变电站组合联结网络中的非同调现象[J]．中国电机工程学报，2006，26（14）：7-11．LI Wenyuan，ZHOU Jiaqi，XIE Kaigui.Non-coherence phenomenon in combinative transmission line and substation configurations[J].Proceedings of the CSEE，2006，26（14）:7-11（in Chinese）.

[18]刘国静，韩学山，杨明，等．经济调度中源网间的三种状态分析及验证[J]．电网技术，2013，37（2）：431-437．LIU Guojing，HAN Xueshan，YANG Ming，et al.Analysis and verification on three states between source and network in economic dispatch[J].Power System Technology，2013，37（2）:431-437（in Chinese）.

[19]SCHNYDER G，GLAVITSCH H.Security enhancement using an optimal switching power flow[J].IEEE Trans on Power Systems，1990，5（2）:674-681.

[20]ROLIM J G，MACHADO L J B.A study of the use of corrective switching in transmission systems[J].IEEE Trans on Power Systems，1999，14（1）:336-341.

[21]KHODAEI A，SHAHIDEHPOUR M.Transmission switching in security-constrained unit commitment[J].IEEE Trans on Power Systems，2010，25（4）:1937-1944.

[22]熊信银，吴耀武.遗传算法及其在电力系统中的应用[M].武汉：华中科技大学出版社，2002.

[23]VARGAS L S，QUINTANA V H，VANNELLI A.A tutorial description of an interior point method and its applications to security-constrained economic dispatch[J].IEEE Trans on Power Systems，1993，8（3）:1315-1324.

[24]LIU M，GROSS G.Role of distribution factors in congestion revenue rights applications[J].IEEE Trans on Power Systems，2004，19（2）:802-810.

[25]GÜLER T，GROSS G.Detection of island formation and identification of causal factors under multiple line outages[J].IEEE Trans on Power Systems，2007，22（2）:505-513.