含分数阶导数项的随机Duffing振子的稳态响应分析

孙春艳, 徐 伟

(1．山东大学(威海)数学与统计学院，山东 威海 264209； 2.西北工业大学应用数学系，陕西 西安 710072)

含分数阶导数项的随机Duffing振子的稳态响应分析

孙春艳1, 徐 伟2

(1．山东大学(威海)数学与统计学院，山东 威海 264209； 2.西北工业大学应用数学系，陕西 西安 710072)

对一个含有分数阶导数项阻尼的、Gaussian白噪声激励下的Duffing振子进行了稳态响应分析。首先，基于能量平衡理论，运用等效线性化方法，计算等效系统的线性阻尼及自然频率，建立统计意义下的等效线性化系统。然后，利用平均法建立随机It方程，得到随机响应的Markovian近似；给出描述振子振幅概率密度函数演化的Fokker-Planck方程，并得到它的稳态解。进一步，对于含有响应振幅的等效线性系统，借助由Laplace变换得到的转换函数，得到原系统的条件功率谱密度，结合振幅的稳态概率密度作为权重函数，给出原系统功率谱密度的估计，以及响应的统计量的估计。数值模拟的结果说明所提出的功率谱密度的近似解析表达式是可靠的，它甚至适用于Duffing振子具有强非线性回复力的情形，因为它可以较好地表现出功率谱密度共振频谱加宽及多峰现象的出现。

分数阶导数； 等效线性化法； 随机平均法； 条件功率谱密度； 响应的功率谱密度估计

引 言

随机响应分析是随机动力学研究的重要方面，已有了一些经典的方法和结果[1-3]。对于响应的功率谱密度，文献[4]利用经典的等效线性化方法表现出缺陷，它给出的估计得到了正确的共振频率，却高估了共振处的峰值而且低估了频谱的宽度。一种改进的等效线性化方法在文献[5]中被提出，它与传统方法的主要区别在于将等效线性系统的待定参数设定为响应振幅的函数，从而建立了一个求解等效的线性刚度的计算方法。在文献[6]中，首次出现了术语“条件功率谱密度”，并通过与随机平均法的结合，以概率密度函数为权重函数，将响应的功率谱密度作为条件功率谱密度的加权和，给出了随机响应功率谱密度的有效估计。在文献[4]中被正式提出后，条件功率谱密度的概念开始被广泛地应用于响应功率谱密度的估计，给出了理想的近似解析结果，但它的数学严密性及合理性的说明却一直是一个空白，直到在文献[7]中，Spanos等才给出了严格的证明。

近年来，分数阶微积分在结构动力学及工程力学领域，越来越多的研究表明分数阶导数可以用较少的参数来模拟某些黏弹性材料的本构关系[8-10]，在确定性的响应分析中，基于特征向量展开，Laplace变换[8-9]和Fourier变换[11]被用来得到精确的解析解。文献[12]中，平均法被用来分析响应的振幅。在随机响应的情形，已有的方法主要适用于求解弱非线性系统。文献[13]中，基于广义谐和函数的随机平均法被用于对高斯白噪声激励下的含有分数阶导数的强非线性系统进行随机响应分析。此外，数值方法方面，已有的结果如有限差分方法、有限元方法及无网格方法等[14-16]，都一定程度上受到分数阶导数全局依赖性这一本质特征对计算速度的影响。文献[17]给出的算法在一定程度上减低了分数阶导数项对历史数据的依赖和记忆性，提高了数值计算的速度。

本文旨在建立一个对含有分数阶导数项的随机Duffing振子进行随机响应分析的方法。利用改进的等效线性化方法，首先得到一个含分数阶导数项的线性系统，其中的线性阻尼及自然频率都是振幅的函数。将分数阶导数项作为一个弱阻尼项，对得到的系统运用平均法，建立随机It方程，得到响应的Fokker-Planck方程并求得其稳态解。然后，借助Laplace变换，得到等效线性系统的转换函数及条件功率谱密度，并综合之前的结果，对条件功率谱密度利用振幅的概率密度函数进行加权求和，得到原系统响应功率谱密度的估计。最后，通过数值模拟的结果来验证响应的稳态概率密度及功率谱密度轨迹的合理性。

1 含分数阶导数项的随机Duffing振子

考虑一个高斯白噪声激励下的含分数阶导数项的Duffing振子

(1)

(2)

(3)

(4)

并引入参数D=πS0来表征噪声的强度。

2 等效线性化系统

有别于传统的等效线性化方法，从能量平衡的角度，改进的线性化方法认为原振动结构的能耗与等价系统的能耗相同，以此得到等价线性系统的待定阻尼系数，而待定的自然频率可以通过完全独立的其他方法来得到，普遍的方法是将它认为是原系统的共振频率[19]。

将待定的阻尼及刚度系数作为系统振幅响应的函数，设等价线性振动结构为

(5)

(6)

利用广义谐波平衡技术，可以得到如下的待定系数，使误差(6)达到均方意义的最小

(7)

至此，可以得到等效的线性系统为

(8)

3 平均法、随机响应的稳态概率密度

在弱阻尼下随机系统的响应分析中，平均法可以建立原系统振幅响应的Markovian近似，并通过求解描述振幅概率密度函数演化的Fokker-Planck方程，得到随机响应的概率分布及统计特性。对于线性系统(8)，当阻尼系数ξ是一个小量时，它在原点附近的运动可以被看作是周期的，据此引入变换

(9)

(10)

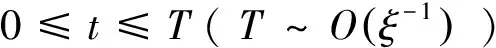
(11)

这里m(A)和σ(A)分别为待定的漂移和扩散系数，B(t)是单位Wiener过程。

(12)

为计算m(A)，需要分别计算两个确定性平均，对0<α<1，其中第一项有

(13)

其中

(14a)

(14b)

由于A(t)和Θ(t)都是慢变变量，式(14)中

(15)

即有

(16)

对于式(16)中的Fresnel积分，引入渐近积分

(17a)

(17b)

将式(16)及(17)代入L1和L2，得到

(18)

及

(19)

综上，当0<α<1时，平均后的结果为

(20)

对于1<α<2的情形，类似的推导得到

(21)

将式(20)及(21)代入计算公式(12)，结合G1和G2的表达式，得到漂移系数

m(A)=

(22)

及扩散系数

(23)

对于It随机微分方程(11)，描述随机响应的概率密度函数变化的Fokker-Planck方程为

(24)

在稳态情形，方程(24)的解为

(25)

式中C为归一化常数。

图1～4给出了振幅响应的稳态概率密度，通过不同阶数α及不同非线性程度ε下近似解析结果与数值模拟结果的对比，说明式(25)给出的结果的合理性。其中数值模拟采用的参数分别为：D=0.1，ξ=0.1，ω0=2，其他参数取值不同，分别在图中给予说明。从图1和2中可以看出，当分数阶阶数α取值为0.5时，对于强非线性系统情形，即ε=1及ε=3，利用随机平均法所得到的稳态概率密度函数与响应的数值模拟结果十分贴近。这说明，在0<α<1时，所得到的稳态概率密度的近似解析结果是有效的。类似地，图3和4给出了分数阶阶数α取值为1.5时稳态概率密度解析解与模拟解的对比情况，对ε=1及ε=3两种情形，近似解析解与数值模拟解很好的吻合，说明所得到的解析解在1<α<2时也是有效的。

图1 α=0.5，ε=1时振幅的稳态概率密度Fig.1 The stationary probability density function for α=0.5, ε=1

图2 α=0.5，ε=3时振幅的稳态概率密度Fig.2 The stationary probability density function for α=0.5, ε=3

图3 α=1.5，ε=1时振幅的稳态概率密度Fig.3 The stationary probability density function for α=1.5，ε=1

图4 α=1.5，ε=3时振幅的稳态概率密度Fig.4 The stationary probability density function for α=1.5，ε=3

4 功率谱密度估计

对于得到的等效线性系统(8)，在系统达到稳态时，任意给定一个振幅的观测值A=a，即可得到一个等效系统

(26)

与系统(26)对应的转换函数为

(27)

由此可以得到系统(26)响应的功率谱密度

(28)

(29)

随即可以得到响应的统计特征，如原系统稳态位移响应的方差为

(30)

5 数值结果

为了验证式(29)给出的响应的功率谱密度估计，将近似的解析结果与数值模拟的结果进行对比。图5～8中，参数分别为：D=0.1，ξ=0.01，ω0=2，Welch法被运用于响应的数值模拟结果，得到响应功率谱密度的Welch法估计。观察图5及6，在分数阶阶数α取值为0.5时，对于ε=1及ε=3，对比式(29)给出的近似解析结果与数值结果，响应的功率谱密度的估计不仅给出了正确的共振位置，也给出了合理的共振频谱带宽。说明在0<α<1时，利用条件功率谱密度所建立的式(29)给出的响应的功率谱密度估计是有效的。同样地，对比图7及8，在分数阶阶数α取值为1.5时，对于ε=1及ε=3的情形，对比式(29)给出的近似解析结果与数值结果，响应的功率谱密度的估计都给出了正确的共振位置及合理的共振频谱带宽，并有效地表现共振出频谱加宽及多峰现象的出现。说明在1<α<2时，利用条件功率谱密度所建立的式(29)给出的响应的功率谱密度估计是有效的。为进一步说明响应功率谱密度估计的有效性，利用式(30)所得到的位移响应方差的近似解析结果与模拟结果进行对比，得到图9，说明所得到的响应的功率谱密度估计可以很好地用于计算响应的统计特性。

图5 α=0.5，ε=1时响应的功率谱密度估计Fig.5 Response power spectral density estimation for α=0.5, ε=1

图6 α=0.5，ε=3时响应的功率谱密度估计Fig.6 Response power spectral density estimation for α=0.5, ε=3

图7 α=1.5，ε=1时响应的功率谱密度估计Fig.7 Response power spectral density estimation for α=1.5, ε=1

图8 α=1.5，ε=3时响应的功率谱密度估计Fig.8 Response power spectral density estimation for α=1.5, ε=3

图9 位移响应的方差Fig.9 Variance for the displacement response

6 结 论

对于含分数阶导数项的强非线性随机Duffing振子，本文给出了一个响应功率谱密度估计的程序。在假设分数阶导数项表现为结构阻尼的前提下，本文给出的功率谱密度估计程序是可靠的，即使是在较强的非线性系统情形。首先，利用改进的等效线性化法，得到一个与原系统等效的含分数阶导数项的线性随机Duffing振子，通过计算等价系统的线性阻尼和自然频率，原系统的非线性回复力被一个线性的回复力代替，而且它是振幅响应的函数。然后，随机平均法被作用于得到的线性振子，通过系统振幅响应的Markovian近似，建立了振幅响应的随机It方程；写出描述振幅概率密度函数演化的Fokker-Planck方程，并给出其稳态解。最后，利用等效线性系统的转换函数，得到随机响应的条件功率谱密度，并结合得到的振幅稳态概率密度函数，得到响应功率谱密度的估计。数值结果表明，文中所给出的近似解析结果，无论是振幅的稳态概率密度还是响应的功率谱密度，对于包括强非线性回复力情形在内的稳态响应分析都是有效的，尤其对于强非线性系统，所给出的估计可以表现出响应功率谱密度频谱的加宽及高次谐波的出现。这在一定程度上说明“改进的”等效线性化方法是可靠的，并且，将分数阶导数项作为一个弱阻尼项的假设是合理的，且基于此建立的随机平均法是适用的；条件功率谱密度在含分数阶导数项的系统中仍然适用，说明了它是一个对随机响应进行功率谱密度估计的有效工具。

[1] Robert J B, Spanos P D. Stochastic averaging: an approximate method of solving random vibration problems[J]. International Journal of Non-linear Mechanics, 1986, 21(2): 111—134.

[2] Robert J B, Spanos P D. Random Vibration and Statistical Linearization[M]. New York: Dover Publications, 2003.

[3] Zhu W Q. Recent developments and applications of the stochastic averaging method in random vibration[J]. Applied Mechanics Reviews, 1996, 49(10S): S72.

[4] Bouc R. The power spectral density of response for a strongly non-linear random oscillator[J]. Journal of Sound and Vibration, 1994, 175(3): 317—331.

[5] Miles R N. An approximate solution for the spectral response of Duffing′s oscillator with random input[J]. Journal of Sound and Vibration, 1989, 132(1): 43—49.

[6] Miles R N. Spectral response of a bilinear oscillator[J]. Journal of Sound and Vibration， 1993, 163(2): 319—326.

[7] Spanos P D, Kougioumtzoglou I A, Soize C. On the determination of the power spectrum of randomly excited oscillators via stochastic averaging: An alternative perspective[J]. Probabilistic Engineering Mechanics, 2011, 26(1): 10—15.

[8] Bagley R L, Torvik P J. Fractional calculus-a different approach to the analysis of viscoelastically damped structures[J]. AIAA Journal, 1983, 21(5): 741—748.

[9] Bagley R L, Torvik P J. Fractional calculus in the transient analysis of viscoelastically damped structures[J]. AIAA Journal, 1985, 23(6): 918—925.

[10]Koeller R C. Application of fractional calculus to the theory of viscoelasticity[J]. ASME Journal of Applied Mechanics, 1984, 51(2): 299—307.

[11]Gaul L, Klein P, Kemple S. Impulse response function of an oscillator with fractional derivative in damping description[J]. Mechanics Research Communications, 1989, 16(5): 297—305.

[12]Wahi P, Chatterjee A. Averaging for oscillations with light fractional order damping[A]. Proceedings of ASME 2003 Design Engineering Technical Conferences and Computers and Information in Engineering Conference[C]． Chicago, 2003: 721—727.

[13]Huang Z L, Jin X L. Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative[J]. Journal of Sound and Vibration, 2009, 319(3-5): 1 121—1 135.

[14]Diethelm K, Ford N J, Freed A D et al. Algorithms for the fractional calculus: A selection of numerical methods[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(6-8): 743—773.

[15]Diethelm K, Ford N J, Freed A D. A predictor-corrector approach for the numerical solution of fractional differential equations[J]. Nonlinear Dynamics, 2002, 29(1-4): 3—22.

[16]Yuan L, Agrawal O P. A numerical scheme for dynamic system containing fractional derivatives[J]. Journal of Vibration and Acoustics, 2002, 124(2): 321—324.

[17]Spanos P D, Evangelatos G I. Response of a non-linear system with restoring forces governed by fractional derivatives-time domain simulation and statistical linearization solution[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(9): 811—821.

[18]Podlubny I. Fractional Differential Equations[M]. London: Academic Press, 1999.

[19]Goto H, Iemura H. Linearization techniques for earthquake response of simple hysteretic structures[J]. Proceedings of the Japaneese Society of Civil Engineering, 1973, 212:109—119.

Stationary response analysis for a stochastic Duffing oscillator comprising fractional derivative element

SUNChun-yan1,XUWei2

(1．School of Mathematics and Statistics, Shandong University, Weihai 264209, China;2．Department of Applied Mathematics, Northwestern Polytechnical University, Xi′an 710072, China)

Stationary response is investigated for a Duffing oscillator comprising fractional derivative elements excited by Gaussian white noise in the present paper. Firstly, harmonic balance technique is adopted to form a statistically equivalent linear system. Then, stochastic averaging is applied to the system to obtain a Markovian approximation of the response amplitude, and the associated Fokker-Planck equation and its stationary solution are derived. Furthermore, in virtue of Laplace transform, the transfer function of the equivalent linear system with amplitude-dependent coefficients is derived and it gives the conditional power spectral density, after weighted by the stationary probability density function, estimations of the power spectral density for the response and related statistics are derived. Numerical simulations verify the reliability of the proposed procedure, even for strongly nonlinear oscillators with properties like spectrum broadening and multimodal pattern.

fractional derivative; equivalent linearization; stochastic averaging; conditional power spectral density; response power spectral density estimation

2014-03-26；

2014-09-01

国家自然科学基金资助项目(11772233)

O322； O324

A

1004-4523(2015)03-0374-07

10.16385/j.cnki.issn.1004-4523.2015.03.006

孙春艳(1984—)，女，博士。电话：13679122401；E-mail: sunchunyan@mail.nwpu.edu.cn