基于Conwep方法的钢筋混凝土板毁伤研究

羊 勇，常春伟，管 晔，李北杰，常 健

(1.军事交通学院研究生管理大队，天津300161;2.军事交通学院 国防交通系，天津300161;3.军事交通学院学员旅，天津300161)

突发性爆炸事件常导致重大经济损失和人员伤亡，建筑物受爆炸作用往往会造成局部破坏、结构损伤甚至整体连续倒塌，造成更大范围的人员伤亡［1］。2015年天津8·12特大爆炸事故中，爆炸中心区的建筑物在爆炸作用下毁伤严重，爆炸周边区域的人员伤亡巨大。现代战争条件下，随着精确制导武器的大规模应用，交通重点目标的暴露和被毁概率大大增加，交通网络受精确制导武器打击的威胁越来越大，对建筑物的抗爆性展开研究非常必要。

现代建筑物以钢筋混凝土结构为主，为了提高建筑物抗爆安全性和战场生存能力，有效降低爆炸造成的危害和损失，必须对爆炸作用下钢筋混凝土结构的毁伤机理进行研究。其中钢筋混凝土板件是现代钢筋混凝土建筑物的基本组成构件。因此，本文对爆炸荷载作用下钢筋混凝土板毁伤效应进行研究，为下一步研究爆炸作用下大型建筑物毁伤机理提供基础性支持，为交通重点目标平时建设中的抗爆设计和战时受打击后的毁伤评估提供相应技术支持。

本文利用显式动力分析有限元软件Ansys/LS-DYNA，使用Conwep方法计算和加载爆炸荷载，选用MAT_CONCRETE_DAMAGE_REL3(MAT_072R3)混凝土材料模型，对汪维［2］71所做的爆炸载荷作用下钢筋混凝土板毁伤试验进行有限元数值仿真，对仿真结果和试验数据进行对比分析，以验证本文数值仿真方法的有效性和可靠性，并对爆炸荷载作用下钢筋混凝土板的破坏模式进行研究，为下一步大型建筑物爆炸毁伤研究提供可靠的仿真方法。

1 钢筋混凝土板爆炸试验

2012 年，汪维［2］37-42为研究爆炸载荷作用下钢筋混凝土构件和结构的动力响应及破坏模式，对钢筋混凝土板和梁进行了一系列的爆炸试验。本文选取该研究中的编号P 2-3钢筋混凝土板爆炸试验进行数值仿真研究。该板试件尺寸为110 cm×100 cm×4 cm，配筋方式为双向单层，横向和纵向配筋均为Φ6 HPB2 3 5，配筋间距为7.5 cm，配筋分布如图1所示。设计混凝土强度40 MPa，对应轴心抗压强度 26.8 MPa［3］。钢筋直径6 mm，试验测得屈服强度为395 MPa。试验TNT当量460 g，爆炸点位于板正中心上方，距离迎爆面40 cm，比例距离为0.518 m/kg1/3。

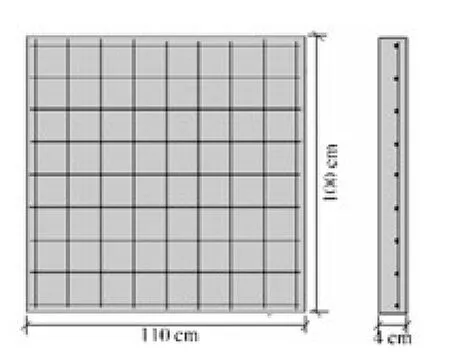
图1 板试件尺寸及配筋分布

2 数值仿真模型

2.1 有限元模型

编号P 2-3钢筋混凝土板爆炸试验中，钢筋混凝土板两端固支，起爆点位于迎爆面中心的正上方，结构具有对称性，建立1/4钢筋混凝土板有限元模型，有限元模型尺寸为55 cm×50 cm×4 cm，模型左端和上端为对称边界，右端为固支边界。由于爆炸荷载作用时间短，假定钢筋和混凝土之间黏结完好，采用分离式共节点方法建模，使用侵蚀算法实现材料失效的模拟，当混凝土或钢筋单元达到失效条件将被删除，钢筋和混凝土自动分离。钢筋和混凝土采用lagrange网格，网格尺寸0.25 cm，钢筋采用Beam161单元，共3 140个单元，混凝土采用Solid164单元，共70 400个单元，有限元模型如图2所示。

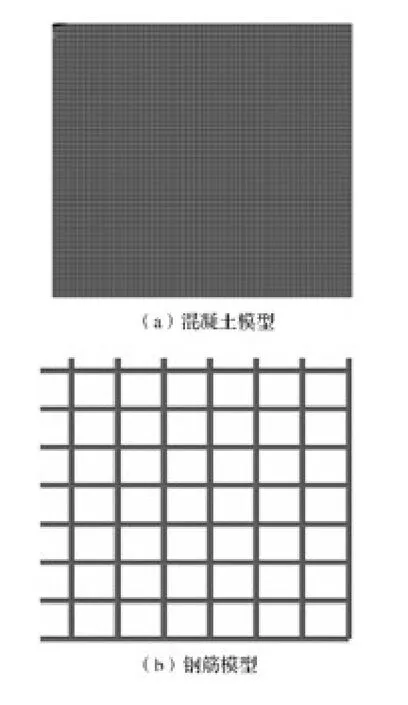
图2 1/4钢筋混凝土板有限元模型

2.2 爆炸荷载数值仿真

结构爆炸毁伤分析研究必须准确描述爆炸荷载强度，爆炸荷载强度与炸药当量、炸药与构件的相对位置等因素有关。爆炸荷载计算的常用方法有流固耦合(arbitrary lagrange-euler，ALE)方法和Conwep方法。经分析，在钢筋混凝土板爆炸毁伤研究中，Conwep方法相比ALE方法的优势在于:一是无需考虑爆炸冲击波在空气中的传递过程，无需建立炸药和空气单元，简化了研究内容，减少了建模工作;二是无需考虑流体和结构物的耦合作用，降低了模型复杂程度，降低了建模难度，提高了计算效率。本文采用Conwep方法进行爆炸荷载的计算和施加。

Kingery等［4］推导出计算球形空气爆炸和半球形地面爆炸的计算公式，由Randers等［5］改进并编入Conwep模块中，可在LS-DYNA中进行调用，Conwep进行爆炸荷载计算依据的数据来自于美国陆军技术手册TM5-855-1提供的经验公式和爆炸荷载曲线，能够执行多种常规武器爆炸效应的计算，包括各种空气爆炸、弹片和弹丸侵彻、成坑和地面的冲击，考虑了入射角、反射压力和入射压力等的影响，可表示为［6］

式中:P为爆炸荷载压力;Pr为反射压力;Pi为入射压力;θ为炸药起爆点到加载点连线与迎爆面法线方向的夹角。

可根据TNT当量、爆炸距离等计算空气中爆炸冲击波对结构的爆炸作用，计算结果与相关爆炸数据相符合，已经广泛地应用于工程中预测空旷场地结构上的爆炸荷载。

本文通过调用LS-DYNA中集成的Conwep模块，实现对不同TNT当量、不同位置的爆炸荷载仿真与加载。

2.3 材料模型及参数

(1)钢筋材料模型。钢筋采用MAT_PLASTIC_KINEMATIC，即双线性弹塑性模型，是一种各向同性、随动硬化或各向同性和随动硬化混合模型，近似模拟钢筋的弹塑性阶段，把塑性阶段和强化阶段简化为一条斜直线。可使用COWPER-SYMONDS模型，考虑应变率效应对材料强度及失效应变的影响，表示为

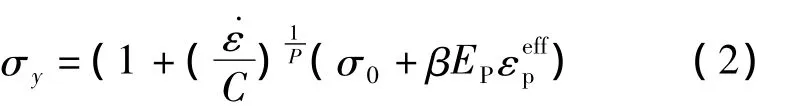
式中:σ0为初始屈服应力;˙ε为应变率;C和P为应变率参数;β为硬化参数;Ep为塑性硬化模量，分别为材料弹性模量和切线模量;ε为等效塑性应变。

试验中钢筋为HPB235，材料参数见表1。

表1 钢筋材料参数

(2)混凝土材料模型。混凝土采用MAT_CONCRETE_DAMAGE_REL3，即混凝土损伤模型，该模型使用初始屈服面、极限强度面和软化强度面3个强度破坏面描述混凝土材料的塑性性能［7］，考虑了弹性断裂能、应变率效应、约束效应等混凝土材料特性，分别表示为

最大失效面:

残余失效面:

初始屈服失效面:

式中:p 为静水压力;a0、a1、a2、a1f、a2f、a0y、a1y、a2y为材料常数，由无约束受压试验和三轴受压试验确定。

混凝土材料参数见表2。

表2 混凝土材料参数

3 数值仿真结果与试验结果对比

编号P 2-3钢筋混凝土板爆炸试验的破坏情况如图3所示，数值仿真的毁伤效果如图4所示，有效塑性应变云图如图5所示，爆炸试验结果与数值仿真结果的对比见表3。钢筋混凝土板动力响应试验中，炸药在距离板正上方爆炸，产生爆炸冲击波，冲击波到达板的上表面即迎爆面处，混凝土产生压缩破坏，应力波传递至背爆面，形成反射拉伸波并造成背爆面混凝土崩塌和层裂。钢筋混凝土板沿中心线发生明显弯曲破坏，迎爆面和背爆面均出现一定数量的环形裂纹和径向裂纹，迎爆面发生成坑现象，背爆面发生混凝土崩塌现象。钢筋混凝土板毁伤数值仿真模型完整模拟了爆炸荷载作用下钢筋混凝土板的开裂、裂纹扩展、双向弯曲、背面层裂崩塌等毁伤过程。

图3 P 2-3钢筋混凝土板爆炸试验破坏效果

图4 P 2-3试验数值仿真毁伤效果

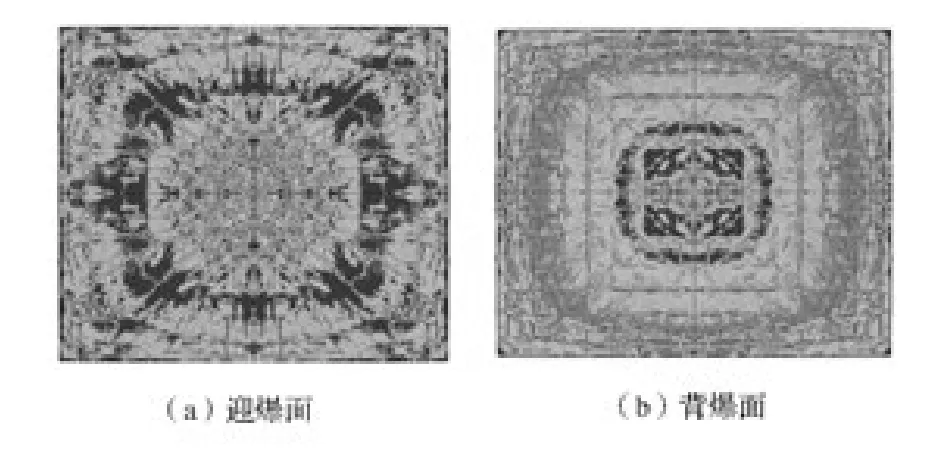
图5 P 2-3试验数值仿真有效塑性应变云图

表3 爆炸试验结果与数值仿真结果对比

可以从数值仿真结果的中心截面图中得出以下结果:支座转角 θ=3.68°，坑深为2.32 cm，中心截面毁伤程度为35%。其中支座转角的正切为中心点位移与单向支撑钢筋混凝土板半跨长之间的比值:

式中:x为中心点位移;L为单向支撑钢筋混凝土板跨长。

根据美国陆军技术手册TM5-1300确定损伤等级:0°～2°为轻度损伤;2°～5°为中度损伤;5°～12°为严重损伤。此钢筋混凝土板毁伤达到中度损伤。

从表3可以看出，板的成坑直径、层裂直径和中心点位移的数值仿真结果和试验结果比较接近，误差均在10%以内。从图3、4的对比可以看出，数值仿真中板中心的成坑、崩塌及背爆面层裂形态与试验产生的损伤很接近。由于试验中板两端的支撑不是完全固定，因而在数值仿真中，板边缘的裂纹破坏情况较试验更为严重。

数值仿真结果中背爆面崩塌情况比试验结果偏大，爆炸应力波在背爆面产生反射拉伸波，混凝土单元抗拉强度小于拉伸波强度，混凝土单元发生破坏，但由于混凝土材料的不均匀性，导致仿真结果偏大。

总体而言，钢筋混凝土板毁伤数值仿真模型的结果与试验现象匹配程度较高，较好地模拟了钢筋混凝土板正面成坑和背面层裂崩塌的破坏形态，数值仿真结果和试验数据基本一致，验证了爆炸荷载作用下钢筋混凝土毁伤模型的可行性。

4 钢筋混凝土板的破坏模式

为了研究不同爆炸荷载作用下钢筋混凝土板的破坏模式，利用数值仿真对不同当量下钢筋混凝土板的毁伤进行研究，爆炸距离为0.4 m，炸药当量分别为 250 g、460 g、750 g、1 000 g。数值仿真实验结果如图6所示，当量为250 g时，钢筋混凝土板表面出现细微裂纹，整体结构只发生轻度弯曲变形;当量为460 g时，钢筋混凝土板表面出现环形裂纹和径向裂纹，整体结构为弯曲破坏;当量为750 g时，钢筋混凝土板表面有大量贯穿性裂纹，中间区域发生冲切破坏，横向发生弯曲破坏，整体结构为弯剪破坏;当量为1 000 g时，钢筋混凝土板表面裂纹密布，中间区域冲切严重，横向弯曲变形很小，整体结构为剪切破坏。随着TNT当量的不断上升，爆炸荷载强度不断增强，钢筋混凝土板的破坏逐渐由整体弯曲破坏转变为局部剪切破坏。

图6 钢筋混凝土板破坏模式

5 结论

(1)使用Ansys/LS-DYNA软件，基于Conwep方法，建立并验证了钢筋混凝土板毁伤的数值仿真模型，该模型建模难度低，荷载施加简便，计算时间短、精度高，仿真结果与试验匹配较好，可以在大型建筑物爆炸毁伤机理研究中推广应用。

(2)随着爆炸荷载的增大，钢筋混凝土板表现为弯曲破坏、弯剪破坏和剪切破坏3种破坏模式，与相关研究相吻合。在建筑物结构抗爆设计中，需考虑3种不同破坏模式下的结构设计。

总体上看，钢筋混凝土爆炸毁伤数值仿真方法科学合理、可重复性高、实现成本低，为下一步大型建筑物爆炸毁伤的研究提供了重要借鉴，有力推动了交通重点目标抗爆设计和战时毁伤评估的研究。

［1］ 李忠献，师燕超.建筑结构抗爆分析理论［M］.北京:科学出版社，2015:序.

［2］ 汪维.钢筋混凝土构件在爆炸载荷作用下的毁伤效应及评估方法研究［D］.长沙:国防科技大学，2012.

［3］ 中国建筑科学研究院.GB 50010-2011混凝土结构设计规范［S］.北京:中国建筑工业出版社，2011.

［4］ Kingery CN，Bulmash G.Airblast parameters from TNT spherical air blast and hemispherical surface burst:ARBL-TR-02555［R］.U.S.Army BRL，Aberdeen Proving Ground，MD，1984.

［5］ Randers Pehrson G，Bannister K A.Airblast loading model for DYNA2D and DYNA3D:ARL-TR-1310［R］.Army Research Laboratory，1997.

［6］ David，Hyde W.Usery’s guide for microcomputer programs CONWEP and FUNPRO.Applications of TM5-855-1，“Fundamentals of protective design for conventional weapons”［R］.Final report，AD-A195 867，1988.

［7］ Malvar L J，Crawford J E，Wesevich J W，et al.A plasticity concrete material model for DYNA3D［J］.International Journal of Impact Engineering，1997，19(9/10):847-873.