车间运动学模型在智能车速度跟踪控制中的应用
李明喜,章永进,彭永胜,徐友春
(军事交通学院军用车辆系,天津300161)
车辆纵向运动速度跟踪控制是智能车技术领域的关键技术之一,主要研究内容是智能车的纵向控制子系统能够通过操纵油门和制动踏板调整车辆行驶速度,跟踪智能决策子系统所设定的目标速度,具备较高的控制精度和响应速度,是保证环境识别、智能决策技术实现的重要基础[1-2]。文献[3-4]对2011—2015年的智能车纵向速度控制技术现状进行了总结,指出目前常用的方法仍然是PID算法;文献[5]对目前车辆的纵向控制算法,尤其是应用在ACC自动巡航控制系统中的模糊PID算法进行了比较,结论是该类算法的适应性较差,难以在不同车辆间无障碍移植。纵观此类算法虽然具有计算简单、实现方便的优势,但适应范围受到限制,主要表现在这类算法通常和车辆自身动力学特性紧耦合[6],针对某一辆车进行反复整定和调整后,可以达到比较满意的控制效果,但是很难移植到其他车辆[1,4,7-8]。
本文尝试采用车间运动学预测模型,利用预测控制理论[4],实现智能车的纵向速度跟踪控制算法[5,7]。经试验证明,该方法可以有效规避车辆自身动力学的影响,便于在不同车辆间实现无缝移植,并具有良好的控制精度和响应速度。
1 基本原理
模型预测控制是利用系统的预测模型以当前时刻k所测量的系统状态为初值y(k),预测被控对象在将来时刻 i(1,2,…,Np(预测时域))被控变量的输出序列y(i|k)与设定值y0之间的差值,基于该差值采用“滚动式”优化策略计算出在开环条件下最优的控制输入序列u(i|k),将序列u(i|k)的前NC(控制时域)个量作为系统的实际控制输入。不断循环该过程,直到实际被控输出量y达到控制目标值y0的目标。该算法具有建模方便、对数学模型要求低、跟踪性能好等优点,因而更适合于智能车辆的纵向控制任务[5,8]。
在实现过程中,系统的预测模型是算法的基础,采用与车辆特性无关的车间运动学模型;优化算法采用Matlab中成熟的工具箱函数实现[9]。本文的重点是调整车间运动学模型的结构和确定预测时域Np,以达到降低计算成本、满足实时性的要求。
2 预测模型——车间运动学模型
车间运动学模型(如图1所示)是一种简单的描述两辆同向行驶的车辆之间位置变化关系的数学模型[3]。目标车辆的实际运动速度为vt(t),其主要变量有车间相对距离xr(t)和相对速度vr(t),可由安装在被控车辆前端的雷达测量获取,被控车辆的绝对速度vh(t)和加速度ah(t)由车辆自身传感器测量获取。因此,可以列出在初始时刻k(t=0)条件下车间运动学方程如下:

图1 车间运动学模型示意

设采样时间为Ts,对模型进行离散化,则

其中

式中k为预测周期序号,k∈N。
若控制量的变化量记为Δu(k)=u(k)-u(k-1),合并入上述方程,确定系统输出方程为y(k)=x(k),则离散后的车间运动学方程为
开挖洞口施工平台时,根据冲砂洞出口现场地形特点,在垂直洞口面高于顶拱2米以下以1:0.7的边坡形成开挖面,上部和侧边均以1:1的边坡形成开挖面。在洞口段采用3米150KN锚杆、Φ6 0.15x0.15 挂网和100mm厚的喷混凝土的支护措施,形成良好的施工作业平台。

其中

通过该模型,利用传感器测量得到当前时刻的状态x0,即可预测在输入u(k-1)时k(1,2,…,Np)个采样时刻的车辆运动状态xk,其中Np为预测时域长度。
从该模型所包含的物理参数可知,其优势在于能够反映车辆的运动状态,且和被控车辆的动力学特性无关,因此,可以满足不同类型车辆的运动控制,适用范围较广。
3 优化目标函数
根据模型预测控制的思想,智能车的纵向控制问题转化为:寻找一合适的输入序列uh(k),k∈N;满足条件min(xk-xref),其中xk为预测状态,xref为目标状态。下面介绍该优化问题的目标函数和算法。
3.1 目标函数
若状态偏差记为ξ=xe(k)=(xk-xref),该问题是一个标准的优化问题,优化目标可选为二次形式的标准目标函数:

式中:Q=Diag(q1,q2,q3,q4),qi(i=1,2,3,4),表示各个状态变量的权重;R为控制量输入的权重。
采用Matlab有约束的优化工具箱函数fmincon实现[4]。模型的约束条件:

式中u(k)=ah(k)为被控车辆需要的加速度,根据其方向和大小,依据油门制动联动控制逻辑,作为油门或制动的控制输入。安全性约束条件,是防止两车碰撞,保证两车之间的距离必须大于0;平稳性约束条件,是保证车辆加减速在一定范围|ahb|内,防止出现加速或减速过猛情况;舒适性约束条件,是保证车辆的加速平顺程度,约束加减速的最大增量jh,max,防止出现加减速窜动现象,提高车辆在纵向控制中的舒适程度。
上述的优化算法会求解出满足条件的最优的输入序列Δu(k),最终实现被控车辆以一定的速度 vh,ref跟踪目标车辆并保持相对距离 xr,ref。
3.2 基于单车控制的改进
上述优化算法可以满足多个约束、多个控制目标的最优控制,但是对于单个智能车并不适用,原因是不存在目标车辆。若假定被控车辆前存在有假想目标车辆,则该算法即可用于本车的控制,所假想的目标车辆特征是按照设定目标车速匀速运动。因此,车间运动学方程的输入参数即可以此确定。
此外限制加速度和加速度增量的约束条件的阈值也可以作为控制品质的调整参数使用,分为运动型、普通型、舒适性,以适合不同的工作情况。即输入 Δu'(k)=fΔu(k),其中 f为调节因子。
由于单车控制的目标是车辆能够达到稳定的行驶速度,因此速度状态变量的权重要明显高于车间距变量xr(k)和相对速度变量vr(k),可将后两者权重设置为0,即q1=q2=0,其目的是保证车辆的行驶速度为首要保证的优化目标。
通过上述的调整,基于车间运动学的预测控制算法即可在单车上实现车速的控制。
4 预测时域
目前,最优控制算法所面临的应用瓶颈是计算成本过高,难以满足实时控制系统的需要。预测控制算法优化目标的数量和预测时域的长度是影响其计算成本的两个重要因素,在3.2节通过将目标变量的权重设置为0,使得优化目标为2个,减少了计算成本。下面分析预测时域的确定。
预测时域是指在将来多长时间内利用预测模型计算车辆运动状态,主要有预测周期ts和预测周期数 Np[4]两个表示参数。
其中预测周期ts应该能够满足如下条件:即被控对象在一个预测周期内状态变量的变化量Δx能够被物理测量,即要求相应传感器的测量精度P要小于或等于Δx,才能够满足预测控制的要求。此外,为了保证满足该条件,还需要保留一定的裕量γ。而反映车辆状态变化的性能参数通常是加速时间 t,因此预测周期应满足的条件由下式确定:

预测周期数Np反映模型预测的时间长度,该参数直接影响着算法的精度和计算成本的大小。Np越长,状态预测的准确性越低,优化计算量越大;反之,预测精度会下降,计算成本则降低[5]。车辆是一个具有较大惯性的运动物体,在较长时间内的运动趋势是可以较准确地预测的,同时考虑计算设备的负载程度和计算任务,确定预测周期数Np时应当考虑如下经验条件:
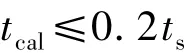
式中tcal为预测周期数为Np时预测过程的计算时间,ms,其大小需通过在实际的计算设备上测量获取。
综上所述,决定预测时域需要满足预测精度和计算成本两方面的条件要求。
5 试验验证
5.1 计算成本
计算设备配置为4核 CPU,主频2.7 GHz,内存4 G,Windows64操作系统,在不同预测周期和优化目标下的计算成本统计见表1。
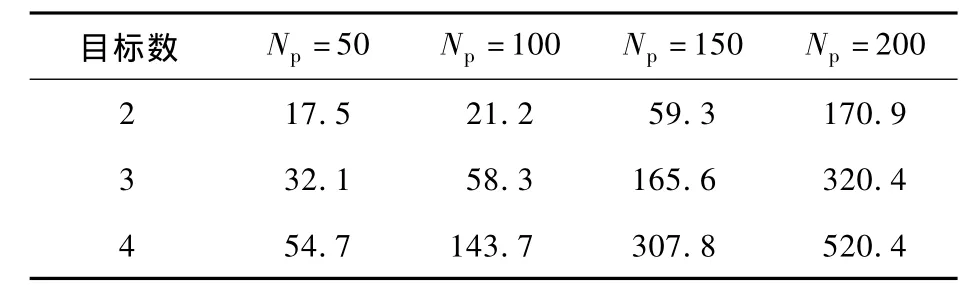
表1 计算成本 ms
由表1可知,在相同数量约束条件下,预测时域和预测目标的升高带来计算成本的成倍增加。但在单车预测控制中,两个目标、预测时域在100情况下的计算成本为21.2 ms,小于车辆实时控制周期为100 ms,能够满足实时控制的要求。
5.2 道路试验
在验证所设计的控制算法时,选择有纵向坡道的路面进行速度控制试验,试验数据如图2—5所示。
图2中曲线记录了实际速度跟踪目标速度过程中的变化情况,由数据分析可知:
(1)在目标车速稳定跟踪过程中,跟踪误差在±1 km/h范围内,跟踪程度在90%以上,达到了满意的跟踪要求;
(2)在加速段,速度跟踪偏差较大,其原因是考虑加速的舒适度要求,纵向加速度有效限制在0.2 m/s2以下(如图3所示),试验主观感觉舒适,跟踪程度在60%;

图2 实际速度与目标速度

图3 纵向加速度

图4 油门及油门调节增量
(3)在减速段,保证车速能够快速跟踪目标车速,保证避开障碍和定点停车,跟踪程度在75%。
图4曲线记录了发动机油门开度和油门调节增量变化情况,图5曲线记录了制动系统的压力和制动调节增量的变化情况,从数据分析可知:
(1)车辆发动机能够对预测控制增量产生实时的响应,证明控制时域的设置是合理的;
(2)对比油门和制动控制可知,加速过程中制动压力为5.2 MPa当量压力(制动系统剩余油压),在制动过程中,油门开度归零,反映系统油门制动的联动控制逻辑是有效的[7]。

图5 制动压力及制动调节增量
5.3 算法移植及应用
本文算法已经打包为可执行文件,并制定了函数接口,只需在目标机器上作为服务程序运行即可,移植快捷方便。目前已经在61所智能车团队的ix35智能车、宇通的智能客车上得到推广,获得了满意的效果。
综上所述,试验数据和应用情况反映了本文的预测控制算法是可行的,能够实现控制目标。
6 结论
(1)本文在车间运动学模型的基础上提出虚拟目标车辆的概念,使该模型可运用在单个智能车的纵向运动控制,规避了模型与车辆动力学特性的耦合问题,降低了控制系统设计难度,开发了具有较强适应性和较高跟踪精度的纵向控制算法,控制精度满足1 km/h的控制要求。
(2)通过对模型预测控制理论的研究,提出减少优化目标和确定预测时域的方法,能够将计算成本降低到系统分配的时间50 ms以内,可满足车辆实时性控制要求。
(3)在不同类型车辆的试验中的结果证明,该算法可以满足控制算法的无缝移植,具有一定的推广应用价值。
[1] Martinez J J,De Wit C C.A safe longitudinal control for Adaptive Cruise Control and Stop-and-Go scenarios[J].IEEE Transaction on Control Syst.Technology,2007,15(2):246-258.
[2] IUT De Longwy and Nancy-University.Design of speed and sensor bias estimator for Unmanned Aerial Vehicle[C]//2009 10th European Control Conference,2009:701-706.
[3] 徐友春,彭永胜,朱愿,等.FC2014常熟智能车未来挑战赛试验报告[R].天津:军事交通学院,2014.
[4] Ma W,Shi S.Extreme short-time prediction technology of high speed unmanned surface vehicle motion[J].Journal of Traffic and Transportation Engineering,2012,12(1):38-44.
[5] Shengbo L,Keqiang L.Model predictive multi-objective vehicular adaptive cruise control[J].IEEE Transations on Control Systems Technology,2011,19(3):98-112.
[6] Xiao J,Zhang W,Han Y.Fuzzy self-adaptive PID control in actuator control system of unmanned aerial vehicle[C]//IEEE:2011 Second International Conference on Mechanic Automation and Control Engineering,Hohhot,China,2011:223-226.
[7] Gerrit J L,Naus J P.A model predictive control approach to design a parameterized adaptive cruise control[C]//Automotive Model Predictive Control,Lncis 402,2010:273-284.
[8] Han bing S,Yumin S.Experimental investigation on longitudinal motion of high-speed unmanned surface vehicle[J].Journal of Shanghai Jiaotong University,2013,47(2):278-283.
[9] Kvasnica M,Grieder P,Baotic M.Multi-Parametric Toolbox·Matlab help[Z].2012.

