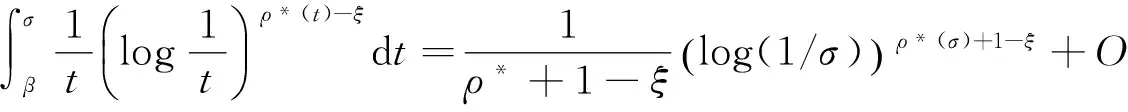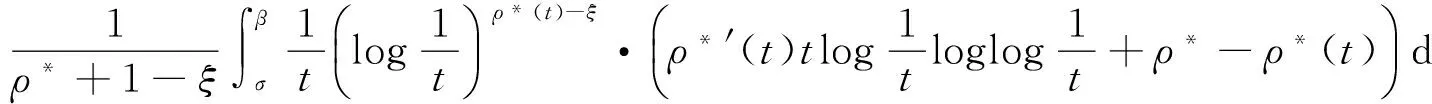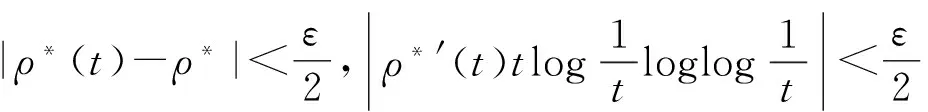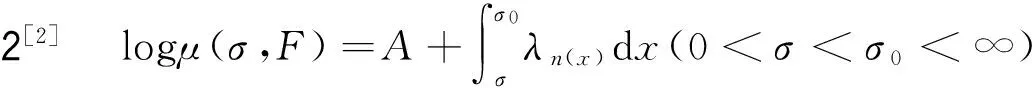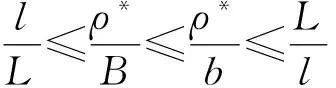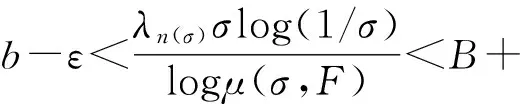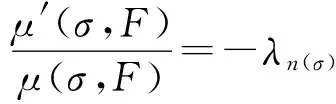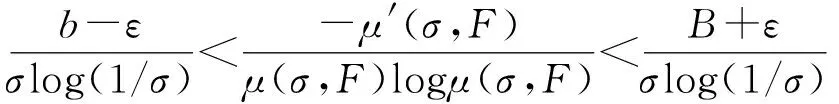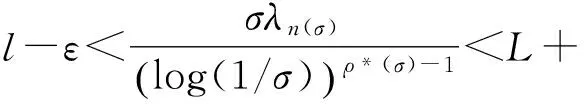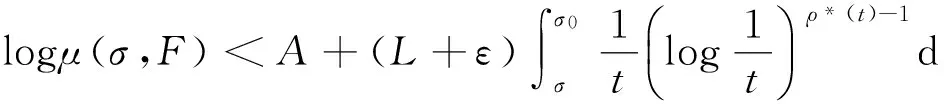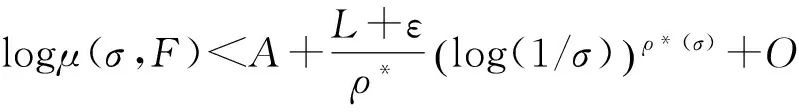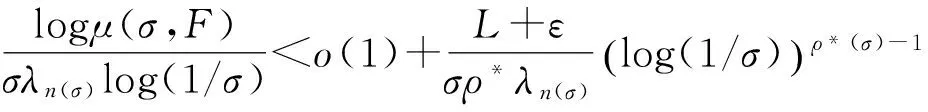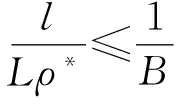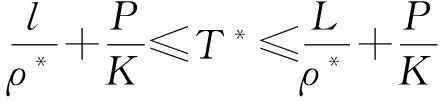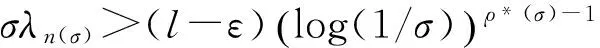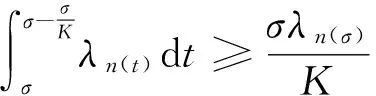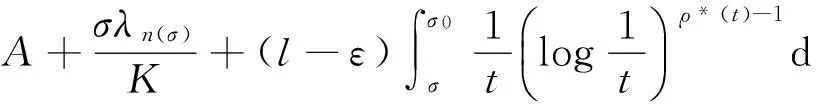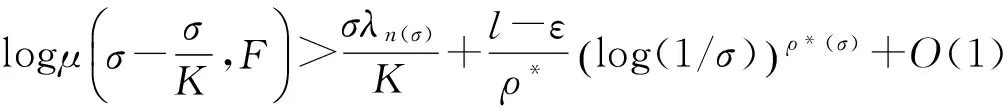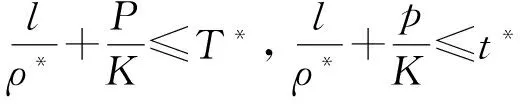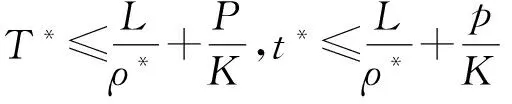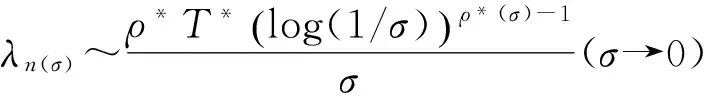半平面上解析的Laplace-Stieltjes变换的对数精确级
王金莲,陆万春
(1.江西师范大学学报杂志社,江西 南昌 330027;2.萍乡学院数学系,江西 萍乡 337055)
半平面上解析的Laplace-Stieltjes变换的对数精确级
王金莲1,陆万春2
(1.江西师范大学学报杂志社,江西 南昌 330027;2.萍乡学院数学系,江西 萍乡 337055)
利用对数精确级的定义,研究了右半平面上解析的Laplace-Stieltjes变换的对数精确级,得到对数精确级与最大模、最大项及中心指标的关系,推广了Dirichlet级数的相关结果.
对数精确级;Laplace-Stieltjes变换;最大项;中心指标;增长性
1 预备知识
考虑Laplace-Stieltjes变换所定义的函数
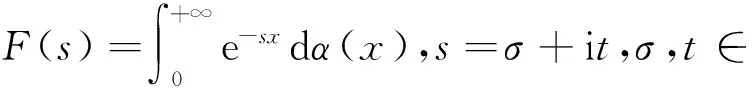
(1)
其中α(x)是对于x≥0有定义的实数或复数值函数,而且它在任何闭区间[0,X](0 作序列{λn}: 0=λ0<λ1<λ2<…<λn↑+∞, (2) 并且满足 (3) 记: (4) 时,其定义的函数F(s)在右半平面上解析,定义其增长级为[2] 当ρ=∞和ρ=0时,分别称变换(1)为无穷级和零级Laplace-Stieltjes变换.文献[3-5]利用型函数研究了无穷级Laplace-Stieltjes变换的增长性.文献[6-8]研究了零级Laplace-Stieltjes变换的增长性.为了进一步研究零级Laplace-Stieltjes变换的增长性,文献[2]定义了指数级Je(F)和下指数级Le(F),其中 文献[9]定义了对数级ρ*及下对数级λ*:对于F(s)∈D0, (5) 对于F(s)∈D0,文献[9]中还介绍了如下的对数型T*及对数下型t*: 定义1 称定义在(0,∞)内的实值函数ρ*(σ)为对数精确级,是指其满足条件: (ⅰ) 对所有满足0<σ<σ0<∞的σ,ρ*(σ)非负、连续、分段可微; 对于具有对数精确级ρ*(σ)的函数F(s)∈D0,定义其关于ρ*(σ)的对数型T*及下对数型t*为: 定义2 若0 在文献[10]中,作者把对数精确级和对数精确级的型推广到更加一般的情况.本文利用文献[11-12]的思想,通过对数精确级的定义,进一步得到对数精确级与最大项及中心指标的关系.设F(s)∈D0的对数精确级为ρ*(σ),记: (6) (7) (8) 引理1 设ρ*(σ)为对数精确级,则对于ξ<ρ*+1及0<σ<β<σ0,有 (9) 证明 由定义1,有 (10) 由(10)式,可得(9)式成立. 定理1 设F(s)∈D0具有对数级ρ*,下对数级λ*(1<λ*≤ρ*<+∞)及对数精确级ρ*(σ)→ρ*(σ→0),则有 b≤λ*≤ρ*≤B, (11) (12) 证明 由(8)式,对于任意满足0<ε 对上述不等式两边从σ0到σ积分,则有 (b-ε)loglog(1/σ)+O(1) 由(5)式,对充分小的σ,上述不等式两边同除以loglog(1/σ),并令σ→0,则(11)式成立. 根据(6)式,对任意满足0<ε (13) 由引理2,有 再由引理1,令ξ=1,则 对所有满足0<σ<σ0<∞的σ, 取极限得 (14) 利用(13)式右边的不等式,类似于(14)式的证明,可得 (15) 由(14)及(15)式易得(12)式成立. 推论 若L=l,则B=b=ρ*=λ*,即F(s)具有正规对数增长级. 定理2.2 设F(s)∈D0具有对数级ρ*(1<ρ*<∞)、关于对数精确级ρ*(σ)的对数型T*及下对数型t*,则对1 证明 由(6)式,对任意满足0<ε (16) 而且对1 (17) 因此,根据引理2,(16)及(17)式,有 (18) 用类似的方法,利用L的定义,容易得到 (19) 由(18)及(19)式可得定理2结论. 特别地,由于(18) 及(19)式对于满足1 定理3 设F(s)∈D0具有对数级ρ*(1<ρ*<∞),对数型T*及对数下型t*,并且对数精确级ρ*(σ)→ρ*(σ→0),则 l≤ρ*t*≤ρ*T*≤L. (20) 推论 如果 则F(s)是完全正规增长的,并且ρ*(σ)与T*=L/ρ*. 证明 由上述已知条件与(6)式,l=L=ρ*T*.再由(20)式得T*=t*=L/ρ*,故F(s)是完全正规增长的. [1] 余家荣.Laplace-Stieltjes变换所定义的整函数之Borel线[J].数学学报,1963,13(3):471-484. [2] KONG YINGYING,HONG YONG.On the growth of laplace-stieltjes transforms and the singular direction of complex analysis[M].Guangzhou: Press in Jinan University,2010. [3] 孔荫莹.半平面解析的无穷级Laplace-Stieltjes变换[J].数学学报,2012,55(1): 141-148. [4] 孔荫莹.平面解析的无穷级Laplace-Stieltjes变换[J].数学学报,2013,56(1): 53-60. [5] KONG YINGYING,SUN DAOCHUN.The analytic function in the right ha1f plane defined by Laplace-Stieltjes transforms[J].Journal of Mathematical Research & Exposition,2008,28(2): 353-358. [6] 陆万春,易才凤,贺妤函.关于全平面上解析的Laplace-Stieltjes变换的零级[J].数学的实践与认识,2013,46(6): 222-227. [7] 王金莲,陆万春.全平面上收敛的零级Laplace-Stieltjes变换的增长性[J].兰州大学学报(自然科学版),2013,49(1): 108-110. [8] 涂金,魏竞斯,徐洪焱.单位圆内[p,q]-φ(r)级解析函数与亚纯函数的级与型[J].江西师范大学学报(自然科学版),2015,39(2):207-210. [9] 徐洪焱,易才凤,胡伟.Laplace-Stieltjes变换所表示的解析函数的对数级与对数精确级[J].数学物理学报,2013,33A(2): 366-376. [10] LU WANCHUN.On the proximate type of an analytic function represented by Laplace-Stieltjes transformation[J].Journal of Mathematical Research with Applications,2015,35(1): 97-102. [11] 涂金,黄海霞,徐洪焱,等.单位圆内亚纯函数与解析函数的级与型[J].江西师范大学学报(自然科学版),2013,37(5):449-452. [12] 陆万春,易才凤.在矩控制下随机Dirichlet级数的(p,q)(R)型[J].江西师范大学学报(自然科学版),2012,36(5):482-486. (责任编辑:李亚军) On the logarithmic proximate order of analytic functions represented by Laplace-Stieltjes transformation WANG Jin-lian1,LU Wan-chun2 (1.Journal of Jiangxi Normal University,Nanchang 330027,China; 2.Department of Mathematics,Pingxiang University,Pingxiang 337055,China) By using the definition of logarithmic proximate order,the logarithmic proximate order of functions represented by Laplace-Stieltjes transformation,which are analytic in the half plane,is studied.And the relations which depict how the growth of maximum term is closely connected with that of central index and logarithmic proximate order are derived.Some results of Dirichlet series are improved. logarithmic proximate order;Laplace-Stieltjes transformation;maximum term;central index;growth 1000-1832(2015)04-0007-04 10.16163/j.cnki.22-1123/n.2015.04.002 2015-04-22 国家自然科学基金资助项目(11171170);江西省教育厅科技基金资助项目(GJJ13788). 王金莲(1963—),女,编审,主要从事复分析研究. O 174.52 [学科代码] 110·41 A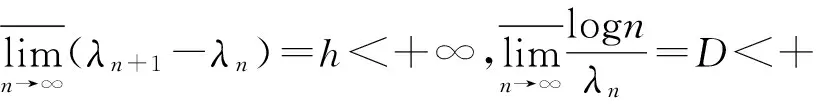
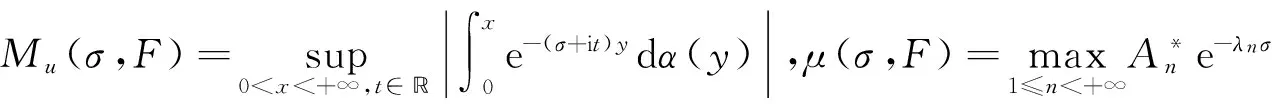
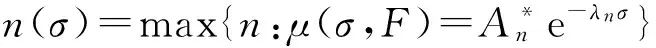
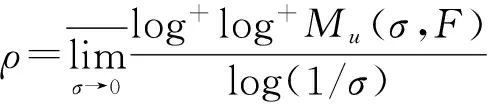
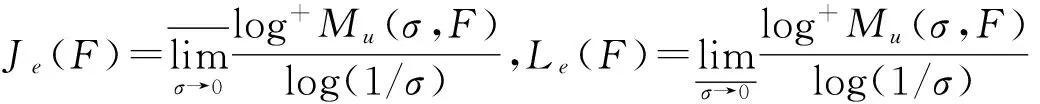
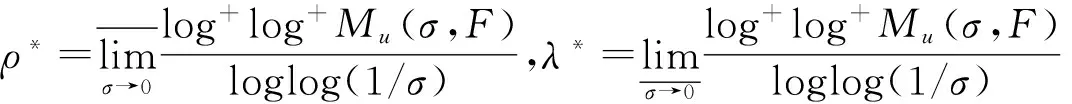
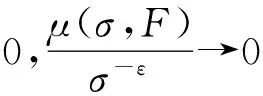
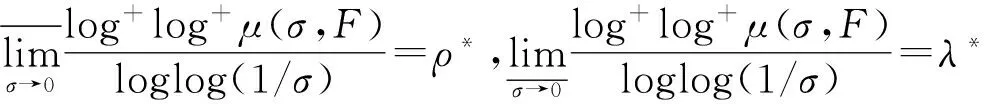
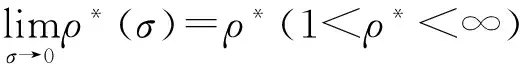
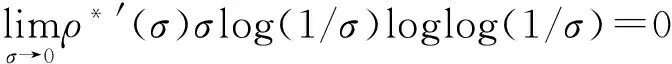
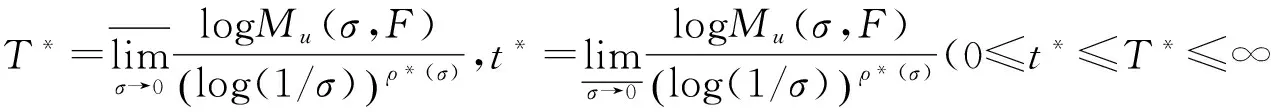
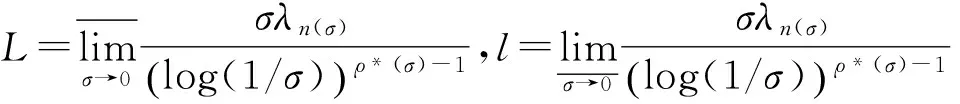
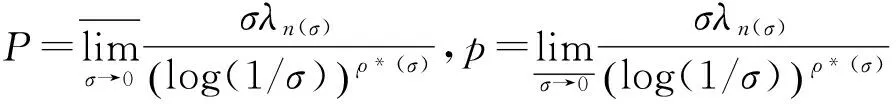
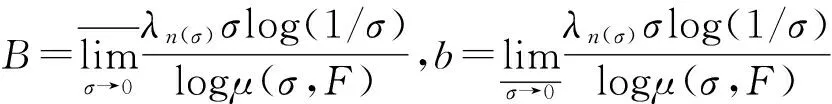
2 主要结果及证明