高程异常拟合模型在桥梁跨河水准测量中的应用

薛 涛，陈 辉

（南京长江第二大桥有限责任公司，江苏 南京 210038）

桥梁高程控制网布设具有控制范围大、涉及线路长且需统一江河两岸的高程系统的特点［1］。传统跨河水准测量，需要结合跨径大小和测区地形条件专门制定跨河水准观测方案，如采用倾斜螺旋法或经纬仪倾角法还需要制作特定的观测觇板，采用测距三角高程法对天气要求条件较高且所需观测时段较多［2］。目前GPS技术得到了迅猛发展，其平面定位精度采用相对静态定位可达到1~2 mm，高程定位精度也达到厘米级，为GPS高程转化为正常高程提供了前提。大型桥梁高程控制网对跨河水准测量的精度要求较高，提高跨河点正常高程的转换精度关键取决于测区高程异常的拟合效果。

1 高程异常拟合模型

常用的高程拟合方法有地球重力场模型法、几何内插法以及神经网络法，重力模型法需要重力观测资料，一般生产单位难以获得，本文不予讨论。

1.1 几何内插模拟法

几何内插法是从数学解析式的角度出发，其基本思想是：对GPS控制网的测站点进行GPS大地高测量，得到测站点的大地高 ，然后在控制网中选取部分点进行几何水准测量，得到部分测站点的正常高 ，根据这些点的大地高和正常高求得高程异常 ，然后建立数学函数模型，从而拟合出该控制网测区范围内的似大地水准面；根据GPS测量得出的未知点的平面坐标，通过内插的方法求得未知点大地高与正常高的关系（称为高程异常 ）求出地面点的正常高。下面选取曲线和曲面拟合法中具有代表性的方法进行论述。

（1）多项式曲线拟合法［3］

多项式曲线拟合法所采用的拟合模型为一个m次一元代数多项式。解算拟合函数模型的方法为：假设GPS测点的高程异常ξi与其平面坐标xi（或yi）间的函数关系式为：

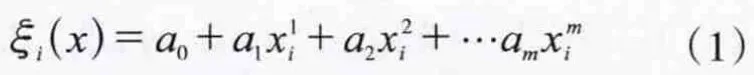
各已知点的高程异常与根据拟合模型求出的高程异常之差为：

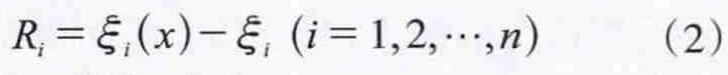
根据最小二乘法，应在

的原则下，求得（1）式中的待定系数 ，即可求得任意一未知点的高程异常。拟合函数模型中代数多项式的次数并非越多越好，因为拟合曲线的波动会随着代数多项式次数的增加而增大，常数值会出现不稳定的现象。插值多项式的次数应根据测区的长度和地形等级要求而定，一般取前3项即可。

（2）多项式曲面拟合法

一般用下列数学表达式作为多项式曲面拟合的函数模型：

式中：ai（i=0，1，2…，n）为待定系数。

假如有n个已知点，式（4）可以写成下列矩阵形式：

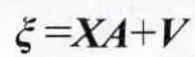
式中： ξ =［ξ1ξ2…ξn］T，A=［a0a1…an］T，V=［v1v2…vn］T；

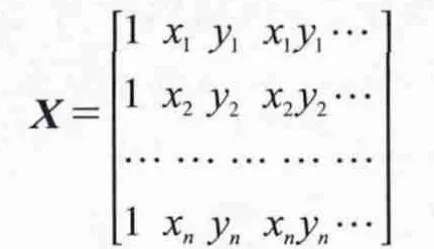
根据最小二乘原则，求得：A=（XTX）-1XTξ，然后带回到式（4），就可以求出待定点的高程异常值ξ。

在式（4）中，假如取前3项，则拟合函数模型为平面拟合，已知点个数不得少于3个；若取前6项，则拟合函数模型为二次曲面拟合，已知点个数不得少于6个。对于测区范围不大的工程应用，一般采用二次曲面拟合方法。

1.2 BP神经网络法

BP网络的结构分为3层，其中包括输入层、输出层和隐含层（隐含层层数可以自由设定）［4-6］。输入层节点的个数通常取输入信息的维数，输出层节点的个数通常取输出信息的维数。基于BP神经网络GPS高程拟合模型的输入层节点数一般设置为2，为已知点的平面坐标（x， y）；输出层节点数一般设置为1，为已知点的高程异常 。隐含层目前还没有统一的理论解析式设置其节点的个数，常用的方法为通过反复试验，然后得到最合适的隐含层节点数。

1.3 模型精度评价指标

根据参与检核点的高程异常值 pi和拟合出的高程异常值 pil，计算其拟合残差：Vi= pi- pil ，外符合精度的计算公式为：式中：n为参与检核点计算的点数。

2 工程应用

2.1 工程概况

某大型斜拉桥项目线路全长7.6 km，主桥主跨400 m。选取主桥跨河两侧的控制点进行GPS高程测量传递，在靠近主桥两岸各选择8个观测条件较好的控制点作为GPS高程拟合的试验点（图1），F15、F18 2个点为主桥建设的重要高程控制点，为2个强制对中观测墩，跨河高程测量主要在这2个点上进行。

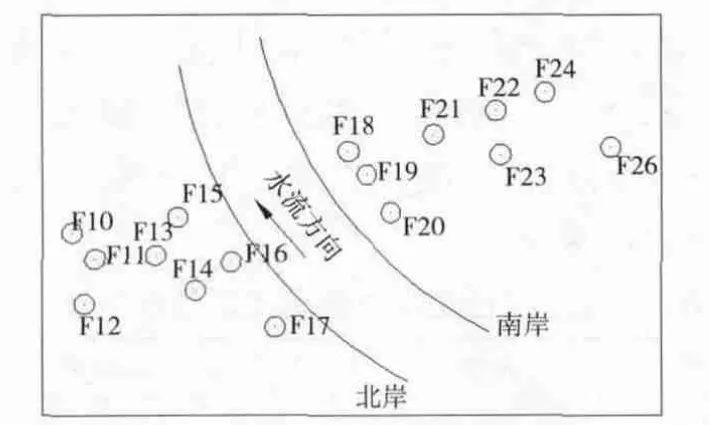
图1 试验场地点位分布图

试验点大地高程以WGS-84参考椭球面作为基准面，各点位相应大地高程和正常高程见表1。

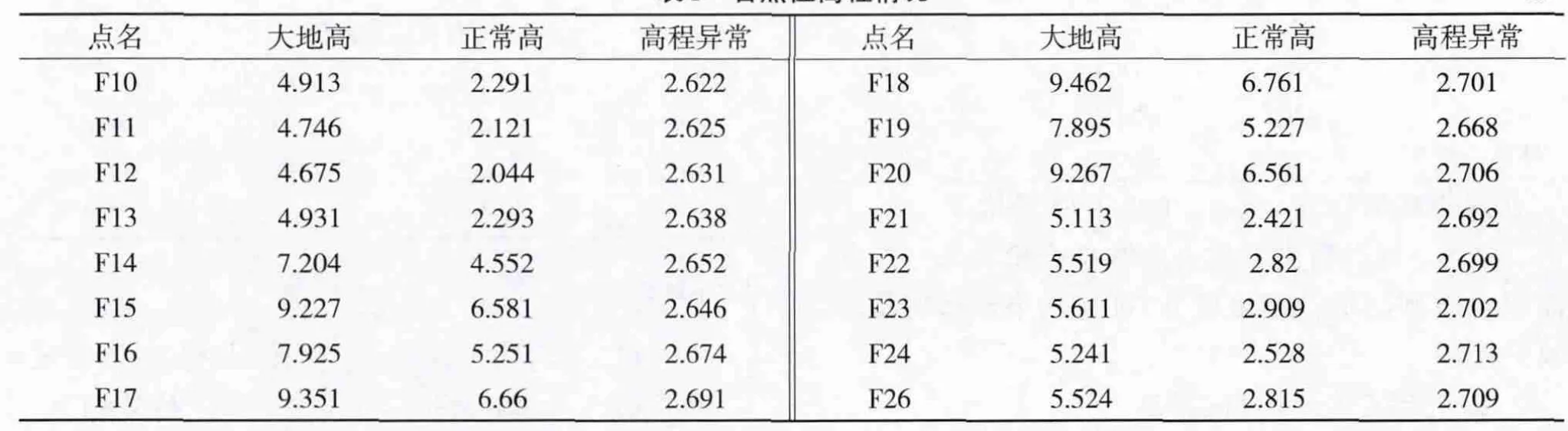
表1 各点位高程情况 m

图2为高程异常曲面变化图，其中x、y为控制点坐标，z为各点高程异常。由图2可以看出南岸高程异常曲面变化相对北岸较缓和。

图2 高程异常曲面图

2.2 不同高程异常拟合模型的拟合效果比较

分别采用多项式曲线拟合、二次曲面拟合、BP神经网络方法进行测区高程异常的拟合，并对已知点的选取采用不同的方案来拟合。

（1）南岸拟合北岸（试验1）

常规的拟合方法，在两岸只有一个水准基准点的情况下，另一岸的高程需要从这一岸进行高程传递。以南岸的高程控制点作为已知点，拟合北岸的高程控制点，结果见表2。

表2 南岸拟合北岸点位高程异常差值对比 mm

从表2可以看出多项式曲线拟合模型和二次曲面拟合模型的拟合精度较低，神经网络模型的拟合效果较好。

（2）北岸拟合南岸（试验2）

用北岸的8个已知点拟合南岸的8个未知点，结果见表3。相对于试验1，通过北岸控制点高程异常拟合南岸点位中多项式曲线拟合精度有明显的提高，但二次曲面拟合模型的拟合精度降低，说明在试验中二次曲面拟合得出的似大地水准面与真实的似大地水准面差距太大，已知点的选取对二次曲面拟合模型精度的影响很大，二次曲面模型并不适用于此次试验。神经网络模型的拟合效果较试验1稍微降低。

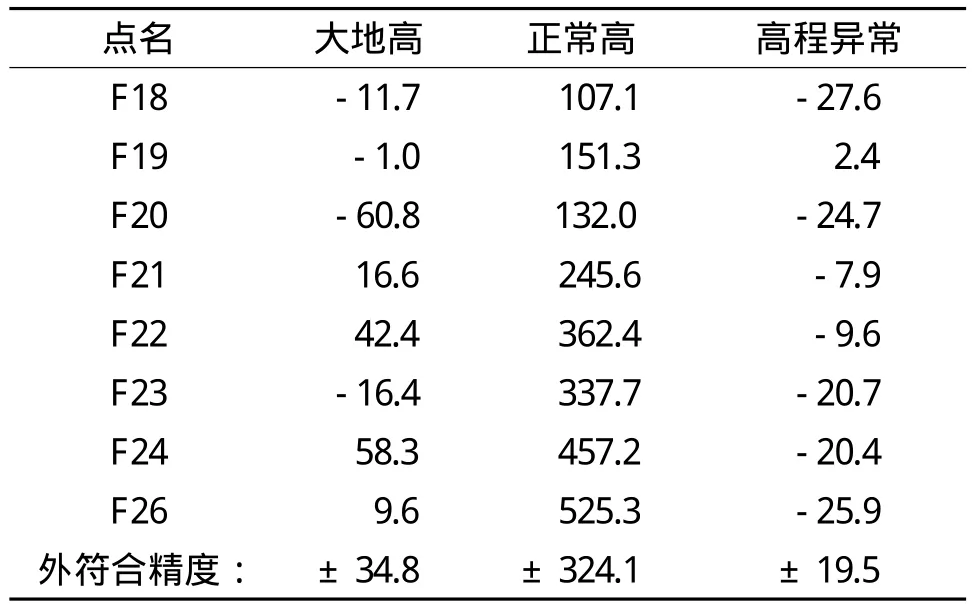
表3 北岸拟合南岸点位高程异常差值对比 mm

（3）利用两岸已知点拟合跨河点（试验3）

以一岸的已知点进行GPS跨河高程拟合精度较低的原因在于：以一岸的控制点作为拟合模型的已知点，点位分布不均匀，以此所创建的高程拟合模型无法反映出另一岸的地形特征，从而导致拟合模型的精度较低。为此将F15和F18 2个点作为未知的高程拟合点，然后将这2个点周围剩余的14个点作为已知点进行GPS高程拟合，结果见表4。F15和F18 2个点相距780 m，4等水准限差为 17.7 mm，3等水准限差为 10.6 mm。

试验3表明几种拟合模型的精度都有了较大的提高，说明通过两岸已知点来单独拟合跨河点可以明显提高跨河点正常高的转换精度。但是，多项式拟合以及二次曲面拟合模型的精度还是没能达到三等水准，无法满足本文试验场地跨河施工控制网测量的精度要求，BP神经网络拟合已达到三等水准测量要求。

表4 高程异常差值对比 mm

3 结论

本文以国内某大型桥梁高程控制网为例进行试验，重点研究高程异常拟合模型在 跨河水准测量中的应用，制定不同的试验方案，得出如下结论：

（1）桥梁高程控制网控制的线路较长且跨越江河后其高程异常曲面往往发生改变，本项目中南岸区域高程异常曲面变化较缓和，北岸的高程异常变化则相对较陡。

（2）在利用河流一岸的控制点拟合出的高程异常模型求对岸控制点正常高程时，几何内插法中的多项式曲线方法和二次曲面拟合方法效果较差，而BP神经网络算法精度较好，说明单独采用一岸控制点拟合整个线路区域的高程异常变化的方法不可取，同时也说明BP神经网络算法的适应性较强。

（3）利用两岸控制点分别拟合跨河点的正常高程时，得到了较好的效果，尤其是BP神经网络算法达到了3等跨河水准的测量精度。本文试验结果可供类似桥梁工程参考，未来研究方向可放在改进的BP神经网络算法对高程异常的模拟效果上。

［1］周世林，吴迪军.GPS桥梁施工控制网设计及应用分析［J］.铁道勘察，2009（6）：8-10.

［2］JTG C10—2007公路勘测规范［S］.

［3］李景卫，杨荫奎.GPS高程拟合中多面函数及二次曲面函数的比较与分析［J］.山东冶金，2006，28（3）：42-43.

［4］Wen Xiulan. Evolving Neural Networks Using an Improved Genetic Algorithm［J］. Journal of Southeast University，2002，18（4）：367-369.

［5］曹先革.基于人工神经网络的GPS高程异常拟合方法研究［D］.武汉：中国地质大学，2008.

［6］鲁铁定，周世健，臧德彦.关于BP神经网络转换GPS高程的若干问题［J］.测绘通报，2003（8）：7-10.

［7］闻新，周露，王丹力，等.MATLAB神经网络应用设计［M］.北京：科学出版社，2001.

［8］黄纪晨.GPS跨河高程测量分析与研究［D］.南京：河海大学，2011.

［9］李胜.GPS高程异常拟合研究［D］.大连：大连理工大学，2006.