PC连续箱梁优化设计及系统开发

刘桂林

（中铁第四勘察设计院集团有限公司，湖北 武汉 430063）

G.Magnel于1948年首次提出PC结构受弯截面预应力最优化设计。早期研究中，主要针对简支空心板梁、T梁进行优化设计，在工程实践中，已取得了显著的效果［1］。

对于PC连续梁的优化设计，目前主要针对小跨度连续梁桥，或者满足某些特定条件下（梁体截面尺寸确定、施工工艺确定）的结构。但设计变量考虑不够全面，优化模型与结构分析程序之间连接不够紧密，自动优化程度不高。故建立完善的PC连续梁优化模型，开发自动优化系统，对于PC连续梁桥的优化设计具有重要意义［2-3］。

1 PC连续梁的优化设计

PC连续梁优化设计包括结构参数的选取与预应力筋的估束。针对连续梁桥的自动估束，以往优化设计中，需要以上、下缘截面钢束作为其中一个设计变量，总造价或者钢束总量作为目标函数，控制截面应力作为约束条件，通过优化算法进行求解。

1.1 设计步骤

目前通过结构分析程序可以实现连续梁的估束功能，不同结构参数下的连续梁，对应不同数量的钢束。基于该理念，本文提出连续梁桥自动估束的一种新方法：由优化模型不断地修改设计变量，借助结构分析程序进行连续梁的估束与应力、挠度、剪力（以下统称“效应”）的计算，以此作为约束条件，最终求得目标函数的最优解。

具体步骤如下：

（1）将初始设计变量代入结构分析程序，进行连续梁的第一次估束与效应计算；

（2）估束得到的预应力筋与全桥混凝土总造价作为优化模型的目标函数，计算效应不超过允许值作为优化模型的约束条件，建立优化模型；

（3）求解优化模型，若目标函数并非最优解，则由优化模型修改设计变量，将第2组设计变量代入结构分析程序进行第2次估束与效应计算，再次执行步骤（2）、（3），如此反复循环迭代，直到求得最优解。

1.2 优化设计变量的确定

（1）跨中、支点梁高（KZH0，ZDH）；

（2）跨中、支点处底板厚（BH0，ZBH）；

（3）底板上、下缘抛物线次数（DD，OO）；

（4）腹板变化厚度（FH1，FH2）；

（5）腹板厚度变化位置距中支点的距离（FHL1）；

设计变量确定为：

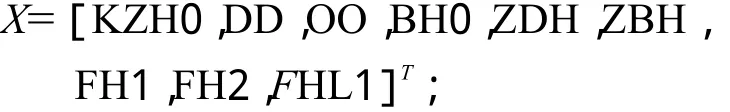
通过对国内外两百多座变截面连续梁桥进行统计，得到上述设计变量的取值范围。

（1）跨中梁高/中跨长度：

KZH0/ZKL0=1/30~1/55；

（2）底板下缘抛物次数：DD=1.2~2.5；

（3）底板上缘抛物次数：OO=1.2~2.5；

（4）跨中底板厚度：BH0=25~35 cm；

（5）支点梁高/中跨长度：

ZDH/ZDL0=1/16~1/25；

（6）腹板变化厚度：FH1、FH2= 30~150 cm。

连续箱梁截面如图1所示，由于连续箱梁截面涉及变量较多，仅以9个关键因素作为设计变量，其他变量需在优化之前指定，由此便可计算出任意截面的特征值。

图1 箱梁截面示意图

1.3 约束条件

为了保证结构运营安全可靠，需控制结构在使用过程中的应力、挠度、剪力，以此作为约束条件。本文还同时考虑了剪切应力作为约束条件，以保证箱梁在使用过程中不会发生腹板剪切破坏。

（1）梁体应力约束

（2）梁体位移约束

式中：fmax" ,为静活载作用下梁体最大位移列阵；f6@为梁体位移限值。

（3）梁体剪力约束

由于本程序并不能够考虑纵向预应力束弯起部分对剪力的影响，故而将预应力混凝土结构当做普通钢筋混凝土结构进行抗剪验算。

式中：Vd",为承载能力极限状态基本组合下，单元左右截面最大剪力列阵；b",为单元左右截面腹板宽度列阵；h0",为单元左右截面有效高度列阵。

1.4 目标函数

以混凝土和钢束造价之和作为优化目标函数，即：

式中：C1、C2分别为混凝土单位体积造价和用量；G1、G2分别为钢束单位重量造价和用量。

1.5 优化算法

本模型采用混合整型二次规划法程序（MIQL）进行求解［4-5］。MIQL主要求解严格的凸形混合整型二次规划问题，该问题的线性等式和不等式约束及目标函数如下：

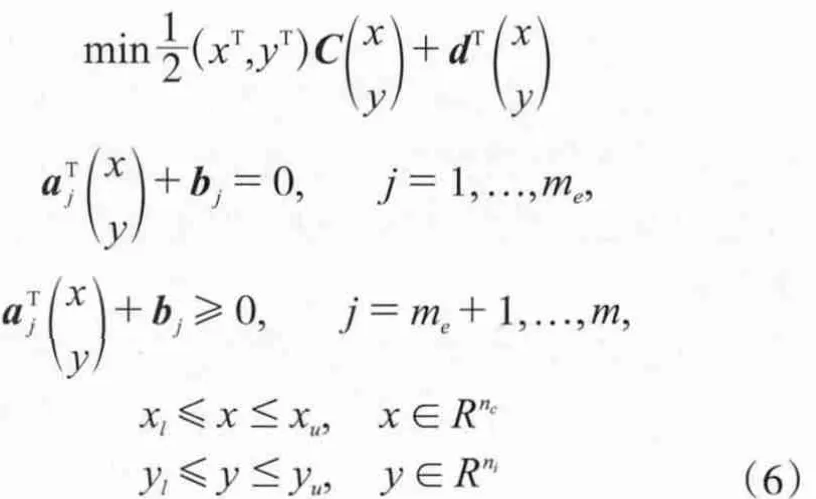
式中：C为n×n阶正定矩阵；n=ni+nc；d为一个n维列向量；a为m×n矩阵；b为m维列向量。xl，xu，yl，yu分别为连续变量x、整型变量y的上、下界。为了符号统一，这里引入两个索引集I和J，I , J = "1 , f ,n,，I , J = Q ，当 yk! N, k ! I 时，I = ni，同样当 xl!R,l ! J时，J = nc。

如果ni＞0，那么形如式（6）的混合整型二次规划问题可以通过分支切割法求解。目前该程序已经应用了补余圆整割平面和离散割平面两种不同的割平面法。

1.6 结构分析程序

由于MIQL优化程序在运行时，需要不断读入不同设计变量值下的约束条件值及目标函数值，以求得约束条件及目标函数对设计变量的导数值。对于PC连续梁的优化计算，约束条件值及目标函数值的获得需要通过结构分析计算获得，而目前大型商业桥梁计算软件都没有向用户开放调用其分析程序的接口，故无法利用这些软件进行优化计算。本文根据有限元一般方法及桥梁施工、计算的特点改编了连续梁结构分析程序，以满足优化过程中结构重分析的需求。

本结构分析程序能够实现如下功能：自重及二恒内力计算；附加荷载（整体升、降温）内力计算；活载内力计算；成桥阶段预应力估束计算［6-7］。

2 悬灌连续箱梁桥自动优化系统［8-10］

本文提出的优化模型规模较大，优化过程需反复调用结构分析程序，故采用计算效率较高的FORTRAN语言编写本系统内核，利用VB进行程序界面设计，程序运行时调用DLL(动态数据连接库)函数，采用本方法既能增加程序的计算速度，也能增加程序的可操控性。系统程序编译流程如图2所示。

该系统包含总体信息、箱梁信息、梁段信息、横隔板信息、使用信息、优化信息6个子界面。前5个子界面用于确定连续箱梁的相关结构建模参数，最后一个子界面用于确定优化建模参数。

该优化系统适用于箱梁构造的3跨悬灌连续箱梁桥，只需在程序界面中输入相关设计参数的初值，设计变量及约束条件的限值，即可进行自动优化设计。另外为了保证优化设计的成果满足规范限值条件下并留有一定安全储备，可以对约束条件的限值进行调整（高于规范标准）。

图2 程序流程图

该系统可以实现如下功能：（1）得到最终优化目标函数以及对应的设计变量值；（2）生成绘制优化后连续梁截面、梁体立面图的lsp语言；（3）生成优化后的连续梁在桥梁博士（Dr. bridge V3.0）中建模的脚本文件。

3 实例分析

3.1 耒水桥概况及优化建模

本文以一座已经运营的3跨悬灌连续箱梁桥耒水桥为例，对本系统进行验证。耒水桥主跨为65 m+115 m+65 m，桥宽29 m，分上下两幅。梁段划分可直接指定，当设计人员选择程序自动分段时，程序按“4 m段数→3.5 m段数→3.0 m段数”来处理悬灌节段数。耒水桥离散单元总数为86个，优化模型中应力约束条件数为688个，位移条件约束数为87个，抗剪能力约束数为344，优化求解收敛精度取值0.1。

3.2 优化结果

优化结果表明，耒水桥底板厚度，跨中、支点梁高，底板顶、底缘抛物线次数均发生了较大变化，优化前后设计变量、目标函数的对比如表1、表2所示。

3.3 优化结果验证

优化计算结束后，本系统将会输出结构参数经过优化后的全桥有限元模型脚本文件，将该文件导入到大型通用商业桥梁专业软件桥梁博士（Dr.bridge V3.0），即可在桥梁博士中完成全桥模型的建立。导入脚本文件后在桥博中形成的全桥模型如图3所示。

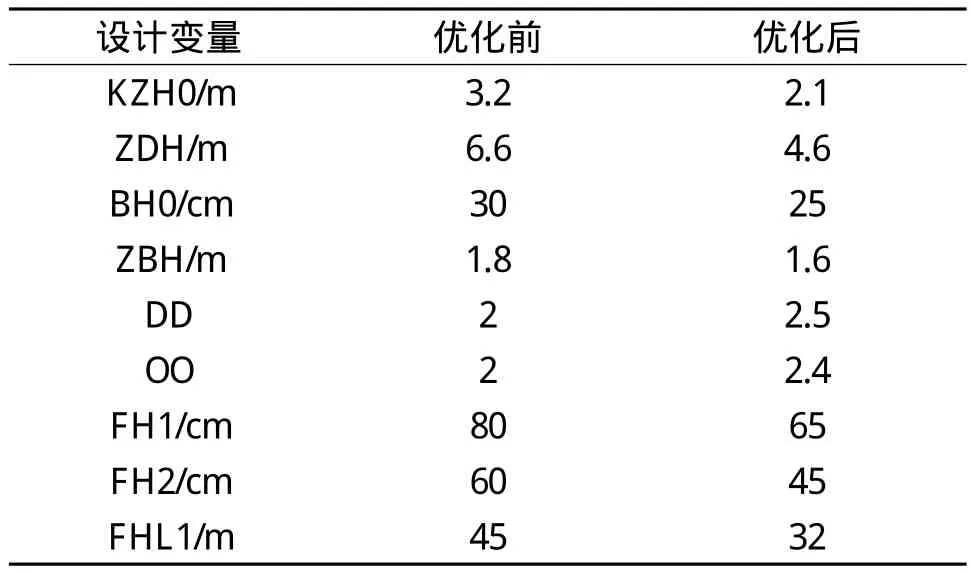
表1 优化前后设计变量对比表

表2 优化前后材料用量对比表

本系统按正常使用极限状态下标准值组合进行钢束估算，并会计算布置钢束后主梁截面的应力。桥博中进行钢束估算计算后，会输出承载能力极限状态、正常使用极限状态两种状态下的各单元左右截面上下缘钢束用量，但不计算布置钢束后主梁截面的应力。

本文列出部分截面钢束用量，从表3中可以看出本系统输出的优化估束面积和桥梁博士对优化模型进行估束计算后的面积基本相同，说明本系统的优化估束功能正确。

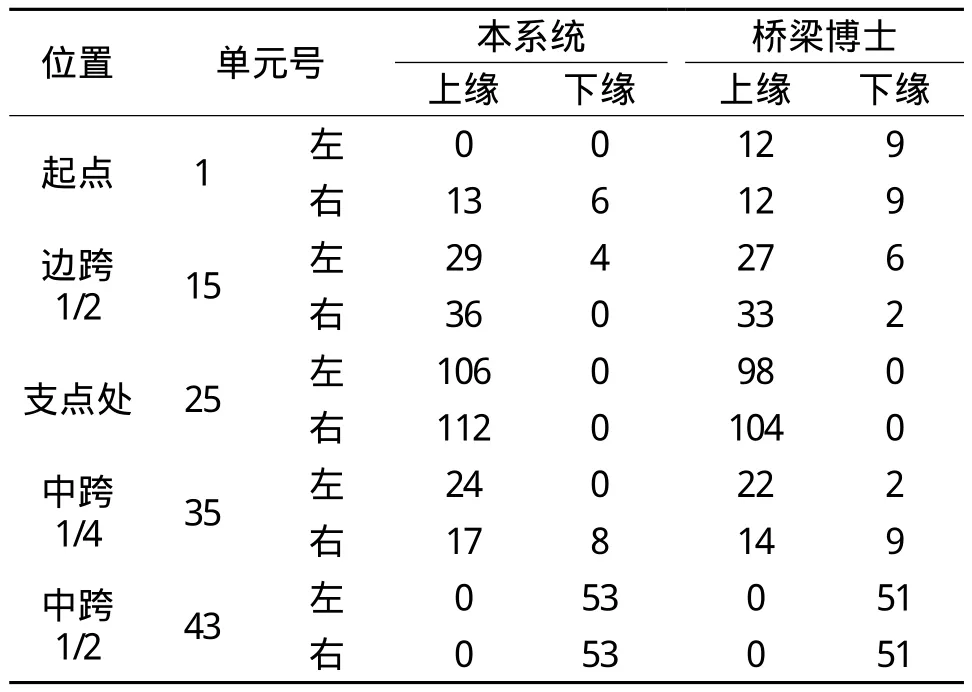
表3 部分截面钢束用量对比表

本系统按估算钢束配置后，主梁在正常使用极限状态标准值组合下，截面上下缘最大、最小应力（仅示意半桥），压应力为正，拉应力为负。如图4、图5所示。

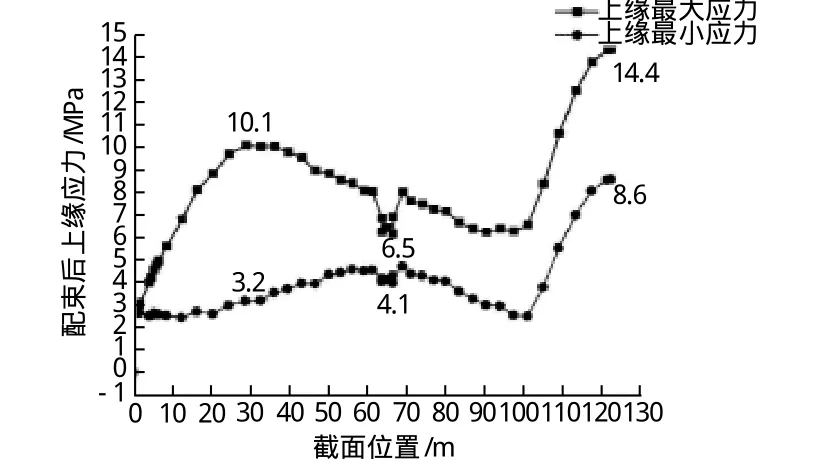
图4 耒水桥配束后正常使用极限状态标准组合下截面上缘正应力

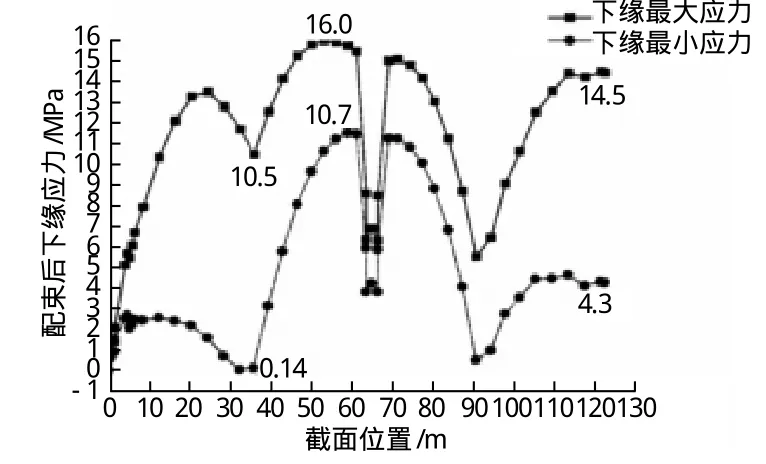
图5 耒水桥配束后正常使用极限状态标准组合下截面下缘正应力

从图4、图5可以看出，优化后截面考虑配束效应后，正常使用极限状态标准组合下的截面上下缘最大、最小应力均小于0.5Fck，且最小应力均大于0（不出现拉应力），说明优化模型中的约束条件起到了很好的控制。

耒水桥优化前后承载能力极限状态基本组合下的内力如图6~图8所示。从图中可以看到，优化后的模型较原设计截面弯矩减小，说明结构受力更加合理；本系统计算结果与桥梁博士软件计算结果基本相等，再次验证了本系统的准确性。

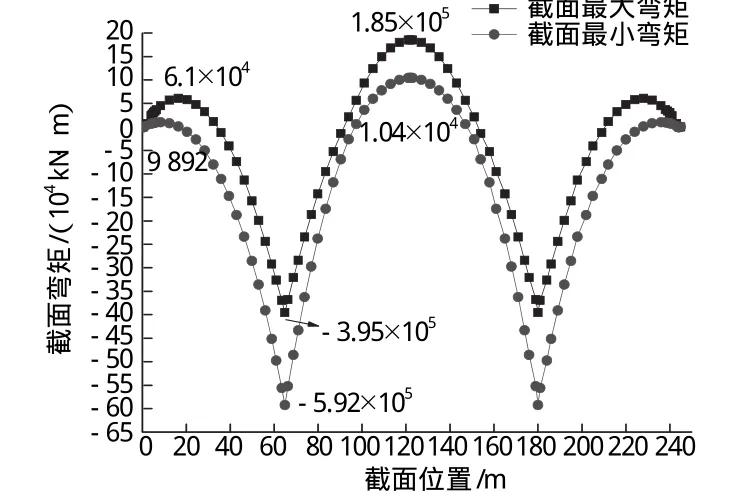
图6 本系统输出的耒水桥优化后承载能力极限状态基本组合下截面弯矩

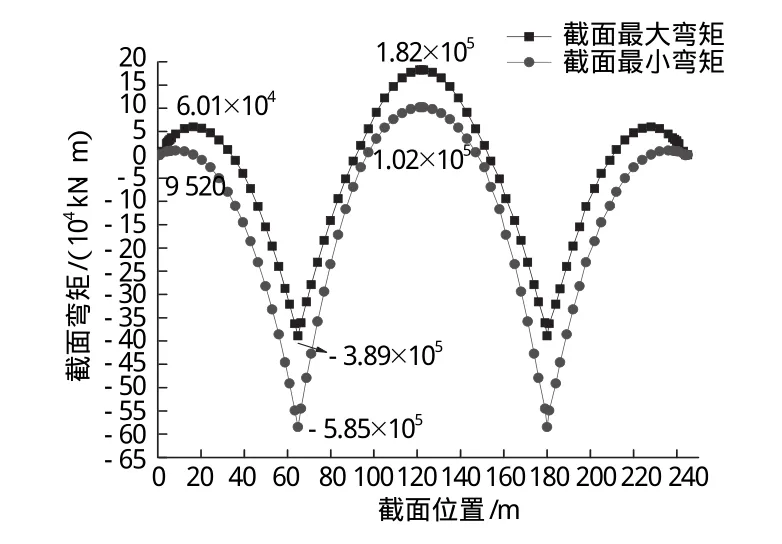
图7 桥博输出的耒水桥优化后承载能力极限状态基本组合下截面弯矩

图8 原设计耒水桥承载能力极限状态基本组合下截面弯矩

4 结论

本文针对PC连续梁桥，建立了优化模型，并结合结构分析程序进行了自动优化系统的开发，设计人员只需给定材料等级、跨度、荷载情况等少量数据，系统即可完成自动建模和优化设计。本系统自动化程度较高、通用性强，能够进行连续梁的优化设计，实现自动估束的功能；能够绘制优化后连续梁截面、梁体立面图；生成连续梁在桥梁博士（Dr. bridge V3.0）中建模的脚本文件，用于结构检算以及精细设计。

以耒水桥为例，梁体高度、腹板厚度相比原设计均有较大降低，梁底曲线形式也与原设计不同，梁体总造价相比原设计下降20.1%， 说明本文提出的优化模型效果明显，自动化程度高。

［1］ 杨永清，陈国藩.预应力混凝土连续梁的优化设计［J］.西［1］南交通大学学报，1990，12（4）：23-29.

［2］ 赵新.预应力混凝土连续梁结构优化设计［D］. 南京：河海［1］大学，2008.

［3］ M. A. Utrilla，A. Samartin. Optimized design of the prestress in［1］continuous bridge decks［J］. Computers and Structures，1997，［1］64（1）：719-728.

［4］ Balas Egon，Perregaard Michael. A precise correspondence［1］between lift-and-project cuts，simple disjunctive cuts， and mixed［1］integer Gomory cuts for 0-1 programming［J］. Mathematical［1］Programming，2003，94（2）：221-2245.

［5］ Schittkowski K. Optimal parameter selection in support vector［1］machines［J］. Journal of Industrial and Management Optimization，［1］2005，1（4）：465-476.

［6］ 徐光辉，胡明义.公路桥涵设计手册 梁桥（下册）［M］.北［1］京：人民交通出版社，1996.

［7］ 邹毅松，王银辉.桥梁计算示例丛书 连续梁桥［M］.北京：［1］人民交通出版社，2009.

［8］ 乔建东，彭最.悬灌连续箱梁桥优化设计系统：中国，［1］2013SR072442［P］. 2013-03-26.

［9］He Meng, Chai Jun-rui. Two kinds of methods of mixing VB［1］and FORTRAN in one program and their comparison［J］.［1］Water Resources and Power，2005，23（1）：60-62.

［10］ Zhou Zhenhong，Wang Guobin，Bi Suping. Several ways to pass single string between Fortran and VB［J］. Journal of Zhengzhou University （Engineering Science）， 2011，32（1）：116-120.