利用移动最小二乘法进行点云变形分析的研究
吕志鹏,伍吉仓,2,郑二龙
(1.同济大学测绘与地理信息学院,上海 200092; 2.现代工程测量国家测绘地理信息局重点实验室,上海 200092)
利用移动最小二乘法进行点云变形分析的研究
吕志鹏1,伍吉仓1,2,郑二龙1
(1.同济大学测绘与地理信息学院,上海 200092; 2.现代工程测量国家测绘地理信息局
重点实验室,上海 200092)
三维激光扫描仪能够高精度快速翔实地获得变形体的空间信息,同时诸多变形体的变形情况也需要完整的描述和分析。为此,本文通过三维激光扫描仪获取变形体变形前后的点云数据,并利用移动最小二乘法进行均匀格网拟合内插来提取变形信息。通过模拟简支梁加载试验和上述方法进行变形分析,并与TS30高精度测量机器人的测量结果进行对比,结果表明两者精度相当,能够探测到毫米级变形。
三维激光扫描仪;点云;移动最小二乘法;变形分析;TS30
一、引 言
对各种建筑物、构筑物及山体滑坡等自然灾害频发区的变形监测是测绘领域的一项重要任务。从传统的大地测量技术到GNSS技术,变形监测的理论和方法已得到了广泛而深入的研究。然而,这些观测技术本质上属于基于点的测量方式,也就是说将变形体的变形特征用一些特征点进行离散化,然后通过测量这些特征点的空间位置变化来反演变形体的变形情况。它们的缺陷在于:一方面用有限的特征点反演变形体变形情况是否可靠仍值得商榷;另一方面由于对特征点的高度依赖性,一旦特征点被破坏将影响变形监测成果的连续性。三维激光扫描仪的出现则改变了传统变形监测作业模式,它是一种“面”测量设备,能够高精度、高分辨率、高效率地以非接触的方式获得变形体表面的点云数据,能够对变形体的变形情况进行全面的描述。利用三维激光扫描仪获取的点云数据进行变形分析已经取得了一些成果[1-7]。这些方法主要是利用点云数据拟合特征点、线来进行变形分析,应用范围具有局限性,不能达到对变形体的变形情况进行全面分析的目的。为此,本文利用移动最小二乘法拟合内插均匀格网来进行变形分析,以实现对变形体变形特征的整体把握。
二、移动最小二乘法
变形体空间变形中一类重要的情况就是沿着垂直方向的变形,分析该类变形需要根据点云数据拟合二维曲面,移动最小二乘法即可以利用不规则的空间数据建立连续的二维曲面函数[8-12]。因此,可利用移动最小二乘法进行点云数据的均匀格网拟合内插。对于三维激光扫描仪采集到的点云数据可以构造如下二维曲面函数,即
(1)
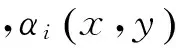
(2)
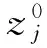
(3)
故有
(4)
其中
将式(4)代入式(1)可得
(5)

(6)
二维高斯函数图像如图1和图2所示,二维高斯函数满足上述权函数的紧支性要求。在图2中可以清晰地看到若干同心圆,并且同心圆所对应的函数值随其半径的增大而减小。同时,在同心圆外侧图像原色趋于深蓝色,其函数值趋近于0。
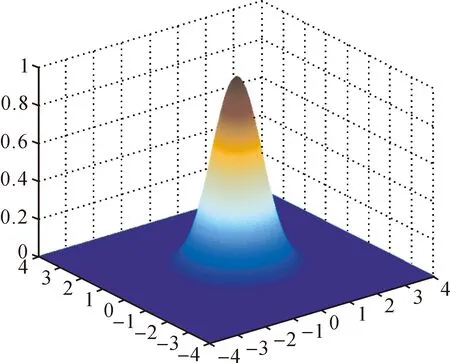
图1 二维高斯函数图像(h=1)
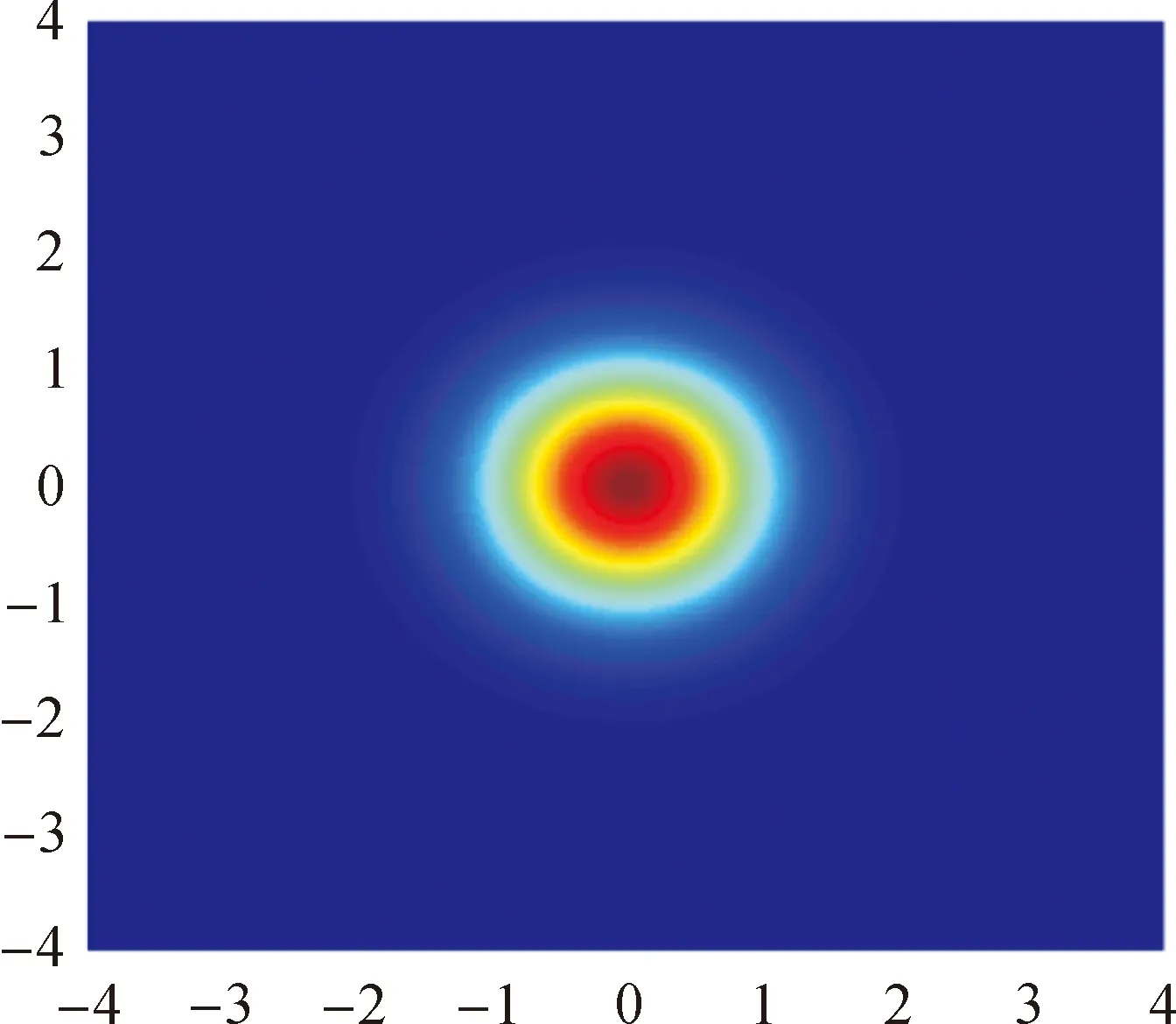
图2 二维高斯函数图像俯视图

应用移动最小二乘法进行点云变形分析的一般流程如下:
1) 将变形前后的点云覆盖范围在水平面上进行相同的格网化。
2) 对于变形前后点云的每个格网点有:①根据权函数的影响域确定拟合点集;②根据式(4)和式(5)计算格网点的函数值。
3) 将变形前后对应格网点的函数值相减获得变形量。
三、试验结果分析
本次试验通过不锈钢扁管(规格2200 mm×80 mm×30 mm)中部受压模拟简支梁的加载变形过程(如图3所示)。利用FARO Focus3D扫描仪在不锈钢扁管受压前后扫描其上顶面和正对扫描仪侧面的点云数据,扫描采用最高分辨率和最优扫描质量。同时在不锈钢扁管正对扫描仪侧面粘贴15个平面靶纸。在不锈钢扁管悬挂重物前后用Lecia TS30测量机器人(测角精度:0.5″,测距精度:0.6 mm+1×10-6D)测量15个平面靶纸的中心坐标,获取不锈钢扁管加载后的变形曲线。

图3 扁管中部受压试验
图3是不锈钢扁管中部受压试验实物图。不锈钢扁管中部1.8 m的范围(第一个到最后一个平面靶纸中心的距离)悬空。在试验过程中首先在空载条件下扫描点云数据,然后在0.90 m处悬挂重物再进行扫描。扫描前后提取的不锈钢扁管顶部点云如图4和图5所示。

图4 受压前扁管顶部点云

图5 受压后扁管顶部点云
在不锈钢扁管伸展方向的0、0.15 m、0.30 m、0.45 m、0.60 m、0.75 m、0.825 m、0.90 m、0.975 m、1.05 m、1.20 m、1.35 m、1.50 m、1.65 m、1.80 m处粘贴平面靶纸。在加载前后用TS30分别测量15个平面靶纸的中心坐标。测量过程中建立独立坐标系,坐标成果及变形量见表1。由表1可知,不锈钢扁管的变形基本呈现对称的特性,在加载点8号点处呈现出最大的变形量为15.5 mm,在两端变形量最小,约为1.7 mm。
在利用移动最小二乘法进行均匀格网内插时,需要将受压前后扁管顶部点云从仪器坐标系转换到变形体坐标系下。如图6所示,oxyz为仪器坐标系,o′x′y′z′为变形体坐标系。实际上可以认为仪器坐标系的z轴和变形体坐标系的z′轴指向相同。因而,两个坐标系之间变换可以简化为仪器坐标系绕着z轴的旋转和整体平移[15]。故有
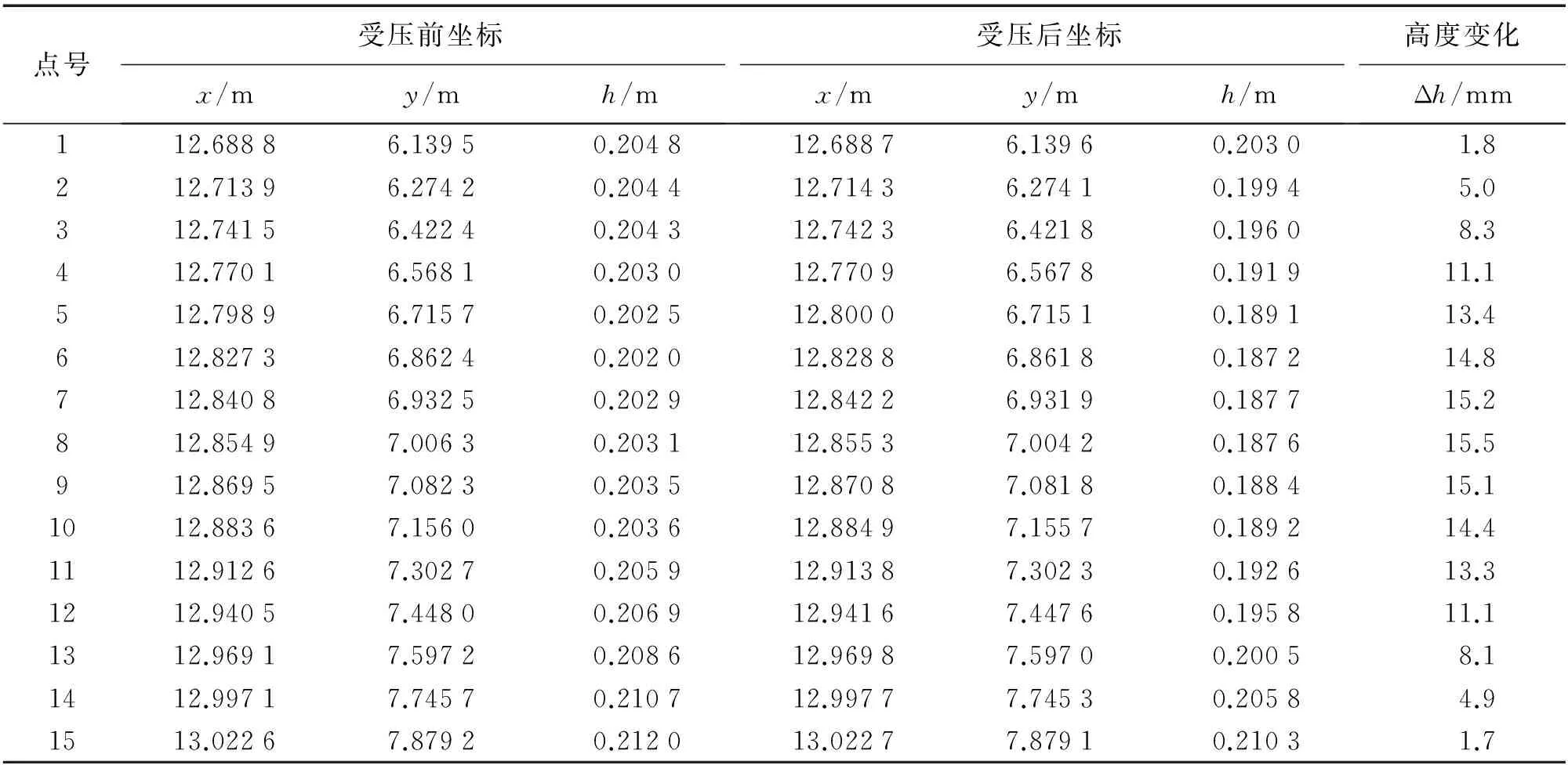
表1 扁管受压前后平面靶纸中心坐标及其变化
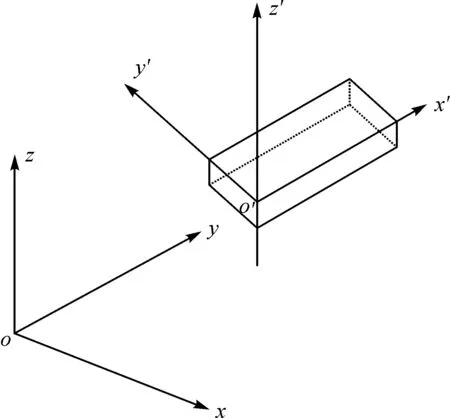
图6 仪器坐标系和变形体坐标系关系
(7)
式中,(x,y,z)为仪器坐标系下坐标;(x′,y′,z′)为变形体坐标系下的坐标;(x0,y0,z0)为变形体坐标系的原点在仪器坐标系下的坐标,其确定了3个平移参数;γ为仪器坐标系绕z轴的旋转角度。
提取出0和1.80 m处的平面靶纸的中心坐标,据此确定出仪器坐标系和变形体坐标系之间的旋转角度为-0.025 1 rad,然后根据0处的拟合中心坐标及已知平面靶标内圆的半径为0.015 m确定平移向量为(0.900 5, -1.139 4, 0.550 9)。据此将不锈钢扁管的顶部点云从仪器坐标系变换到变形体坐标系。
由上面的分析可知,不锈钢扁管顶面的有效点云范围是变形体坐标系x′o′y′面1.80 m×0.08 m范围内的点云。因此,首先将原始扁管顶部点云数据进行滤波降噪[16-17]并稀释,得到加载前的点云数为13 489个,加载后的点云个数为14 392个;其次将点云根据式(7)从仪器坐标系变换到变形体坐标系;然后分别沿x′轴和y′轴方向每隔0.005 m获得节点坐标形成均匀格网;最后用移动最小二乘法(式(6)中,h=0.005 m,采用1阶完备多项式)内插加载前后的均匀格网,按上节的方法获得扁管表面垂直向的变形量,如图7所示。

图7 内插均匀格网法变形图
由图7可知,不锈钢扁管在受压过程中整体上呈现对称的变形特征。在中间的变形量最大,约为15 mm,在两端的变形量最小,约为2 mm,这与TS30获得的变形数据相吻合。同时可以看到,图7中部区域呈现出微小的下深上浅特点,这与受压时扁管顶面前后受力不均匀有关。在变形图上边缘处存在明显的与整体不一致的变形趋势,主要是因为这部分点云质量不高,受到了扫描过程中边缘效应的影响,特别是在右侧上边缘尤其严重。从图3可以看出扁管后面偏右处是一黑色的椅子,激光束在扫描到扁管边缘时,一部分返回到扫描仪而另一部分照射到反射特性并不明显的椅子上造成较大边缘效应误差。
如图8所示,获取均匀格网在点(0, 0)、(0.15, 0)、(0.30, 0)、(0.45, 0)、(0.60, 0)、(0.75, 0)、(0.825, 0)、(0.90, 0)、(0.975, 0)、(1.05, 0)、(1.20, 0)、(1.35, 0)、(1.50, 0)、(1.65, 0)、(1.80, 0)处扁管在垂直方向的变形量,将其与TS30获得的平面靶纸中心z坐标变化进行比较,两者的变形趋势整体一致,最大互差为0.9 mm,互差的均方差为0.4 mm,说明两者具有良好的一致性。
四、结束语
三维激光扫描仪是一种“面”测量设备,能够高精度、高密度、高速度地获取变形体表面的空间信息,详细描述变形体表面细部特征。本文应用移动最小二乘法拟合内插均匀格网获取变形量并形成变形面,更加详细地描述了变形体的变形情况。同时,通过与TS30高精度测量机器人获取的变形结果进行比较发现,两种方法的变形量互差均方差仅为0.4 mm,具有良好的一致性。因而可以说,利用三维激光扫描仪探测毫米级变形具有可行性。三维激光扫描仪在高精度获取变形体的整体变形趋势方面应用前景广阔。
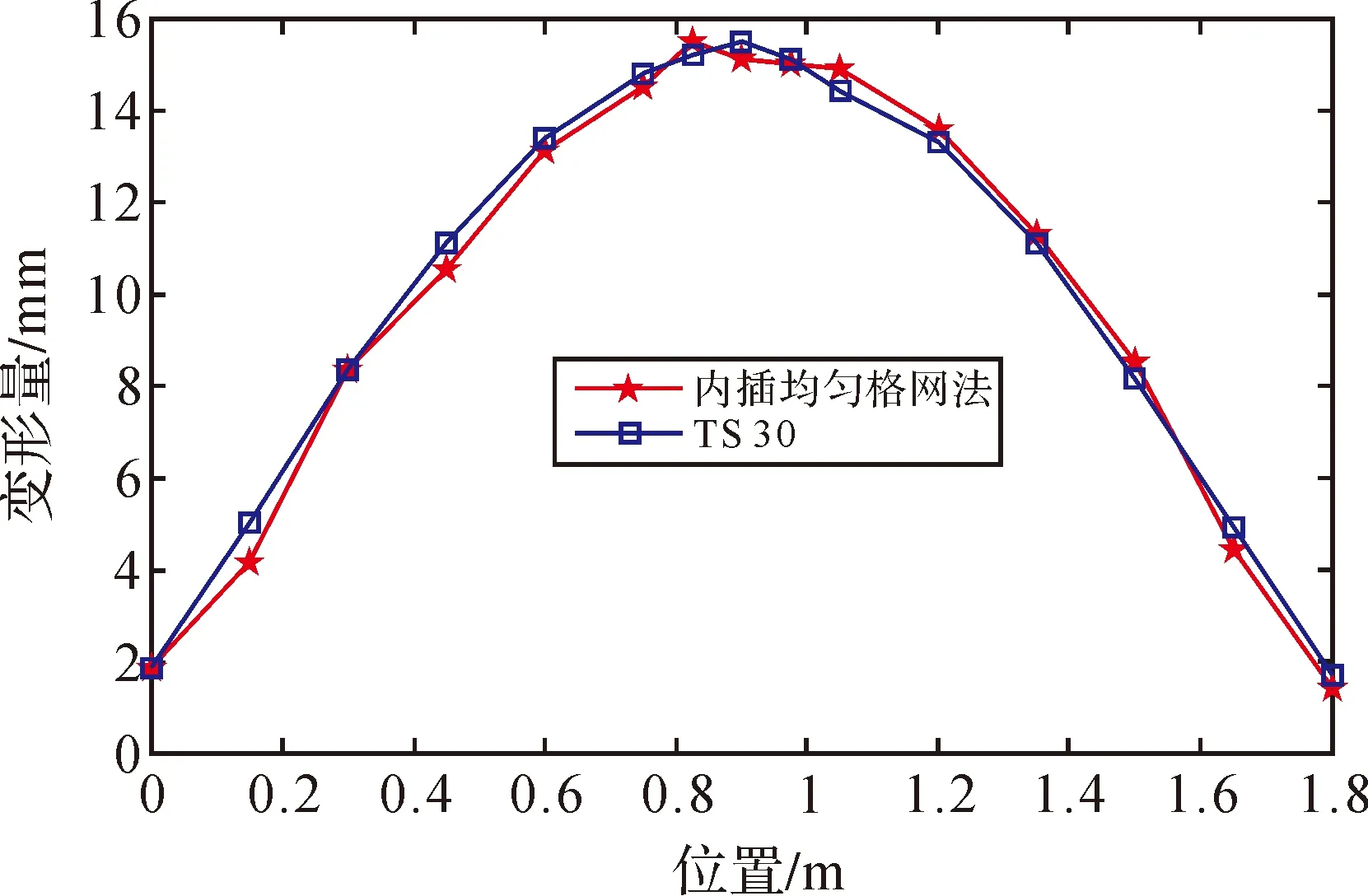
图8 变形量对比图
[1] 徐进军, 王海城, 罗喻真, 等.基于三维激光扫描的滑坡变形监测与数据处理[J].岩土力学, 2010, 31(7): 2188-2191.
[2] 戴华阳, 廉旭刚, 陈炎, 等.三维激光扫描技术在采动区房屋变形监测中的应用[J].测绘通报, 2011(11): 44-46.
[3] 王延亮, 夏国芳, 胡春梅.利用三维激光扫描技术进行工业设备三维重建及变形分析[J].测绘通报, 2012(2): 94-96.
[4] 黄晓阳, 栾元重, 闫勇, 等.基于三维激光扫描测量技术的井架变形观测[J].工程勘察, 2012, 40(4): 66-69.
[5] 刘云广.基于地面三维激光扫描的变形监测点分析[J].北京建筑工程学院学报, 2013, 29(2): 43-48.
[6] 吴侃, 黄承亮, 陈冉丽.三维激光扫描技术在建筑物变形监测的应用[J].辽宁工程技术大学学报:自然科学版, 2011, 30(2): 205-208.
[7] 毕俊, 冯琰, 顾星晔, 等.三维激光扫描技术在地铁隧道收敛变形监测中的应用研究[C]∥地理信息与物联网论坛暨江苏省测绘学会 2010 年学术年会论文集.南京:江苏省测绘学会,2010.
[8] LANCASTER P, SALKAUSKAS K.Surfaces Generated by Moving Least Squares Methods[J].Mathematics of Computation, 1981, 37(155): 141-158.
[9] MAISURADZE G G, THOMPSON D L, WAGNER A F, et al.Interpolating Moving Least-squares Methods forFitting Potential Energy Surfaces: Detailed Analysis of One-dimensional Applications[J].The Journal of Chemical Physics, 2003, 119(19): 10002-10014.
[10] SCHAEFER S, MCPHAIL T, WARREN J.Image Deformation Using Moving Least Squares[J].ACM Transactions on Graphics (TOG), 2006, 25(3): 533-540.
[11] AHN S H, YOO J, LEE B G, et al.3D Surface Reconstruction from Scattered Data Using Moving Least Square Method[C]∥ International Conference on Image Analysis and Processing.2005, 719-726.
[12] 曾清红, 卢德唐.基于移动最小二乘法的曲线曲面拟合[J].工程图学学报, 2004, 25(1): 84-89.
[13] LEVIN D.The Approximation Power of Moving Least-squares[J].Mathematics of Computation, 1998, 67(224): 1517-1531.
[14] PAULY M.Point Primitives for Interactive Modeling and Processing of 3D Geometry[M].[S.l.]: Hartung-Gorre, 2003.
[15] 施一民.现代大地控制测量[M].北京:测绘出版社,2003.
[16] TOMASI C, MANDUCHI R.Bilateral Filtering for Gray and Color Images[C]∥Sixth International Conference on Computer Vision.[S.l.]: IEEE, 1998: 839-846.
[17] FLEISHMAN S, DRORI I, COHEN-OR D.Bilateral Mesh Denoising[J].ACM Transactions on Graphics (TOG), 2003, 22(3): 950-953.
[18] 邓念武,朱杰兵.全站仪在隧洞三维变形监测中的应用研究[J].岩土力学,2003,24:158-161.
[19] 姜卫平,刘鸿飞,刘万科,等.西龙池上水库GPS变形监测系统研究及实现[J].武汉大学学报:信息科学版, 2012,37(8): 949-952.
On Point Cloud Deformation Analysis Using Moving Least Squares Method
LV Zhipeng,WU Jicang,ZHENG Erlong
吕志鹏,伍吉仓,郑二龙.利用移动最小二乘法进行点云变形分析的研究[J].测绘通报,2015(7):32-35.
10.13474/j.cnki.11-2246.2015.0205
2014-05-08
中美国际合作项目(2010DFB20190);国家自然科学基金(41074019)
吕志鹏(1988—),男,硕士生,主要研究方向为精密工程测量与变形监测。E-mail: lvzhipeng2007@gmail.com
P237
:B
:0494-0911(2015)07-0032-04

