焊缝收缩法焊接变形技术研究

徐 东， 李 兴， 李晓延， 张盈彬

(1.上海船舶工艺研究所， 上海200032； 2.北京工业大学， 北京100124)

焊缝收缩法焊接变形技术研究

徐 东1， 李 兴1， 李晓延2， 张盈彬1

(1.上海船舶工艺研究所， 上海200032； 2.北京工业大学， 北京100124)

以船体甲板结构为研究对象，采用热弹塑性法和局部整体法计算分析甲板分段典型焊接接头应变大小，并将该计算结果与实验测量结果相对比控制和验证有限元计算精准度。以典型焊接接头计算结果为基础，采用Weld-Planner焊缝收缩法预测甲板分段结构的焊接变形。采用焊缝收缩法计算工程结构的焊接变形时，计算过程易于收敛，计算效率显著提高，是预测大型复杂结构焊接变形一种方便有效的方法。

大型结构 焊接变形 焊缝收缩法 热弹塑性法 局部整体法

1 引言

现代造船中焊接工作量在整个船体建造总工作量中占相当大的比例，焊接水平的高低在很大程度上决定了船体的质量和生产效率，而焊接变形又是焊接过程中最难控制的一环。焊接过程不均匀的加热和冷却、材料的局部非协调塑性应变以及焊接残余应力的作用使得船舶结构产生各种焊接变形。焊接变形的存在不仅造成了焊接结构形状变异，尺寸精度下降和承载能力降低，而且在工作荷载作用下引起的附加弯矩和应力集中现象是船舶结构早期失效的主要原因，也是造成船舶结构疲劳强度降低的原因之一。

文章以船体甲板结构为研究对象，甲板结构由甲板板、纵横构架焊接而成。甲板多焊缝结构在焊接过程中不仅包含典型焊接接头存在的残余应力、失稳变形等问题[1]，同时多个焊缝结构之间存在内部作用力，易产生焊接变形。文中介绍以典型焊接接头计算[2～4]为基础的Weld-Planner焊缝收缩法[5，6]预测甲板分段结构的焊接变形。焊缝收缩法是基于焊接后焊缝部分的金属会发生收缩的原理而提出，焊缝在冷却过程中会发生收缩，这个收缩就是焊接残余应力和变形产生的原因。焊缝在收缩的同时在焊缝中产生等效收缩力和等效弯矩，通过等效收缩力和等效弯矩即可计算结果焊接变形，计算过程易于收敛，计算效率很高。

2 焊缝收缩法计算原理

进行工程结构整体焊接变形的计算方法之一是焊缝收缩法。焊缝收缩法是基于焊接后焊缝部分的金属会发生收缩的原理而提出，在实际应用中，可采用收缩力和收缩弯矩来实现焊缝收缩的计算。

焊缝在冷却过程中会发生收缩，这个收缩就是焊接残余应力和变形产生的原因。焊缝在收缩的同时在焊缝中产生等效收缩力，等效收缩力与收缩变形之间存在如下的关系：

式中：x为收缩变形量(mm)；K为等效收缩变形刚度(N/mm)；F为等效收缩力，(N)。

等效收缩力F可由焊接热输入的大小和材料的性能参数确定，通过如下的式子进行计算：

式中：E为材料的弹性模量(N/mm2)；q为焊接线能量(J/mm)；α为材料的热膨胀系数(℃-1)；c为材料的比热(J/kg℃)；ρ为材料的密度(kg/mm3)。

同样的，收缩弯矩是引起角变形的原因。等效收缩弯矩与角变形之间存在如下的关系：

式中：θ为角变形量(rad)；K0为等效弯曲变形刚度(N·mm)；M为等效弯矩(N·mm)。

图1所示为对接接头和T型接头中的等效收缩力和等效弯矩的示意图。焊缝收缩法采用的是线弹性的计算方法，不考虑焊接时加热过程和冷却过程的细节以及焊接冶金过程(相变)的变化细节，也不考虑温度变化对材料性能的影响，因此使用这种方法能够显著缩短计算时间。

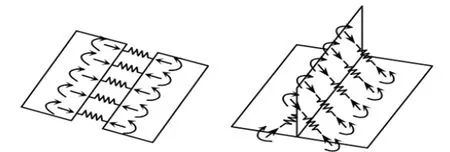
图1 对接接头和T型接头上的等效收缩力和等效弯矩

利用焊缝收缩法计算工程结构的焊接变形时，计算效率显著提高，计算过程易于收敛；并且利用焊缝收缩法计算时只需要材料在常温下的弹性模量和泊松比等弹性参数，这些参数都比较容易得到。由于焊缝收缩法进行了大量简化，并且没有考虑焊接加热及冷却过程，因此焊缝收缩法不能用于对焊接过程应力和变形的演化过程进行分析，这也是固有应变法、体积收缩法等计算方法都会遇到的问题。焊缝收缩法一般只适用于对大型结构焊接完成以后的残余变形进行计算，这个焊后残余变形的结果正是许多大型焊接结构所需要的。

3 典型焊接接头焊接变形试验

典型焊接接头焊接变形试验为甲板结构焊接变形计算做铺垫。在准确掌握典型焊接接头焊接变形规律的基础上，可以准确提取甲板结构焊缝的等效收缩力、等效弯矩等焊缝收缩法计算参数，保证甲板结构焊接变形预测计算的精度。

甲板结构焊接主要有甲板板面对接焊以及甲板板与纵横构架、纵横构架间角接焊，考虑到典型焊接接头焊接方法和焊接工艺的相似性，确定典型接头试验模型为两种，平位置对接焊试验模型和角接焊试验模型。平位置对接焊试验采用双面埋弧自动焊进行焊接，试验模型尺寸为长600mm×宽250mm×厚20mm；角接焊试验采用手工焊进行焊接，角接焊试验模型包含两种焊接接头：一种是水平位置角焊缝接头(平角焊接头)，另一种是竖直位置角焊缝接头(立角焊接头)，试验模型尺寸为底板长600mm×宽500mm×厚16mm，纵向腹板长600mm×高650mm×厚10mm，两块横向腹板宽245mm×高650mm×厚10mm。平位置对接焊及角接焊试验模型如图2所示，图2(a)为平位置对接焊，图2(b)为角接焊。

图2 典型焊接接头焊接变形试验

平位置对接焊板厚20mm，因此采用多层多道焊焊接，包含正面两道焊及反身碳刨(碳刨宽度14～15mm，深度7～8mm)后两道焊，平位置对接焊焊接工艺参数如表1所示。手工角焊平均电流150A，平均电压30V，平角焊接头平均焊接速度10.71cm/min，立角焊接头平均焊接速度5.23cm/min。

表1 平位置对接双面埋弧自动焊焊接工艺参数

平位置对接焊和角接焊试验过程中焊接变形测量点布置如图3所示，图3(a)为平位置对接焊测量点布置图，图3(b)为角接焊测量点布置图。

平位置对接焊试验实际测量焊接变形值如表2所示，角接焊试验实际测量焊接变形值如表3所示。其中长度值、宽度值解释：以L0105为例，L代表宽度，0105代表01、05测量点间的长度值；B0111，B代表宽度，0111代表01、11测量点间的宽度值。

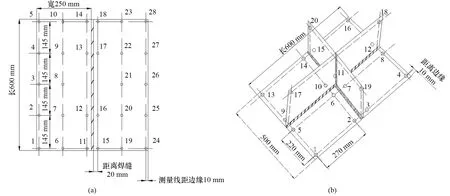
图3 典型焊接接头焊接变形试验变形测量点布置图

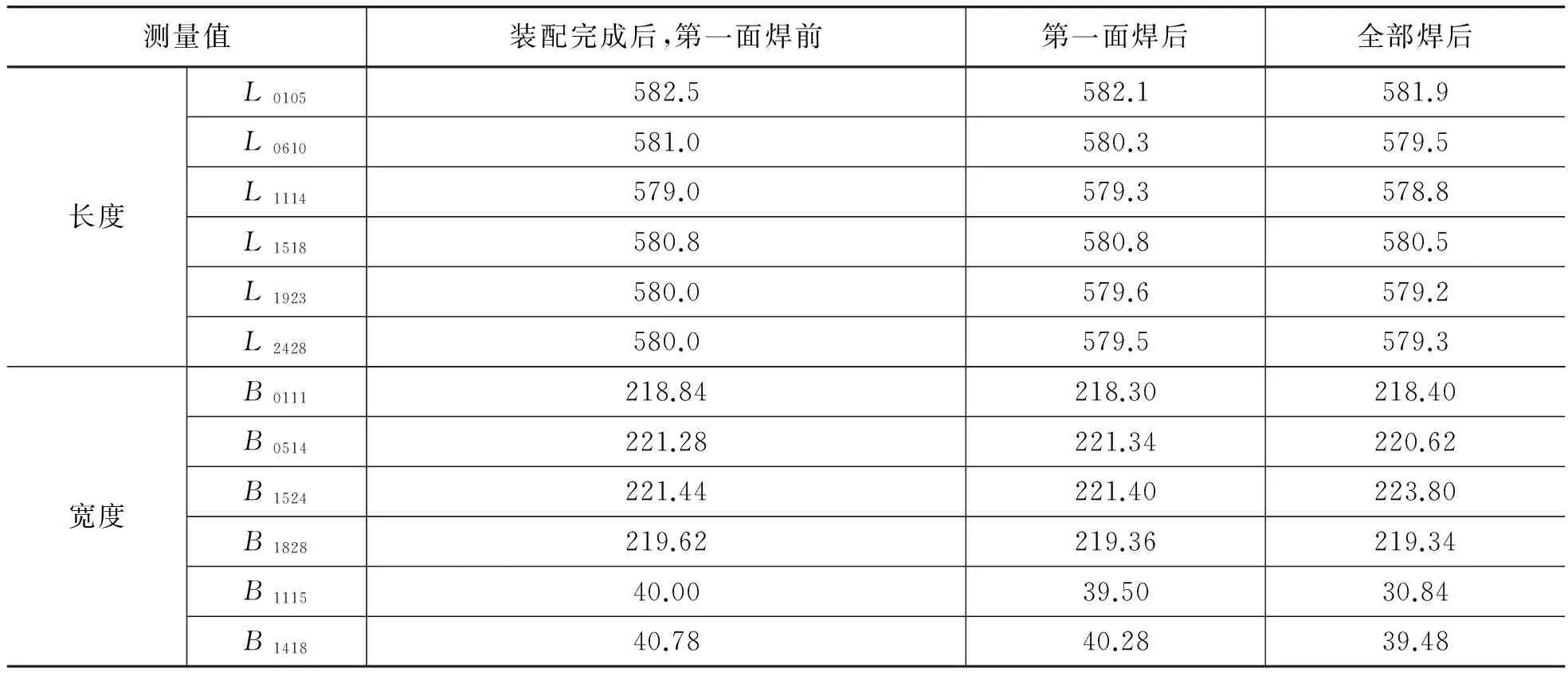
表2 平位置对接焊试验焊接变形值 单位：mm

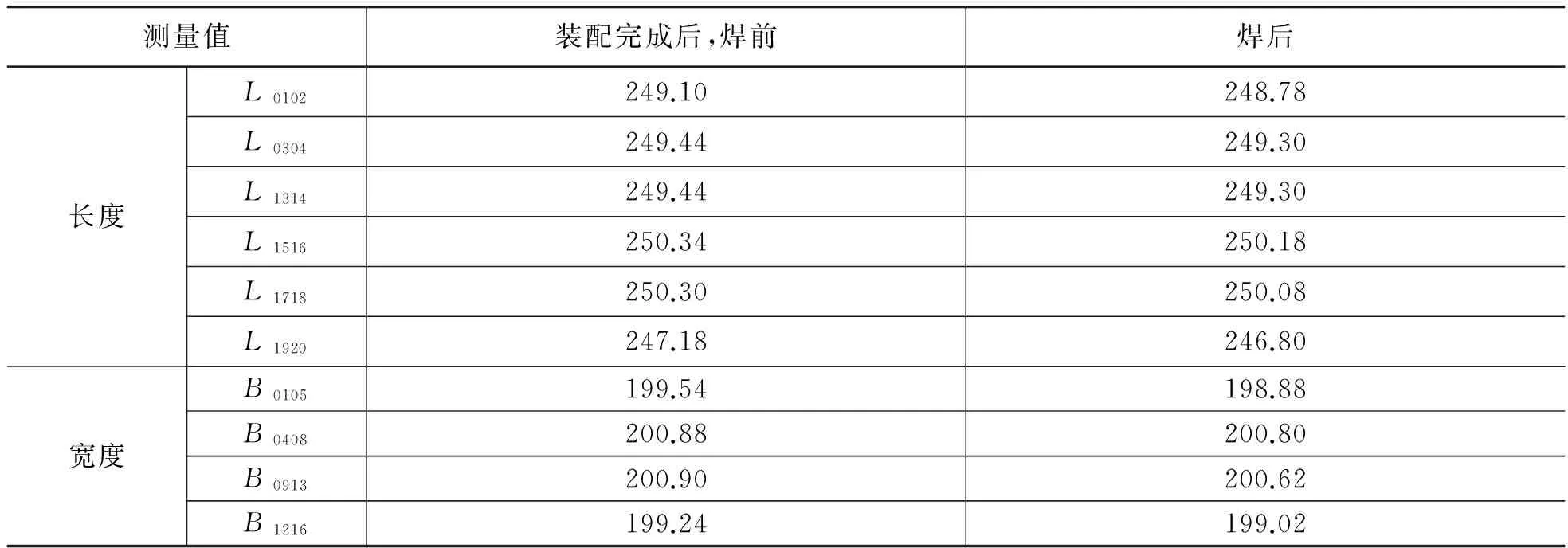
表3 角接焊试验焊接变形值 单位：mm

4 典型焊接接头有限元计算

平位置对接焊模型结构简单采用热弹塑性法进行计算，保证计算效率和计算精度；由于角接焊模型大，采用热弹塑性法进行计算网格数量庞大，计算效率低，因此采用局部-整体法进行计算。甲板分段采用的钢材材料参数如表4所示，其他计算条件及参数(如焊接电流、电压、焊接速度、层间温度等)均参照试验测量数据进行设置。

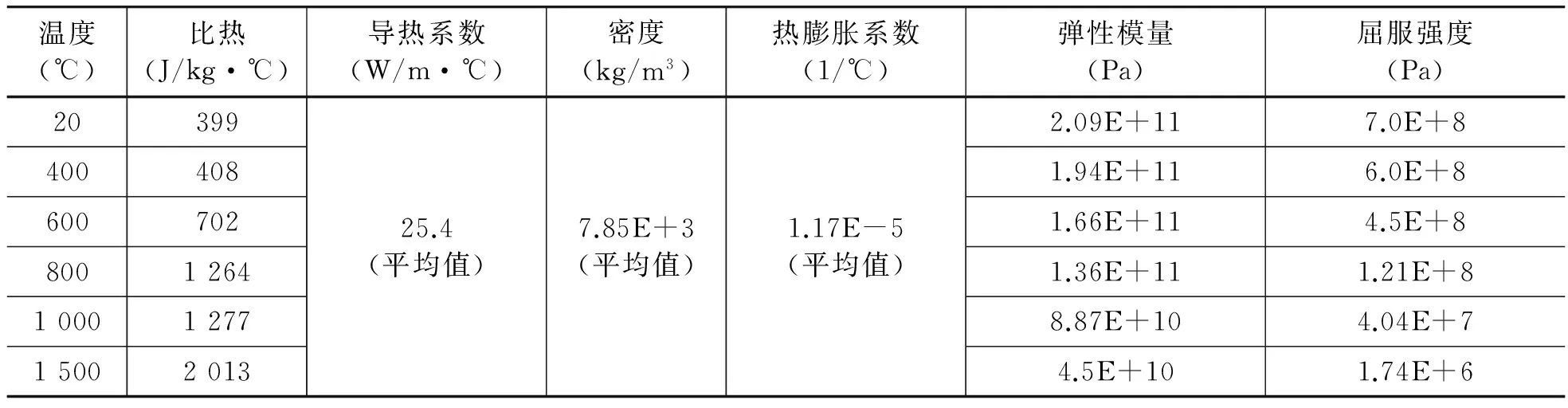
表4 钢材材料属性

4.1 平位置对接焊模型计算

平位置对接焊模型的焊接变形计算选用焊接专用数值计算软件SYSWELD，热源模型采用双椭球热源。图4所示为对接焊各道焊接时的熔池形貌，第二道焊前层间温度最高131.45℃，第三道焊前层间温度最高108.35℃，第四道焊前层间温度最高123.65℃，冷却后模型最高温度23.2℃。图5所示为对接焊各道焊结束后的模型变形情况。

图4 各道焊接的熔池形貌

图5 各道焊接结束后的焊接变形

由表2数据统计，平位置对接焊实测宽度方向最大收缩值(L0528和L0124)分别为2.24mm和0.64mm，均值为1.44mm；从有限元计算结果中提取相同位置的收缩值，为1.325mm。计算结果与试验结果对比，误差为

同理，最大纵向收缩值试验数据均值为0.68mm，有限元计算值为0.6625，误差为2.57%。

4.2 角接焊模型计算

角接焊模型焊缝较多，采用热弹塑性法计算对计算条件要求较高，计算效率低。这里采用局部-整体映射计算方法，即先利用热弹塑性方法计算出局部的T型和十字型焊接接头的变形，然后将计算得到的塑性应变结果提取出来导入到整体角焊接结构的模型上，进行弹性求解进而得出整体结构的焊接变形，计算软件采用PAM-ASSEMBLY。

有限元计算建模过程分别先建立局部模型、整体焊接SHELL模型，然后采用PAM-ASSEMBLY软件将局部模型向整体SHELL模型导入，实现结构焊接局部-整体映射，映射方向与实际焊接方向一致(红箭头方向)，如图6所示。将热弹塑性法计算得到的焊接变形值通过PAM-ASSEMBLY软件导入到整体角接焊模型，获得整体焊接模型结构的焊接变形大小，计算结果如图7所示。

图6 角接焊模型

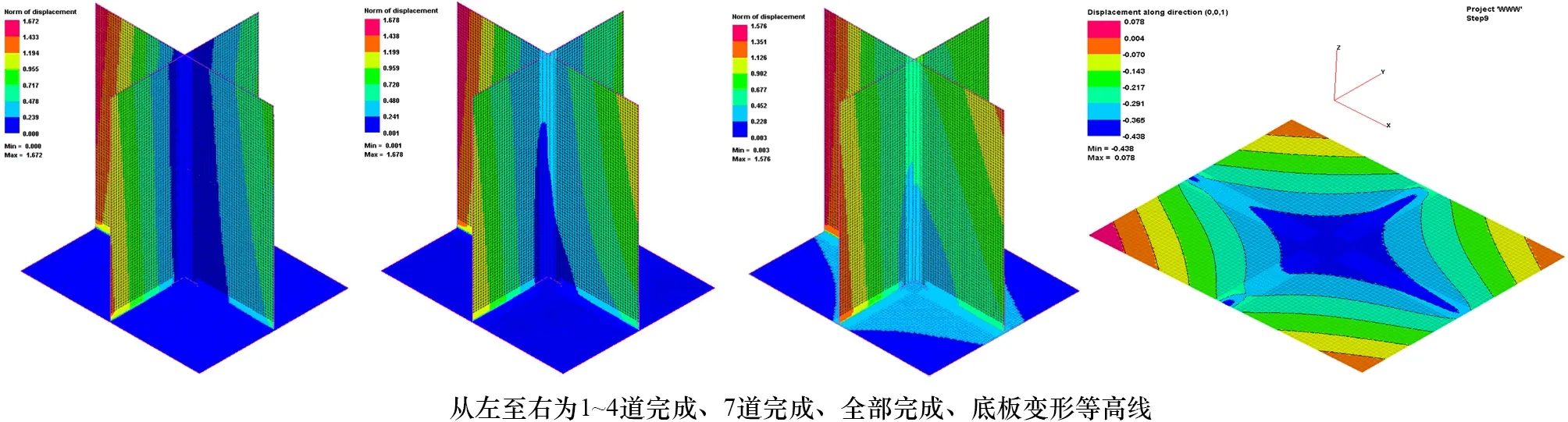
图7 角接焊变形计算结果

同上章节，对角接焊试验结果与有限元计算结果做对比，这里仅针对较关注的底板变形情况。最终结果为底板长度方向，试验测量收缩值为0.19mm，有限元计算收缩值为0.175mm，误差7.9%；底板宽度方向，试验测量收缩值0.31mm，有限元计算收缩值为0.280mm，误差9.7%。

从平位置对接焊和角接焊有限元计算结果与试验测量结果对比，验证了有限元计算的高精度，为后续甲板分段计算时等效收缩力、等效弯矩的计算和提取提供数据支撑。

5 甲板分段结构焊接变形计算

甲板分段结构的整体模型长21m，宽17.46m，甲板厚度为20mm，纵向构架和横向构架的围栏板厚10mm，扁钢尺寸为800×10mm，T型材尺寸16×550/20×250mm。甲板分段有限元模型如图8所示。甲板分段焊接采用的工艺参数与典型焊接接头采用的工艺参数相同，采用Weld-Planner焊缝收缩法进行计算，等效收缩力、等效弯矩根据典型焊接接头试验数据及有限元仿真计算提取。

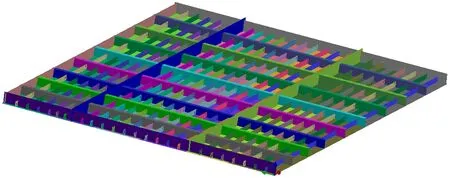
图8 甲板分段有限元模型

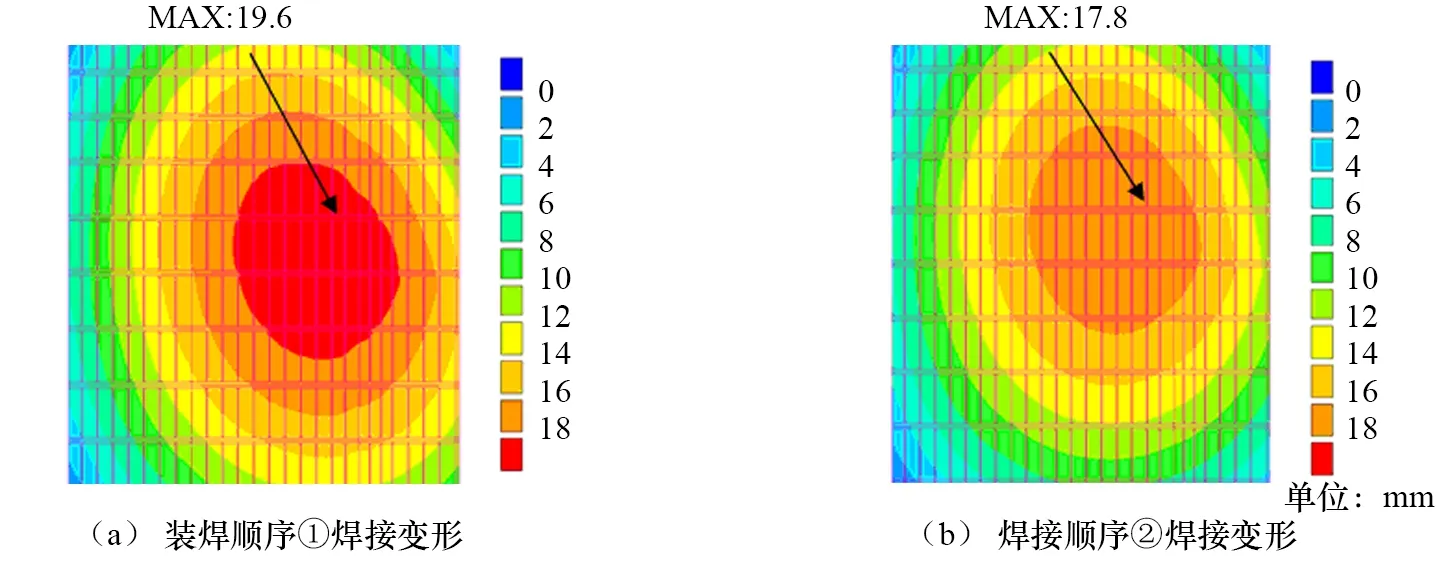
图9 两种装焊顺序结构焊接变形

甲板分段结构焊接变形计算过程中考虑了两种不同的装焊顺序：① 甲板拼焊对接焊缝→横向构架与甲板间角焊缝→纵向构架与甲板间角焊缝→纵向构架和横向构架之间的角焊缝焊接；② 甲板拼焊对接焊缝→纵向构架和横向构架之间的角焊缝→横向构架与甲板间角焊缝→纵向构架与甲板间角焊缝焊接。

两种装焊顺序的结果焊接变形如图9所示。从图中可以看出，第一种焊接顺序下结构的最大焊接变形量是19.6mm，第二种焊接顺序时结构的焊接变形量是17.8mm，比第一种焊接顺序时的变形量大约小9%。

上述焊接变形计算结果均与实际测量焊接变形数据(最大变形量15～20mm)相近。说明采用焊缝收缩法对于大型复杂结构计算的精度符合要求，可以为船体实际建造提高参考和依据。

6 结论

(1) 探讨了焊缝收缩法的计算原理，采用Weld-Planner建立甲板分段结构模型，进行焊缝收缩法焊接变形计算，计算精度较高。

(2) 分析了结构网格大小对计算结果的影响，当网格尺寸小于3mm×3mm时，计算得到的变形值是稳定的。网格尺寸小，计算精度高；为保证计算效率，细化焊缝附近网格，远离焊缝区域可逐渐加大网格尺寸，既保证计算效率，也可保证计算精度。

(3) 分析了不同装焊工艺对焊接变形的影响，计算表明甲板结构在焊接过程中先进行纵向构架与甲板的焊接，再进行横向构架与甲板的焊接，可以增加结构的刚性，所得最终的结构焊接变形要小一些。

[1] C.A.库兹米诺夫著，王承权译.船体结构的焊接变形[M]. 北京：国防工业出版社,1978.

[2] Y Vincent, F.B.J.B. Prediction of welding residual distortions of large structures using a local/global approach[J]. Journal of Mechanical Science and Technology, 2007，21: 1700-1706.

[3] X Fan, I.M.R.R.Simulation of distortion induced in assemblies by spot welding. Proceedings of the Institution of Mechanical Engineers, Part B[J].Journal of Engineering Manufacture, 2007: 1317-1327.

[4] Tsirkas S A, P.P.K.P. Evaluation of distortions in laser welded shipbuilding parts using local-global finite element approach[J].Science and Technology of Welding and Joining, 2003，2(8): 79-88.

[5] Mohd Shahar Sulaiman, Y.H.M.E. Simulation and experimental study on distortion of butt and T-joints using WELD PLANNER[J].Journal of Mechanical Science and Technology, 2011，10(25): 2641-2646.

[6] LU Yaohui, W.P.Z.J. Numerical simulation of welding distortion using shrinkage force approach and application[J].Advanced Materials Research, 2010，129/130/131: 867-871.

Research on the Calculation of Welding Distortion Based on Welding Shrinkage Method

XU Dong1, LI Xing1, LI Xiao-yan2， ZHANG Ying-bin1

(1.Shanghai shipbuilding Technology Research Institute, Shanghai 200032, China; 2.Beijing University of Technology, Beijing 100124, China)

This article focuses on hull deck structure and applies the thermal-elastic-plastic method and the local-global method to calculate the strain of welding joint in deck block, then compares the calculation results with experimental results to verify the accuracy of finite element calculations. Based on the calculation results of typical welding joint, the Weld-Planner shrinkage method is applied to predict the welding distortion of deck block structure. With this method, the calculation process of welding distortion in engineering structure is easy to converge and the calculation efficiency is significantly improved. It proves that this is a convenient and effective way to predict the welding distortion in large complex structure.

Large structure Welding distortion Welding shrinkage method Thermal-elastic-plastic method Local-global method

上海市博士后科研资助计划重点项目，项目编号：13R21420200。

徐 东(1976-)，男，工学博士。

U671

A