基于PSO算法的LNG水上泄漏扩散事故影响范围的定量计算

金全洲，齐奎利，曹蛟龙，程 康

(中国船级社 武汉规范研究所，武汉 430022)

基于PSO算法的LNG水上泄漏扩散事故影响范围的定量计算

金全洲，齐奎利，曹蛟龙，程 康

(中国船级社 武汉规范研究所，武汉 430022)

为提高LNG水上泄漏扩散事故影响范围定量计算的效率，采用粒子群优化(PSO)算法确定高斯模型中的扩散系数，构造一种简单的重气扩散模型，与利用挪威三维计算流体力学(CFD)软件FLACS计算的结果比较表明，两种方法在特定场景下的计算结果相当，本文方法更为简单。

液化天然气；泄漏扩散；计算流体力学；PSO

液化天然气(LNG)在储存、使用、运输过程中一旦发生泄漏会迅速气化扩散，如处置不当会造成火灾、爆炸危险性对人员产生伤害。扩散范围的大小会直接影响事故后果的危害程度，扩散计算是随后火灾、爆炸危险性计算的基础。近年来，国内外学者进行了大量的试验研究[1]，并综合采用了多种方法对LNG泄漏扩散的影响范围进行了定量计算。有学者推荐简单实用的BM模型，以重气扩散的实验测量数据为参考，用无因次形式将数据连线并绘制成与数据匹配的列线图，在一定程度上能体现重气扩散的情形[2]。箱及相似模型具有概念清晰、计算量较小等优点[3]。应用较为广泛的相似模型之一是美国海岸警卫队和气体研究院开发的DEGADIS模型[4-5]，此类模型对气云微元就动量平衡、质量评估、能量平衡进行分析，列出不同方向的动量守恒、质量守恒等控制方程，经过质量和能量交换后，气云逐步转化为湍流扩散，最终表现为一个纯粹的高斯分布[6]。该计算需假定速度和浓度的自相似分布，并且通常涉及不连续界面，具有很大的不确定性。基于纳维-斯托克斯方程组(N-S方程)的流体守恒定律模型[7]，具有最强的科学依据，可以提供最详细的关于LNG蒸气云在大气中流动和扩散的描述。但该方法计算耗时且代价高昂。综合上述进展，考虑利用挪威三维CFD软件FLACS的计算结果和公开发表的试验数据，通过PSO算法[8-9]对高斯模型中的扩散系数进行确定，提供一种简单的重气扩散计算方法，用以定量确定LNG水上泄漏扩散事故的影响范围。

1 高斯模型

高架连续点源高斯模型在无限空间连续点源高斯模型的基础上考虑地面对扩散的影响，模型表达式[10]为

(1)

式中:C——泄漏物质在空间任意点的浓度;x、y、z——下风向、垂直于下风向的水平方向,以及竖直高度方向上的空间位置;

Qm——质量泄漏速率；

σy——y向扩散系数；

σz——z向扩散系数;

u——风速；

H——泄漏点高度。

使用高斯模型进行计算的关键是扩散系数的确定。当泄漏介质的密度大于空气时，应对模型的扩散系数进行特别考虑，以反映重气扩散过程的特点。

2 粒子群优化算法

粒子群优化算法收敛速度快，没有很多参数需要调整，算法简单，广泛应用于函数优化、神经网络、模糊识别等多个领域。

PSO在解空间中初始化一群粒子(随机解)，然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪个体最优解和全局最优解对粒子群进行更新，更新过程按下式计算粒子群的速度和位置[9]。

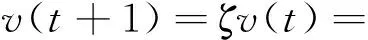
(2)

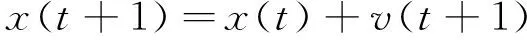
(3)

式中，v(t)——第代粒子群的速度;ζ——惯性因子，用以调节对解空间进行搜索的范围，较大时算法对解空间进行大范围搜索，反之则是小范围搜索;

c1、c2——学习因子，分别调节向个体最优和全局最优粒子方向风行的最大步长，若太小则粒子可能远离目标区域，若太大则会导致突然向目标区域飞去或飞过目标区域，合适的c1、c2可以加快收敛且不易陷入局部最优。

rand()——均匀分布在(0.1)间的随机数;

p(t)——粒子从初始到当前迭代次数搜索产生的个体最优解;

g(t)——粒子群目前的最优解,即全局最优解;

x(t)——第t代粒子群的位置。

为提高算法性能，对惯性因子ζ进行改进，使其能随进化代数自适应调节。设第t代飞行的惯性因子为ζ(t)，则有[11]

(4)

式中:ζini——初始值，本文取ζini=1; h,s——进化度因子和聚合度因子，分别表示为

(5)

其中:F[]——适应度求取函数；FT(t)——第t代所有粒子适应度平均值，可表示为

(6)

其中：d——初始化生成的粒子数目。

将式(5)、(6)代入式(4),使惯性因子随算法进行动态改变，使算法可以根据进化速度和分散度改变搜索空间，提高算法整体性能。

对算法的另一个改进是借用遗传算法中变异的概念，以一定的概率在粒子群中选择需要产生变异的粒子，变异粒子飞行方向不按照式(2)计算出的速度方向而是朝相反方向飞行。这样显著增加了种群在搜索过程中的多样性，是粒子群聚集度减轻，避免陷入局部最优解。

3 泄漏模型扩散系数的确定

扩散系数是泄漏点下风向距离的函数，同时受大气稳定度因素的影响。表1[10]给出了连续泄漏的扩散系数σy、σz随距离变化的函数关系。

表1 高斯连续泄漏扩散系数计算公式

由前所述，重气扩散过程经过质量和能量交换后，气云逐步转化为湍流扩散，最终表现为一个纯粹的高斯分布。另外，目前得到普遍认可的DEGADIS模型，其浓度在侧风向上采用高斯分布，在竖直方向上采用修正的高斯分布[12]，这在一定程度上使得用非重气扩散高斯模型预测LNG泄漏扩散成为可能，但需要对表1中的扩散系数进行重新确定。

(7)

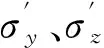
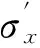
(8)

式中:Ai——待定系数,i=11,12,13。

将式(7)代入式(1)，并考虑式(8)，构造扩散模型：

(9)

构造优化目标函数FTA。

(10)

Ci——使用CFD方法计算确定的第个计算点的泄漏物浓度;

k——计算点个数。

使用PSO算法以式(10)为优化目标函数对Ai进行确定，代入(9)式得到重新构造的扩散模型。

4 算例分析

考虑宽阔水域的LNG泄漏场景，计算场景风速为5.7 m/s，LNG泄漏速度为30 kg/s，大气稳定度F。PSO算法参数设定见表2，计算确定的待定系数值见表3。

表2 PSO算法计算参数

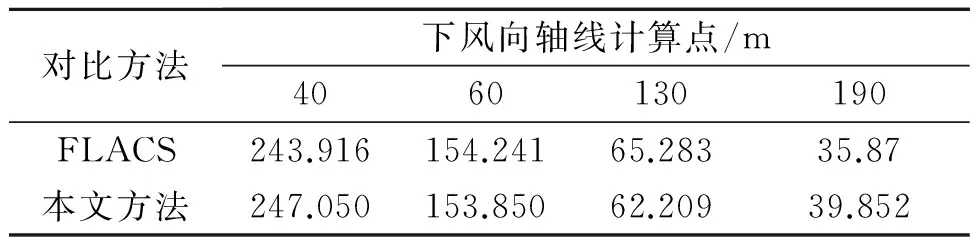
天然气可燃体积浓度范围为5%～15%，则气体浓度5%对应的范围为危险控制范围。图1为FLACS和(9)式计算得出的气体云团稳定状态下5%气体浓度范围，数值比较见表4。

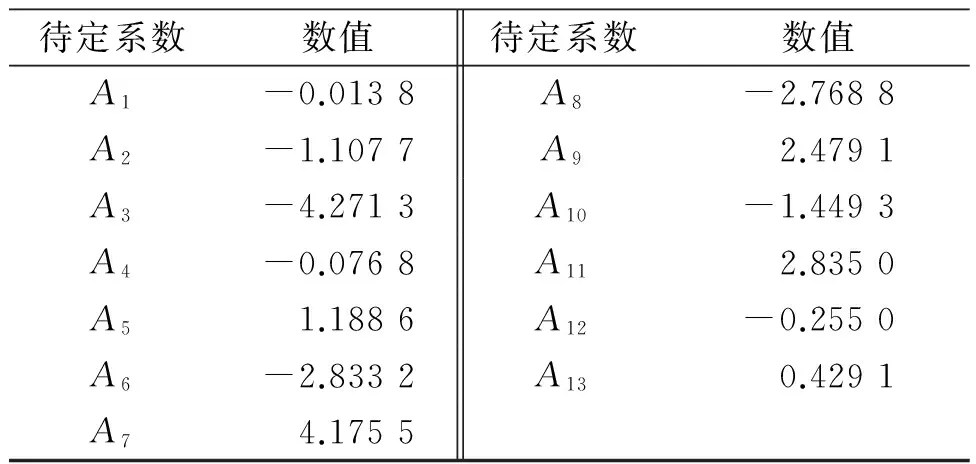
表3 待定系数计算值

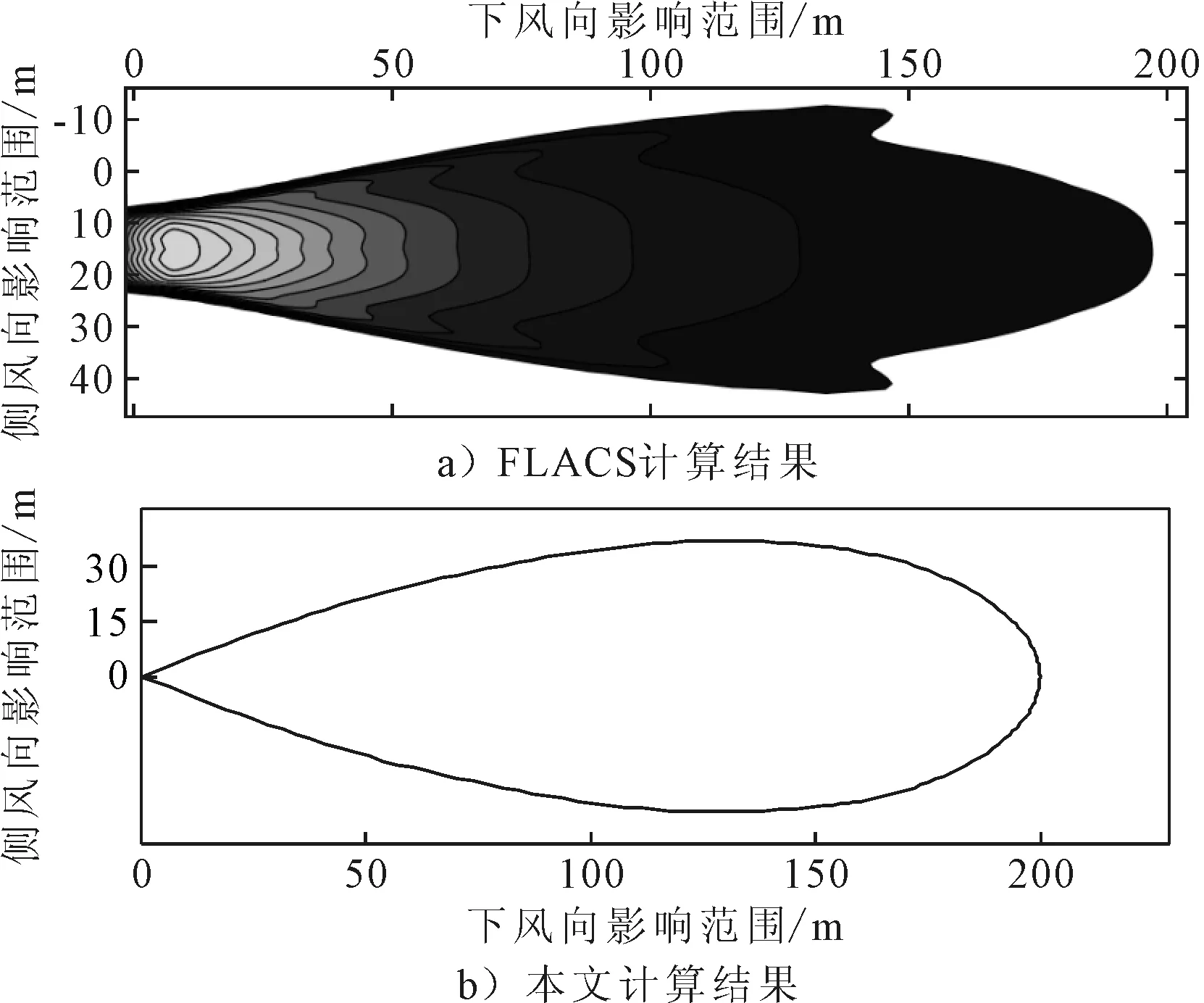
图1 稳定状态下的可燃气体范围(体积浓度5%)

5 结论

1)在对高斯连续泄漏模型的扩散系数进行重新构造和考虑下风向扩散系数的基础上，利用PSO算法可对LNG水上泄漏扩散行为进行计算。

2)在利用PSO算法搜索多参数最优解时，宜对惯性因子和粒子更新速度的更新方式进行改进，提高收敛速度的同时，避免陷入局部最优解。

3)本文算法仅适用于对LNG持续泄漏的稳定状态进行预测。对瞬态泄漏问题应在高斯瞬态泄漏模型的基础上进行考虑。无法对云团的时程扩散情况进行预测。

4)在不考虑障碍物的情况下，本算法对特定场景LNG水上泄漏的计算结果与CFD计算方法的结果相当。但本文算法方法简单，运算速度快，对典型场景进行充分计算并将修正后的扩散系数计算公式制表分类，可提高本算法的适用性。

[1] KOOPMAN,RONALD P E,DONALD L.Lessons learned from LNG safety research[J].Journal of Hazardous Materials,2007,140(3):412-428．

[2] BRITTER R E,McQUAID J．Workbook on the dispersion of dense gases[R]. HSE Contract Research Report,1988,No.17.Sheffield,U.K.1988.

[3] KUNSCH J P,WEBBER D M.Simple box model for dense-gas dispersion in a straight sloping channel[J].Journal of Hazardous Materials,2000,75(1):29-46.

[4] Van UlDEN,A P,A new bulk model for dense gas dispersion:two-dimensional spread in still air.In:Ooms G,Tennekes H (Eds)[C]∥Proc.IUTAM Symp.on Atmospheric Dispersion of Heavy Gases and Small Particles,1984.

[5] SPICER T O,HAVENS J A.Field test validation of the degadis model[J].Journal of Hazardous Materials,1987，16(0):231-245.

[6] 丁信伟，王淑兰，徐国庆.可燃及毒性气体扩散研究[J].化学工程，2000,28(1)：33-36.

[7] RICCIARDI L,PR VOST C,BOUILLOUX L.Experimental and numerical study of heavy gas dispersion in a ventilated room[J].Journal of Hazardous Materials,2008,152(2):493-505．

[8] KENNEDY J,EBERHART R.Particle Swarm Optimization[C]∥Proceedings of the 1995 IEEE International Conference on Neural Networks,1942-1948.

[9] 陈宝林.最优化理论与算法[M].北京：清华大学出版社，2005.

[10] 刘 茂.事故风险分析理论与方法[M].北京：北京大学出版社,2011.

[11] 金全洲.圆柱壳结构振动功率流主动控制研究[D].武汉：华中科技大学,2008.

[12] SUN B.Numerical simulation on dense gas dispersion and fire characteristics after liquefied natural gas release[D].Perth:Curtin University,2012.

Quantitative Calculation of Gas Dispersion after LNG Release on Water by PSO Method

JIN Quan-zhou, QI Kui-li, CAO Jiao-long, CHENG Kang

(Wuhan Rules and Research Institute of China Classification Society, Wuhan 430022, China)

In order to improve the quantitative calculation efficiency of gas dispersion after LNG release on water, the diffusion coefficient of Gaussian model is determined by using particle swarm optimization (PSO) method, and a simple dense gas dispersion model is developed. Comparing the numerical results of the model developed with those of a computational fluid dynamics (CFD) software FLACS, it is shown that the calculation results of the two methods are similar in particular scenes, while the method proposed is simpler.

liquefied natural gas; gas dispersion; computational fluid dynamics; PSO

10.3963/j.issn.1671-7953.2015.06.007

2015-08-24

金全洲(1980-)，男，博士，工程师

U674.13

A

1671-7953(2015)06-0027-04

修回日期：2015-09-22

研究方向:LNG水上应用

E-mail: qzjin@ccs.org.cn