基于遗传算法和贪婪算法的作业车间调度
王新, 贾志强, 尚宏美
(河北联合大学,河北唐山063009)
0 引言
进人21世纪以来,制造业生产模式随着科技的飞速发展和科技的进步在不断发生变化。快速多变且无法预测的买方市场由当初的大批量订购向着个性化、多样化方向转变,这就使得制造企业所面临的诸多问题比如社会环境、生产条件、物质供给等方面都发生了显著变化。因此,在这种情况下,一种以大批量生产的效益、提供满足客户个性化需求的产品和服务的定制生产方式应运而生[1]。由于生产车间有很多不确定因素,因此在生产调度问题上面临着巨大的挑战。过程规划和作业车间调度承担着巨大重任。过程规划的主要作用是完成对机器的分配过程,实现资源的优化配置;车间调度的工作是确定每台机器处理的工件和加工开始时间,为了完成所有进程并实现既定目标的优化。针对遗传算法的收敛速度不快、局部搜索能力差,生成最优解不精确等特点,本文提出一种新的算法基于遗传算法和贪婪算法的作业生产调度,它是在遗传算法原算法的基础上,引进贪婪变换进行个体解码来提高遗传算法在解的收敛速度和寻优能力。
1 基于混合遗传算法的车间调度问题
作业车间调度可以描述为1台机器加工N种工件(N是工件的集合),使用B种夹具以及C种刀具对工件进行加工(B是夹具的种类,C是刀具的种类),工件的总加工时间是T(T是所有工件加工用时间总和)。工件之间的操作序列,满足一定的约束。工件开始加工及加工工件前的准备工作是机器加工的第一个操作,工件在加工完成后都有它的特定的交货期,且不同工件的交货期不一样。当然在加工过程中使用的工具最少,步骤最精,工作时间最短,机器利用率最高这些都说明了生产调度性能最优[2]。本文主要研究一般性的Job Shop调度问题,在此问题满足以下特点[3]:
1)N为工件集,工件的种类记为K(K是所有工件细分后的种类),每个种类都有不同数目的工件,每个工件的操作步骤或许不相同但是步骤的顺序是固定的。
2)处理机器配有不同的处理工具,可以处理多种工件,工件加工时间来确定所需的约束,在处理计划中确保所有处理任务的完成。
3)每个工件有规定的到期时间,由于需要在规定的期限内完成工作任务,所以要求相同类工件的到期时间相同,方便机器统一加工;反之则不同。
4)在给定的时间内,1台机器只能够加工1个工件的1道工序,直到加工完此工序方可加工其他工序。满足以上四种条件的这种作业车间调度问题,都可以按工件交工延迟最短、机器加工最多工件、总加工时间达到最小为目的设计目标函数[4]。其目标函数为:

式(1)不仅考虑了操作工件所用总时间为最少,使工件的加工时间最集中、工具应用效率最高,还使得工件的加工量不会超出机器自身的承受能力,且保证了各工件完工期限的总延误最小。其中:i是工件号;j是工件加工的总天数计数;si是工件i的交工时间;Xi是工件i加工日的集合;wi是机器加工工件所用刀具数量的集合;ci是刀具加工工件工序的集合;v是机器在加工零件过程中的最大承受能力;ti是1台加工机器完成工件i操作加工的时间,它包括在加工工件不同工序时的机器等待时间,以及工件的安装时间和工件加工时间。
2 溶合遗传算法和贪婪算法
遗传算法是将自然进化论的理论应用到理论算法的一种随机搜索算法,它已成功地应用于作业车间调度,本文把贪婪变换G引入到遗传算法中,不仅能够发挥遗传算法在各种调度方案之间选择的优势,还能够弥补遗传算法的缺点,使得在调度方案中跳出局部最优的陷阱。
2.1 编码
编码的对象是工件,把每个工件看做对应的生物染色体,而个体的染色体的表示采用矩阵,m×n的矩阵Y=[yij]。i=1,2,…,m,j=1,2,…,n(m 为工件加工的天数,n 为工件的加工顺序)。一般来说,任何个体X,未必有X∈Ω(Ω是设计目标函数中的机器加工最多工件数)。于是引进贪婪变换(X)=Y=(y1,y2,…,yn)。若X∈Ω,则G(X)=X;若X∉R,则按照 ρi=ci/w(ixi=1)从小到大的次序变换xi=1到xi=0,一直到正好满足 为止,即得到G(X)=Y。显然X∈Ω是可行解。于是得到混合贪婪算法[5]的遗传算法,即在原来的遗传算法的搜索的各个步骤加上贪婪变换G。
2.2 初始种群的生成
编码成功以后,紧接着需要产生一个最优解[6],作为实际操作中整体的一个个体。
第一步:使矩阵(工件在任何一天中使用的夹具数记为bij)的所有元素bij记为0;
第二步:矩阵bij的列方向按降序排列,依次分析每个工件。
第三步:在第一行的工件,对于任何一个元素,完成相应时期的随机选择处理,然后执行下一个加工工件。
第四步:接着的加工工件需要在完工期限内进行加工,然后执行下一个工件的处理。
第五步:当所需加工工件的调度处理完成时,检查刀具、加工时间等条件是否满足,如果满足结束调度,否则返回第三步重新进行调度。
2.3 选择操作
对最优化作业车间调度问题的选择上主要依据是适应度计算。对于最小化问题,常见的适应度函数有F(X)=-f(x);F(X)=max(cmax-f(x),0);F(X)=1/(1+c+f(X)),(c+f(X)≥0)等。适应度决定了问题的最优化,也就是个体生存能力的最强选择。一般在最优化问题上会选择轮盘赌方式,按实际操作顺序(即个体Aj的适应度J(Aj))占整个操作顺序(即(种群)总适应度J(A)j)的比例划分整个赌盘,然后接着转动赌盘N次,在随机转动轮盘的过程中最好是能够转1圈以上,这样可以防止转盘不足1圈带来的概率不准确等缺点,最终选出赌盘的指针所指示的计数(个体)。即每次转动赌盘,选中Aj的概率J(A)j(A)j。在本文中按照适应度函数 (fX)=(fx1,…xn)=独立地从当前种群中选取M个母体。
2.4 交叉操作
基因重组是来自父代的提供的交配种群中的信息然后重新组合产生新的个体的过程。而每个个体都代表着不同的内容,他们在实际生产调度中都会有相应的约束,而在矩阵中代表工件不同操作顺序的某2个个体,让所有的操作顺序都并列而排出,选择任何一个交叉点实行交叉即上下交换操作顺序,代表个体的每个基因都以相同的概率Pc进行交换。
2.5 变异操作
变异就是按个体基因按小概率(变异概率Pm)扰动产生的变化,在变异过程中对整体矩阵实施贪婪变换G(Y(k+1))=(G(X1(k+1)),…,G(XN(k+1)))。实施贪婪变换的矩阵可以满足操作步骤、加工顺序等约束,但是可能不满足整个加工的完成期限的约束。因此,还要进行随机交换另外的个体产生新的子个体,直到满足完工期限的约束。
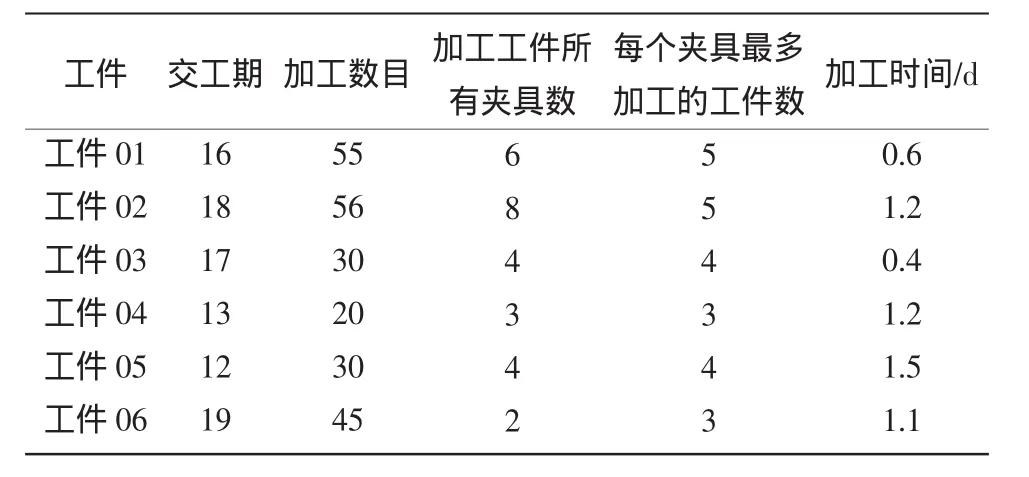
表1 某个月数据加工表
3 调度实例及模拟结果
现有如下调度问题:机器加工6个工件,其中在某月的加工计划数据表如表1所示。
在遗传算法中取个体的数目为90,交换概率Pc=0.98,变异概率Pm=0.02.群体经过400代的进化,算法收敛。得到6个工件调度结果的Gantt图(见图1)。经模拟计算,得到该问题的最佳调度如表2所示,同时可得群体中指标函数最小值为780。

表2 溶合贪婪变换的混合遗传算法下的最佳调度
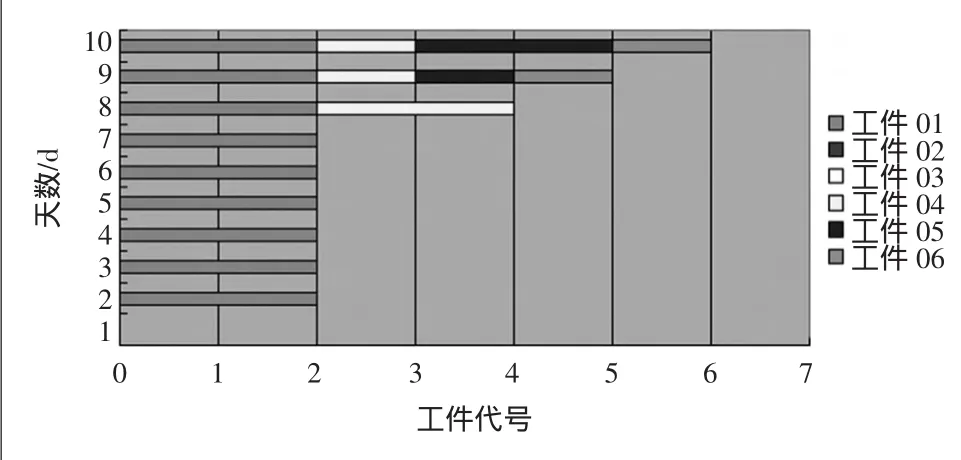
图1 甘特图
有了数据库中的数据,可以方便地根据这一数据生成基于工件的甘特图,图1中横轴表示工件代号,纵轴表示天数。从甘特图可以看出,工件在机器的加工上得到了合理的安排,既提高了机器的利用效率,又使得工件得以在最短时间加工完成。因此比较符合预期的结果。
4 结论
本文通过在遗传算法中引入贪婪变换,使得改进后的遗传算法在对作业车间调度问题求解上能够跳出局部最优的陷井,进而得到最适合的问题求解方法。将实际生产中的作业任务转化为染色体编码串,引进贪婪变换G,在原来遗传算法的选择、交叉、变异等步骤中加入贪婪变换,使得在解的质量和求解速度方面都有非常大的改进,从而给出了一个适合于生产调度问题求解的新算法。
[1] Bhote K R,Bhote A K.World Class Quality:Using Design of Experiments to Make It Happen[M].New York:AMACOM,2000.
[2] Cai Zixing,Gong Tao.Advance in research on immune algorithms[J].Control and Decision,2004,19(8):841-846.
[3] 曹金全,初红艳,费仁元.启发式算法和遗传算法在生产调度中的应用[J].中国机械工程,2006(增刊 2):211-214.
[4] 阳明盛,罗长童.最优化原理、方法及求解软件[M].北京:科学出版社,2006.
[5] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[6] 张文修,梁怡.遗传算法的数学基础[M].西安:西安交通大学出版社,2003.

