基于ANSYS的烧结炉卡箍拓扑优化

栗青， 孙博

（沈阳工业大学建筑工程学院，沈阳110870）

0 引言

随着近代化工工业的发展，压力容器在化工工业的作用也愈加重要。在传统的压力容器设计中，出于安全性的考虑，总是采用增加安全系数的方法来增大容器的安全性，在造成极大的浪费的同时也增加了制造成本与运输成本。并且在压力容器中应力分布并非均匀，在不连续的结构中，应力分布十分复杂，很多部分材料是多余的［1］。如何在保证安全性的前提下，降低成本，减少浪费成为设计者追求的目标之一。拓扑优化为达到这一目标提供了一种有效的手段。加工工艺的进步也为加工提供了保证。随着拓扑优化的发展，其在工业设计中逐渐受到重视，许多设计者也将关注点越来越多地集中到结构的拓扑优化上。通过对结构的拓扑优化，可以使整体结构在满足强度条件下，质量与体积大幅度减小，从而降低成本，减少浪费［2］。本文以烧结炉卡箍结构为例分析了压力容器部件，并进行拓扑优化，给出拓扑优化在结构中应用的基本方法。

1 理论推导

在通用的拓扑优化方法中，变密度法因为其精确性与较高的计算效率而受到广泛使用，变密度法所使用的拓扑变量是单元的相对密度。并根据单元相对密度的大小来决定单元的增减。借此，材料的性质的表达就可以通过密度与单元属性的函数关系来实现。弹性模量也可以通过变量的函数关系与相对密度联系起来［3］。

通过SIPM法，可以在体积约束的条件下，得到连续体的拓扑表达式［4］

式中：C为目标函数；xmin和xmax分别为取元相对密度的最大极限值和最小极限值；U为位移边界阵列；F为力向量；N为离散后单元的总数；V0、V分别为优化前后的体积；f=V0/V；K为优化前结构刚度矩阵；ve为优化后结构单元的体积；ue为单元位移列矢量；ke为单元刚度矩阵。

通过分析求解法可以得到，含有连续拓扑表达式约束条件和目标函数的拉格朗日函数［5］：

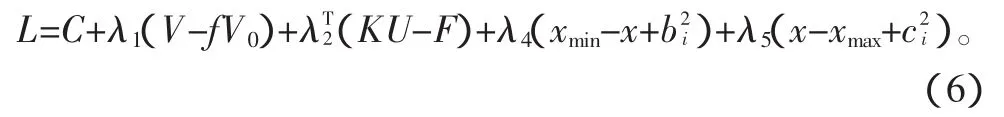
式中：λ1、λ2、λ4、λ5为拉格朗日乘子；xe是构成 x 的子向量；bi和ci是松弛系数。

当xe取极值时，拉格朗日的函数应该满足：

通过以上方法，经过不断地更新变量，便可以最终确定拓扑结构。

2 计算实例

2.1 工况参数

烧结炉卡箍模型的1/8模型如图1所示。卡箍内径R1=825.5 mm，内侧应力释放槽圆弧半径R2=15 mm，卡齿厚度S1=70mm，卡箍壁厚S2=89.5mm，卡槽宽度S3=101.5mm，内侧应力释放槽长度S4=60 mm，内侧应力释放槽圆弧宽度S5=16 mm，内侧应力释放槽深度H1=8 mm，齿面高度H2=30.5 mm，容器最高工作压力P=5.6 MPa（设计压力6 MPa），容器材料 16MnR，弹性模量 E=1.96×1011Pa，泊松比 μ=0.29，压力容器内径Dg=1 450 mm。

图1 烧结炉卡箍模型的1/8型

根据工况特性，选择轴对称力学模型进行分析。选择20节点Solid95进行网格划分，并进行分析。计算结果如图2所示。

图2 应力分布图

从分析结果可以得出结构中的最大应力Smax=438MPa。

2.2 优化参数设计

常用的分析软件进行拓扑优化的方法是变密度法。ANSYS也是基于这种理论进行分析。将模型材料的材料去除率设定为70%。计算结果见图3、图4。

图3 拓扑分析结果

图4 拓扑分析结果

分析结果可以看出。材料的主要密度的趋近于1的部分，全部分布在卡箍齿面的平行范围内，只有在齿面的部分以及在一对齿面中间部分是主要的受力部分。其他部分则可以适当简化。

2.3 优化设计

从以上的结构分析可以得出，原始设计中材料的利用率十分有限。在整个节点分布于需要简化部分的最大应力是5.8×107Pa，材料选用的是16MnR，其工作温度的许用峰值应力强度为598.2 MPa。有较大优化空间。在可以优化的部分中，主要载荷是拉应力。通过控制最大应力可知，减小30%最为合理。通过圆整，削减量是30 mm。

出于对加工方面以及安全性的考虑，削减范围不涉及卡齿以及其投影区域。载荷与边界条件同上。计算结果如图5、图6所示。

2.4 结果分析

优化后总体结构的应力分布如图5所示，从图中可以看出，在卡箍的总体结构中最危险处在齿面的边角处，经过削减的总体结构最大应力为458 MPa。与之前的最大应力438 MPa相比应力值略有增大，依然远远小于许用峰值应力598.2 MPa，但是总质量减小了大约18%。大大提升了经济性。

图6 优化设计后应力云图

3 结论

通过拓扑理论的分析与推导，找到了在可行域内寻求的优化设计方案，为今后的设计与优化提供了有力支持。

应用拓扑技术，有效地对卡箍的总体结构进行了分析。得到合理的分析结果，并设定了合理的优化方案。

从分析结果来看，通过拓扑优化，虽然整体结构的峰值应力有所增加，但是依然远远小于其许用应力，而且总质量减小了18%。在很大程度上降低了成本，使产品设计更为合理。

［1］ 杨姝.复杂机械结构拓扑优化若干问题研究［D］.大连：大连理工大学，2007.

［2］ 禹言芳，孟辉波.ANSYS在结构拓扑优化设计中的应用［J］.化工装备技术，2007（1）：56-58.

［3］ 夏天翔,姚卫星.连续体结构拓扑优化方法评述［J］.航空工程进展，2011，2（1）：1-11.

［4］ Rietz A.Sufficiency of a finite exponent in SIMP（power law）methods ［J］.Structural and Multidisciplinary 0ptimization，2001，21（1）：159-163.

［5］ 左孔天.连续体结构拓扑优化理论与应用研究［D］.武汉：华中科技大学，2004.

（编辑黄 荻）