火炮高低温压力曲线理论两个假设的数值分析

杜中华， 吴松

（军械工程学院，石家庄 050003）

0 引言

身管是火炮最基本的部件。火炮发射时，火药气体在身管内（身管尾部被炮闩封闭）燃烧，生成高温高压火药气体，推动弹丸高速飞出。发射过程中身管要承受很高的压力（实际上是压强，行业里习惯称之为压力），要确保身管不致破坏，身管必须具有一定的壁厚，但是壁厚过大，身管重量又会很大，故要根据身管每一截面发射时承受的最大压力来较准确地确定身管每一截面的壁厚。身管每一截面发射时承受的最大压力连接起来被称为身管设计压力曲线。目前确定身管设计压力曲线的主要方法是高低温压力法，所以习惯上把使用高低温压力法得到的身管设计压力曲线叫做高低温压力曲线。

高低温压力曲线是在内弹道平均膛压曲线和弹后压力呈二次分布曲线的基础上，假定弹后压力呈线性分布、将最大压力点位置人为向炮口方向前移1.5倍口径、假定高温情况下最大压力点对应弹丸行程变短等系列假设和人为干涉的基础上得到的，存在很大的近似，利用其设计身管壁厚必须加入安全系数［1-3］。本文采用数值计算方法研究了某型火炮的高低温压力曲线，对高低温压力曲线中的两个假设——弹后空间压力线性分布、高温下弹丸到达最大压力点的行程变短进行了分析，给出了去除这两个假设后更接近实际的高低温压力曲线（文中称为修正高低温压力曲线）。

1 经典高低温压力曲线理论

弹丸在身管内运动过程中，弹丸后部密闭空间（炮闩封闭身管一端）的平均压强p不断变化，压强p的变化规律通过求解内弹道方程组或者实际测试获得，其变化规律如图1所示。

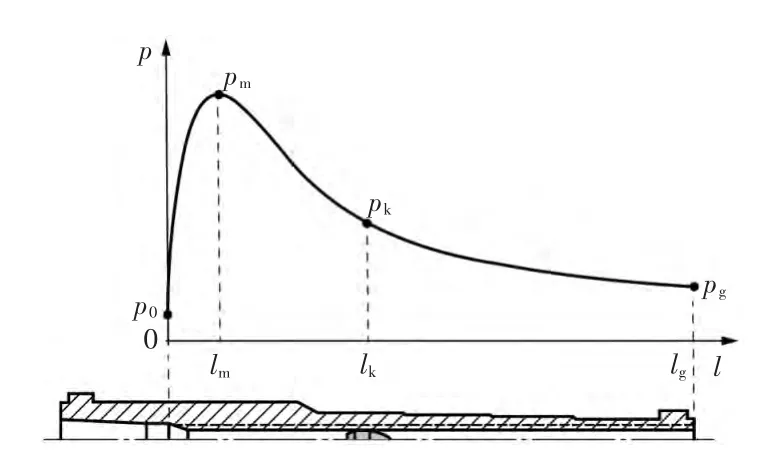
图1 弹后空间平均压力曲线

考查弹丸运动某一瞬间弹后空间的压强分布，各处压强分布并不均匀，弹丸底部压强pd小，膛底压力pt最大，分布情况呈现为二次曲线，表达式为

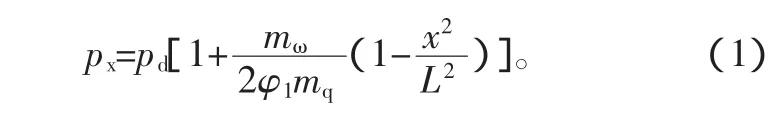
曲线如图2中实线所示。这里应注意的是，l表示弹丸行程，L表示弹丸底部距离身管尾端面的长度，两者相差一个药室长度。

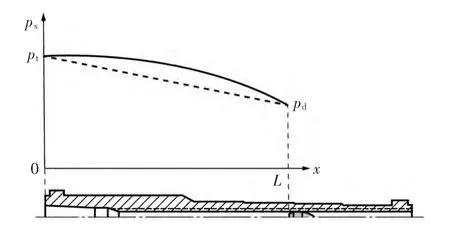
图2 弹后空间压力分布曲线

为简化起见，假定弹后空间压强为线性分布，如图2中虚线所示。综合考虑弹后平均压强不断变化以及弹后空间压强瞬间呈线性分布的特性，得到某温度下身管各截面承受最大压力曲线如图3所示。为安全起见，将最大压力点位置向炮口方向移动1.5倍身管口径距离。图中曲线由三段组成，（0，ptm）到（Lm+1.5d，pdm）间为直线，（Lm+1.5d，pdm）到（Lk，pdk）间为直线，（Lk，pdk）到（Lg，pdg）间为 pd～L曲线。可表述为“两直一曲”。

考虑到膛压随温度变化较大，故进一步考虑温度对膛压的影响，这里一般的假设是，温度升高，火药燃烧速度加快，最大压力增大，达到最大压力的时间缩短，弹丸行程减小；火药燃烧结束的时间提前，燃烧结束点弹丸行程也减小；由于火药气体膨胀充分，故在炮口位置压强变小。如图4所示。

图3 某温度下各截面最大压力曲线

图4 温度对膛压曲线的影响

将某一温度下各截面最大压力曲线和温度影响一并考虑，考虑极限温度50℃和-40℃下各截面最大压力，取外包络线即得到经典高低温压力曲线，如图5所示。高低温压力曲线通常包括4段，第一和第二段为直线，第三段为不同温度下的pdk组成的曲线，第四段为p-40d～L曲线。可表述为“两直两曲”［1-3］。

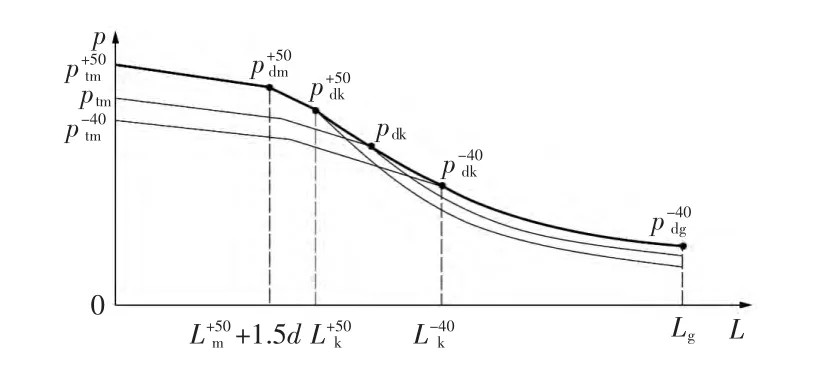
图5 高低温压力曲线

2 高低温压力曲线理论两个假设的数值分析

可以看出得到经典高低温压力曲线的过程用到许多假设，甚至人为的干预（将最大压力点位置向炮口方向移动1.5倍身管口径距离），这造成高低温压力曲线与实际情况可能存在较大差异。这里借助某型火炮身管高低温压力曲线的数值计算来分析其中两个假设［5］。

2.1 弹丸移动瞬间弹后压力呈线性分布

做线性分布的假设是为了计算方便，这是在计算机技术十分落后的时期，借助手工计算提出的假设。现在看来这个假设完全没有必要，借助计算机我们可以很方便地按照实际的二次曲线分布来处理，如式（1）所示。

按照线性分布假设，人为干预后，某温度下，“两直一曲”可以包络各截面压力变化，如图 6（a）所示。图 6（b）为最大压力点位置的局部放大图。

图6 线性分布假设及人为干预的外包络线

按照弹后压强二次曲线分布假设，人为干预后，某温度下，“两直一曲”不能包络各截面压强变化，尤其是身管后端面到最大压力点位置这一段，如图7（a）所示。图7（b）为最大压力点位置的局部放大图。

去掉人为干预的情况，直接取二次曲线分布假设下的外包络线，如图8所示（为分析外包络线各段组成，实际的外包络线没有画出）。则在身管后端面到最大压力点位置这一段，既包括最大压力点位置的弹后二次曲线，也包括最大压力点向炮口方向移动几个位置的弹后二次曲线，外包络线很复杂。但是借助计算机可以很方便地进行处理。计算机处理的外包络线如图9（a）所示。图9（b）为局部放大图。

2.2 高温下弹丸达到最大压力点的行程变短

装药温度升高后，由于火药燃烧速度变快，弹丸到达最大压力点的时间和燃烧结束点的时间均提前，这是没有问题的，如图10所示。但是药温增加后，弹丸运动速度加快，在某些火炮上，可能出现弹丸到达最大压力点的行程变长的情况，如图11所示。

图7 二次曲线分布假设及人为干预的外包络线

图8 二次曲线分布假设的外包络线

这样一来，极限温度下的“两直一曲”就如图12所示，按照经典理论处理的外包络线就如图13所示。不符合图5的理想状况，此时外包络线不能包络不同温度下各截面压强变化。要考虑到各种情况（高温下弹丸达到最大压力点的行程变短或变长）下各截面最大压力，外包络线直接用计算机处理即可。

2.3 对两个假设处理后的修正高低温压力曲线

去除2.1节的假设和人为干预，按照二次曲线分布用计算机处理极限温度下的各截面最大压力曲线如图14所示，其外包络线即为修正高低温压力曲线（为观察其各段组成，外包络线没有画出）。图14（a）为完整图，图14（b）和图14（c）为局部放大图。可以看出，修正高低温压力曲线的左端（身管尾端面一侧）为50℃下各截面最大压力，如图14（a）；右端（身管炮口一侧）为-40℃下各截面最大压力，如图14（b）所示；中间有一小段为15℃下各截面最大压力，如图14（c）所示。如果考虑多个温度，修正高低温压力曲线的中部组成将更为复杂，不过依旧可以用计算机处理。

图9 二次曲线分布及计算机处理的外包络线

图10 药温对p-t曲线的影响

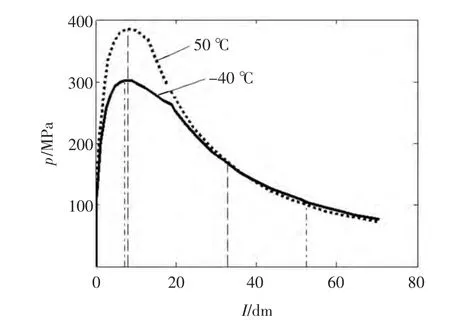
图11 药温对p-l曲线的影响

图12 不同温度下的“两直一曲”

图13 经典理论的外包络线

2.4 修正高低温压力曲线与经典高低温压力曲线的比较

将修正高低温压力曲线和经典高低温压力曲线对比如图15所示。同样，为分析成因，修正高低温压力曲线没有画出，想象为极限温度下各截面最大压力曲线的外包络线。图中实线为经典高低温压力曲线。图15中，（a）为完整图，（b）、（c）和（d）为局部放大图。可以看出相对经典高低温压力曲线，修正高低温压力曲线在身管尾端面附近变大，在身管中部偏小，在身管口部一段距离上变化不大。

应指出的是，内弹道学中关于内弹道平均膛压曲线和弹后压力呈二次分布曲线的相关公式也是建立在诸多假设基础上的［4］，消除这些假设要用到现代弹道学的知识，这里没有考虑。

3 结语

作为设计火炮身管壁厚的直接依据，经典高低温压力曲线理论采用了诸多假设，本文通过对某型火炮身管高低温压力曲线的实际计算，对两个经典假设进行了分析，在去除这两个假设和人工干预做法的基础上，借助计算机处理，得到了更接近实际情况的修正高低温压力曲线。本文的主要结论如下：

1）弹丸移动瞬间弹后压力呈线性分布的假设是手工计算时代的简化手段，可以借助计算机处理去除这个假设，同时去除将最大压力点位置向炮口方向移动1.5倍口径距离的人工干预做法。

2）高温下弹丸达到最大压力点的行程变短的假设对于一些火炮来说是不正确的，会导致经典高低温压力曲线不能包络各温度下各截面最大压力的情况，可以借助计算机处理，直接取外包络线，从而去除这个假设。

3）修正高低温压力曲线各段均为曲线，身管尾端面附近为50℃下各截面最大压力；身管口部附近为-40℃下各截面最大压力，中部组成十分复杂，要考虑不同温度下各截面最大压力曲线。

4）就某型火炮身管来看，修正高低温压力曲线相对于经典高低温压力曲线，在身管尾端面附近变大，在身管中部变小，在身管口部一段距离上变化不大。

图14 修正高低温压力曲线

图15 修正和经典高低温压力曲线对比

［1］ 张相炎，郑建国，扬军荣.火炮设计理论［M］.北京：北京理工大学出版社，2005.

［2］ 潘玉田.炮身设计［M］.北京：兵器工业出版社，2007.

［3］ 曾志银,张军岭,吴兴波.火炮身管强度设计理论［M］.北京：国防工业出版社，2004.

［4］ 金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2004.

［5］ 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用［M］.北京：清华大学出版社，2002.