曲柄摇杆机构的应用

马小军， 王继忠， 刘丹丹

（洛阳LYC轴承有限公司，河南 洛阳471039）

0 引言

在轴承摆动试验机构的设计中，要求能使内径为20～50 mm的向心球轴承在受纯径向载荷的条件下作摆动试验，摆动频率为0～200 min-1（可调节），摆角为0°～90°（可调节）。本文采用铰链四杆机构中的对心型曲柄摇杆机构来实现此摆动机构的设计。

曲柄摇杆机构是铰链四杆机构中最为常见的形式之一，而其中的对心型机构又因具有行程速比系数K=1的特征有特殊的应用意义。对心型曲柄摇杆机构有更多的限制，在传力性能方面也有自己的特点。

1 摆角90°时曲柄摇杆机构的设计

由于设计要求的最大摆角为90°，而摆角太大，相应最小传动角会很小。摇杆机构的传动角愈大对机构工作愈有利，通常使传动角γ≥40°。为了使传动角达到设计要求，在摇杆摆角为90°时，采用对心型曲柄摇杆机构。

1.1 各杆长的确定

图1所示为对心型曲柄摇杆机构。曲柄AB为原动件，摇杆摆角ψ=90°。该机构的几何特征是，当摇杆处于DC1、DC2两个极限位置时，铰链点C1、C2的连线通过回转中心A，故行程速比系数K=1。

取曲柄长度为a，其余各杆长度分别为b、c、d，如图1所示。按曲柄存在和对心型条件，各杆长应满足下列公式：

由图1可导出对心型曲柄摇杆机构中摇杆摆角ψ仅与曲柄长度a和摇杆长度c的比值有关，即

综上所述，各杆长可按下面步骤确定：1）选取曲柄长度 a=60 mm；2）选取机架长度 d=200 mm（d＞a）；3）取摇杆摆角 ψ=90°，按 ψ=2arcsin（a/c）求得 c=84.853 mm；4）根据c值，由式（3）知计算出 b＝190.788 mm。

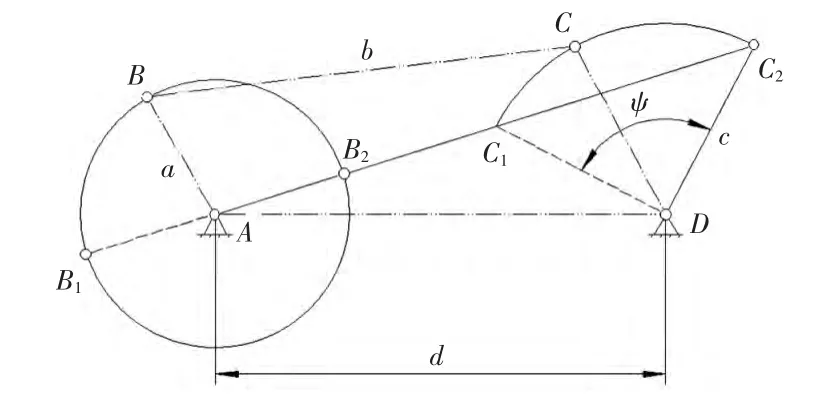
图1 对心型曲柄摇杆机构几何特征

1.2 最小传动角分析

当机构运转时，其传动角的大小是变化的，将机构运动循环中的最小传动角记作γmin，为了保证机构传动良好，通常使γmin≥40°。γmin必发生在曲柄与机架共线位置，如图2所示。由图2中的△B1C1D、△B2C2D几何关系和机构的对心型条件（3）可导出共线位置传动角γ1、γ2的计算式。推导的结果表明，γ1、γ2的计算式具有相同的形式：

由式（5）计算出 γ1=γ2=γmin=42.162°＞40°。

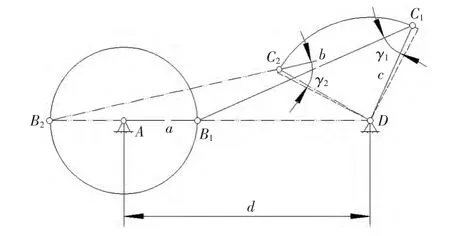
图2 对心型曲柄摇杆机构最小传动角分析

2 用图解法实现摇杆摆角的调整

在工程实践中，采用图解法是一种常用的设计方法。与解析法相比，图解法直观、速度快，但精度低。随着计算机技术的发展与计算机绘图的普及及应用，使得高精度快速的图解法设计成为现实。

如前所述，当摇杆摆角为90°时的对心型曲柄摇杆机构中摇杆摆角ψ仅与曲柄长度a和摇杆长度c的比值有关，有 ψ=2arcsin（a/c）。

现根据需要，摇杆摆角要从0°～90°可调节，在此采用了调节曲柄长度来达到调解摇杆摆角的目的。

现在电子图版下用图解法求摇杆摆角与曲柄长度关系。任取曲柄长度a′（a′＜a）,其余各杆的长度仍为b，c，d。如图3所示。作图如下：

1）以A点为圆心，以a′为半径作圆。

4）连接 DC1′、DC2′，则∠C1′DC2′即为曲柄长度为 a′时的摇杆摆角。

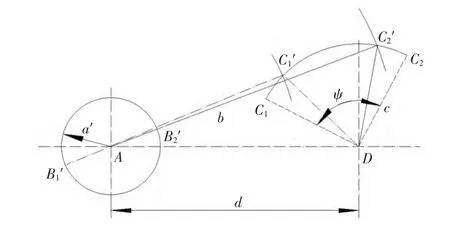
图3 摇杆摆角和曲柄半径关系

应当说明的是，此时的机构不是对心型曲柄摇杆机构，仅是曲柄摇杆机构。

3 结论

采用对心型曲柄摇杆机构可以实现试验机构的设计摆角，并可通过调整曲柄摇杆机构曲柄的长度来实现对摆角大小的控制。

［1］ 陈立德.机械设计基础［M］.北京：高等教育出版社，2004.

［2］ 邹蕙君，张春林，李杞仪.机械原理［M］.2版.北京：高等教育出版社，2006.

［3］ 杨世伟.曲柄摇杆机构设计的解释方法［J］.机械设计与制造，2006（4）：34-35.

［4］ 葛乐通.按行程速比系数设计曲柄摇杆机构的研究［J］.机械设计，2007，24（11）：40-42.

［5］ 张世民.机械原理［M］.北京：中央广播电视大学出版社，1983：89-100.

［6］ 成大先.机械设计手册［M］.北京：化学工业出版社，2002.

［7］ 侯慕英，汪平，田野.按许用传动角综合对心型曲柄摇杆机构［J］.机械设计，1997（2）：20-23.

［8］ 韦光华.按 γmin≥［γ］设计对心型曲柄摇杆机构的图表方法［J］.工程设计学报，2004，11（2）：96-98.

［9］ 卢治珍.对铰链四杆机构极位夹角定义问题的探讨［J］.机械设计与制造，2005(8)：86-87.

［10］ 孙桓，傅则绍.机械原理［M］.北京：高等教育出版社，1996.