直井受压管柱临界失稳长度有限元计算

张 强，安 超，丁宇奇，高 磊，蒋 豹

(东北石油大学机械科学与工程学院，黑龙江大庆 163318)

在钻井、完井、测井、压裂、采油等工程作业过程中，大量使用各种尺寸的管柱(包括钻柱、套管柱、测试管柱、抽油杆管柱、连续油管等)，分析管柱的屈曲行为，对于合理选择管柱尺寸和确定扶正器的安放位置等具有工程应用意义。

1744年，L.Eu1er对细长压杆的稳定性进行了研究，提出稳定性概念并得到了著名的欧拉公式;19世纪末20世纪初，S.P.Timoshenko提出了弹性稳定理论［1］;1962 年，Lubinski等［2］利用能量法对受压管柱在垂直井中的螺旋屈曲行为进行了研究，并首次提出了虚构力的概念;1977年，白家祉［3］提出了用纵横弯曲连续梁理论，求解井底钻具组合的受力和变形;1994年，高国华等［4］针对管柱在后屈曲进程中载荷与变形的关系，进行了更深入的研究，得到了管柱一、二次螺旋屈曲的临界载荷。随着计算机技术和仿真技术的不断进步，人们开始利用计算机进行仿真计算，其中最具代表性的要数ANSYS有限元计算软件，该软件提供了特征值分析方法来研究屈曲问题。

本文针对直井管柱临界失稳长度的计算进行研究，在现有能量法的基础上，采用特征值屈曲有限元法，利用ANSYS软件计算直井管柱的临界失稳长度，为工程应用提供理论依据。

1 能量法

假设管柱两端固支，其底部受轴向压力的屈曲形态如图1所示。在管柱由直线变成弯曲的过程中，管柱的弹性应变能增加了△U，同时由于底部轴向压力F的作用，引起管柱轴向位移的变化，而管柱所做的总功为△W，因此管柱总势能的增量为△Π =△U+△W。当作用在底部的轴向压力F较小时，管柱总势能增量为正值，此时管柱的直线平衡状态是稳定的。当作用在底部的轴向压力F超过某一数值时，管柱总势能增量变成负值，此时管柱的直线平衡状态是不稳定的。

图1 底部受轴向压力的管柱屈曲形态

当底部的轴向压力F达到临界载荷时，在微小扰动条件下，管柱总势能不变，即:

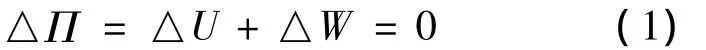
为了求得管柱的临界载荷，管柱偏离平衡位置后，假设满足两端边界位移约束的挠曲线函数为:

式中:x为管柱横向位移，m;y为管柱距上部固支处的轴向距离，m;A1为待定系数;L为管柱长度，m。

对式(2)进行一阶和二阶求导，得:

由于底部受轴向压力F的作用，引起管柱轴向位移的变化，底部轴向压力所做的总功为:

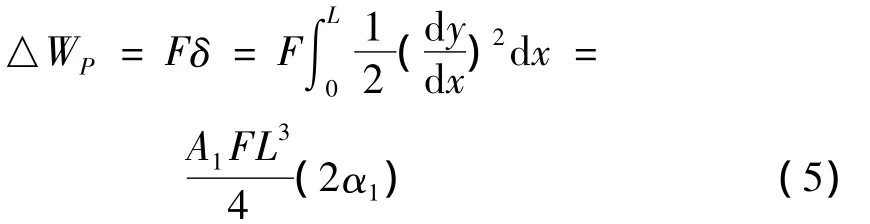
式中:F为管柱底部的轴向压力，N;δ为轴向位移，m;α1为系数。

在距离上部固支处的轴向距离y处，由于管柱自重的分布力，引起微小横向位移为δx，所做的功为:

式中:q为管柱自重引起的分布力，N/m。

管柱受压产生弯曲变形，增加的能量为:

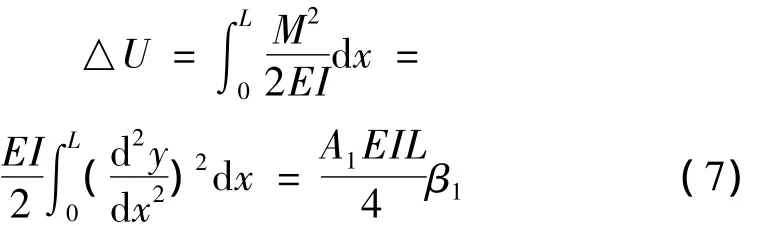
式中:E为管柱的弹性模量，GPa;I为管柱的横截面惯性矩，m4;M为弯矩，N·m;β1为系数。

将式(5)～(7)代入式(1)，便可求得使底部受压管柱保持稳定的临界失稳长度方程［5］:

式中:η为约束系数，其中两端为固支时取74.63，两端为铰支时取18.57。

2 特征值有限元法

管柱特征值屈曲分析是一种用于确定管柱结构开始变得不稳定时的临界载荷和屈曲构型的技术，其基于下列两个基本假设:1)管柱材料的应力应变关系是线性的，符合虎克定律;2)采用小位移。

分析管柱结构的稳定性时，管柱屈曲的临界载荷可表示为

式中:PQ为作用载荷，它包括管柱长度引起的自重载荷和底部施加的轴向压力;λ为管柱屈曲特征值因子。λ的计算公式为

式中:K为管柱的弹性刚度矩阵，即小位移的线性刚度矩阵;S为管柱的几何刚度矩阵，即初始应力刚度矩阵;ψ为特征位移向量。

特征值计算时要对所有的载荷作相应的缩放，但某些载荷是常数，如底部施加的轴向压力，而某些载荷是可变的，如管柱长度变化时自重也跟着变化。为了确保从常数载荷得到的刚度在特征值求解时不被缩放，需在特征解上迭代，调整可变载荷，也就是反复调整管柱的长度，直到特征值等于或接近于1.0，此时计算出来的管柱长度即为临界失稳长度。

3 临界失稳长度有限元计算

3.1 工程实例

某井采用尾管固井，尾管弹性模量为206GPa，长度为520.0m，外径为127.0mm，壁厚为9.19mm，浮重为182.2N/m，尾管在钻井液中的全部质量由井底支撑，假设扶正器为固支。

图2给出了两端固支管柱临界失稳长度随底部轴向压力的变化曲线，并与文献［5］中的结果进行比较。

图2 临界失稳长度随底部轴向压力变化曲线

由图2可见，底部轴向压力与临界失稳长度呈非线性递减关系。管柱靠近井底时，与文献［5］中的结果完全吻合，管柱离井底越远，与文献［5］中的结果偏差越大，且小于文献［5］中的结果。这是由于管柱远离井底时，相邻扶正器的底部轴向压力减小，导致对管柱屈曲的影响减小，扶正器的间距增加，导致管柱自重影响增大，使得相邻扶正器间的管柱挠曲线发生了变化，因而采用本文的有限元方法计算管柱临界失稳长度更合理。而文献［5］使用同一个挠曲线函数计算不同轴向压力情况下的管柱临界失稳长度，与实际情况存在一定的偏差。

3.2 无量纲临界失稳长度

令管柱长度系数m=(EI/q)1/3，则管柱长度L、每一个失稳段底部的轴向压力Fd和临界失稳长度Lcr可表示为

式中:ζ是管柱无量纲长度;γ是管柱无量纲临界失稳长度。文献［6］和［7］将无量纲临界载荷分别写成 Q= γ3，k= γ3。

两端固支是指在扶正器支承处有弯矩无转角，两端铰支是指在扶正器支承处有转角无弯矩。显然，井眼内的管柱变形在扶正器支承处转角非常有限，而弯矩随管柱变形的增大而增大，因而管柱在扶正器支承处，既不是固支，也不是铰支，而是介于固支和铰支之间且以固支为主的一种约束状态［5］。

图3 临界失稳长度随底部轴向压力的无量纲变化曲线

在两端固支和铰支条件下，图3给出了无量纲临界失稳长度随底部无量纲压力载荷的变化曲线，由图可见，两种约束条件对管柱临界失稳长度影响较大，无量纲临界失稳长度随着底部轴向压力的增加而逐渐减小。工程应用中，管柱无量纲临界失稳长度应介于固支临界失稳长度和铰支临界失稳长度之间，且应更接近于两端固支临界失稳长度。得出无量纲临界失稳长度后，利用式(12)，便可求出管柱的临界失稳长度值。

4 结束语

本文采用特征值屈曲的有限元法，计算得出的管柱临界失稳长度更合理，可用于石油行业中井下各种直井受压管柱的临界失稳长度分析，对扶正器合理安放间距具有一定的指导意义。

本文研究的管柱线性屈曲问题，处于管柱屈曲的初始阶段，今后可考虑在管柱受井壁约束的条件下，采用特定的有限元法，进行直井有重管柱非线性后屈曲研究，分析计算管柱正弦屈曲和螺旋屈曲的临界失稳长度及其临界载荷。

［1］ Timoshenko S P.弹性稳定理论［M］.北京:科学出版社，1965.

［2］ Lubinski A，Althouse W S，Logan JL.Helical buckling of tubing sealed in packers［J］.Journal of Petroleum Technology，1962，14(6):655－670.

［3］ 白家祉.应用纵横弯曲连续梁理论求解钻具组合的受力与变形［C］//国际石油工程会议论文集.北京:石油出版社，1982:67－69.

［4］ 高国华，李琪，张建仁.管柱在垂直井眼中的屈曲分析［J］.西安石油学院学报，1996，11(1):33－35.

［5］ 覃成锦，徐秉业，高德利.垂直井中管杆柱的扶正器安放问题研究［J］.石油钻采工艺，2000，22(3):8－12.

［6］ 刘洋，杨永波，梁枢平.轴向均布载荷下压杆稳定问题的DQ解［J］.力学与实践，2005，27(2):44－47.

［7］ 李清禄，李世荣.受均布载荷压杆后屈曲形态的数值计算［J］.力学与实践，2010，32(3):41－43.