基于动量BP神经网络的混沌系统同步与保密通信研究

杨文光，綦 涛，高艳辉

(华北科技学院基础部，北京东燕郊 101601)

0引言

混沌是一种貌似无规则的运动，指在确定性非线性系统中，不需附加任何随机因素亦可出现类似随机的行为(内在随机性)。混沌系统的最大特点就在于系统的演化对初始条件十分敏感，因此从长期意义上讲，系统的未来行为是不可预测的。混沌科学是随着现代科学技术的迅猛发展，尤其是在计算机技术的出现和普遍应用的基础上发展起来的新兴交叉学科，近年来，混沌在通信、社会科学、经济科学、自然科学、生命科学等各个领域得到广泛应用，并引起了人们的兴趣。在非线性电路中混沌信号的一个显著特性是它的非渐近稳定。一个完全相同的自治混沌系统，当系统的初始条件有一微小差异时，系统的运动轨道在同一相空间将会变得毫不相关。因此，有人认为混沌系统似乎是难以同步的。但是，1990年Pecora和Carroll发现一个混沌系统的某些相同的子系统在特定的条件下可以相互同步。这里的两个系统的同步，是指一个系统的轨道收敛于另一个系统轨道的同一值，它们之间始终保持步调一致，并且这种同步是结构稳定的。至此混沌系统被广泛地应用于保信通信中［1－7］。混沌保密通信是在发射端将信息埋入发射系统的混沌信号中，接收端接收含有信息的混沌信号并提取出信息。混沌保密通信需要发射端(驱动系统)与接收端(响应系统)两混沌系统的同步。

近年来，随着研究的不断深入，人们先后提出一系列有效的混沌同步控制方法，例如，耦合同步，连续变量反馈同步，自适应控制同步等［4－8］。混沌遮掩始终是最为经典和常用的一种，以其易于实现而深得人们的青睐。考虑到多层前向神经网络，具有以任意精度逼近任意非线性连续函数的能力，所以神经网络具有较强的处理不确定性和外界干扰的能力，因此被广泛用于控制领域。鉴于多层神经网络的复杂性，为了实现上的便利性，本文选用仅含单一隐含层的BP神经网络，相关文献已经证明它能够以任意精度逼近任意的连续函数。本文设计一种神经网络控制器来实现混沌系统的同步。首先设计出n个误差输入函数，然后分别以这n个函数为输入设计一个含有n个单输入单输出的神经网络模型，神经网络的输出即为控制器的控制量。最后通过仿真实验对该同步方法进行了验证，并结合保密通信验证了其具有良好的保密性能。

1 混沌同步系统的描叙与控制

选择驱动系统的数学描述为:

其中 x=(x1，x2，…，xn)T∈Rn为状态向量，A∈Rn×n为常数矩阵，f(x)为非线性连续函数。

选择响应系统的数学描述为:

其中 y=(y1，y2，…，yn)T∈Rn为状态向量，u(t)=(u1(t)，u2(t)，…，un(t))T∈Rn，f(y)为非线性连续函数。控制的目标是设计合理的控制器u(t)，使得响应系统能够渐近跟踪驱动系统，并最终实现同步，即

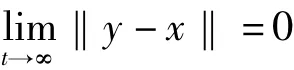
定义误差 e=y－x，e=(e1，e2，…，en)T∈Rn，由公式(1)与(2)可得误差系统为

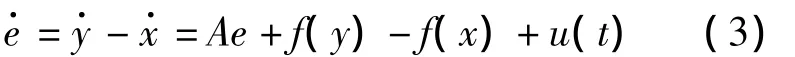
根据神经网络的万能逼近原理，任何一个连续的非线性函数都可以通过理想权值的神经网络来以任意精度逼近。我们的目标是充分利用神经网络的在线学习能来设计一组控制器u(t)使得根据仅用一个隐含层就可以逼近任意连续的非线性函数。为了使得问题表示与求解的简单，假设本文采用单输入单输出单隐含层的三层神经网络来设计控制器，定义神经网络的输出为控制器u(t)=(u1(t)，u2(t)，…，un(t))T∈Rn，第 i个神经网络的输入为:

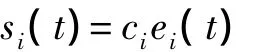
其中，ci为大于0的常数.第i个神经网络的输出ui(t)为:

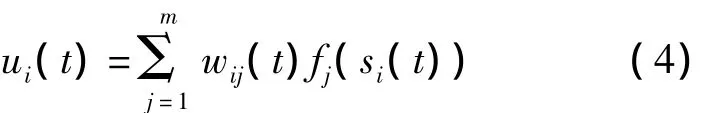
其中，i=1，2，…，n，神经网络的隐含层神经元采用s型的激励函数，其表达式为

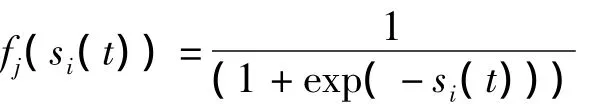
误差能量函数采用:

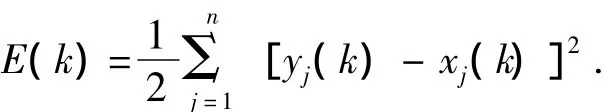
其中yj(k)为响应系统第j个状态分量的第k次输出，xj(k)为驱动系统第j个状态分量的第k次输出，E(k)为误差能量在第k次的取值。

传统的BP算法，也就是误差反向传播(负梯度方向)，它的表达式为

神经网络的学习算法采用动量BP算法，它的实质就是通过改变学习率η来提高网络性能，加入动量项表达式变为

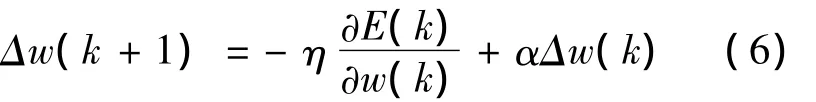
其中，动量项 αΔw(k)=α［w(k)－w(k－1)］。α为动量因子，0＜α＜1。动量项的作用在于记忆上一时刻的连接权的变化方向(即变化量的值)，这样就可以通过较大的学习速率系数η来提高学习速度。附加动量项利用其“惯性效应”来抑制网络训练中可能出现的振荡，起到了缓冲平滑的作用。

此外，附加动量项还有利于脱离平坦区。如果网络的训练已进入到了误差曲面的平坦区域，那么误差将变化很小，于是Δw(k+1)近似等于Δw(k)，而平均的 Δw(k)将变为

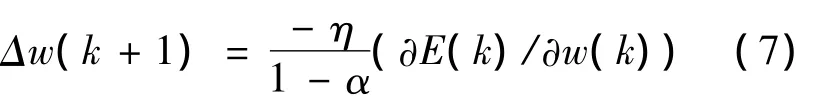
利用公式(7)可以加快误差函数沿着函数值减少最快的方向进行，从而达到混沌同步。

2 仿真实验

2.1 混沌系统描述

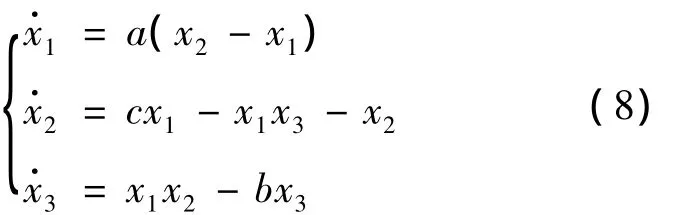
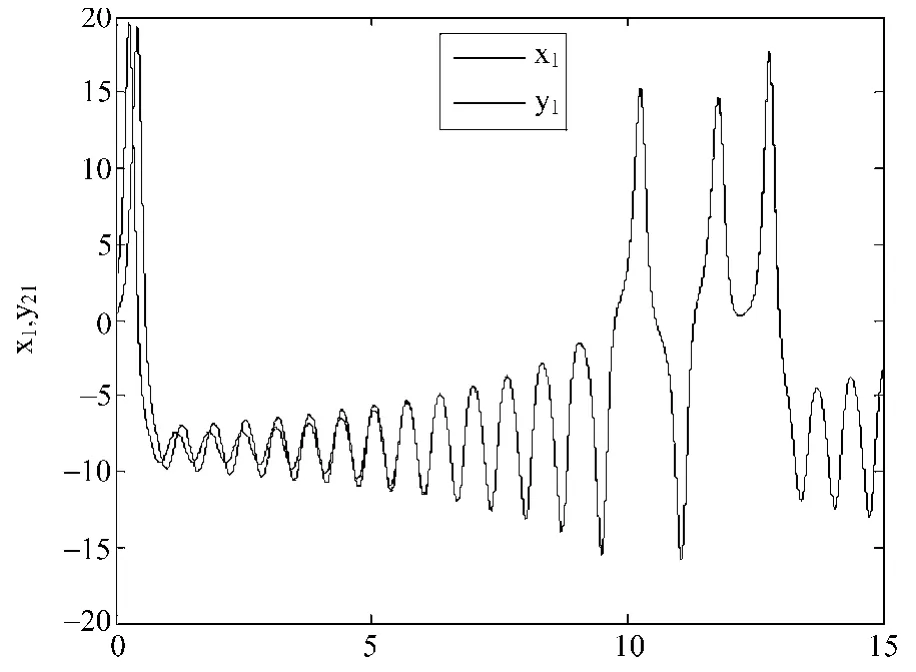
图1 主从Lorenz系统的状态变量x1(t)与y1(t)

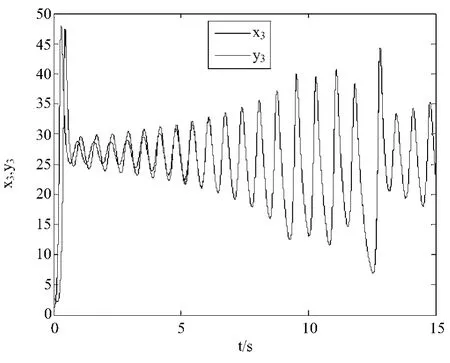
图3 主从Lorenz系统的状态变量x3(t)与y3(t)

Lorenz 系统［9，10］的数学模型为当a=10，b=8/3，c=28时，系统处于混沌状态。

2.2 Lorenz系统的同步

仿真实验中采用步长为h=0.001的欧拉公式法，主 Lorenz系统的初值选取［0.2，0.91，3］;从Lorenz系统的初值选取［3，2，1］。神经网络中的参数 c1=c2=c3=15，η =0.95，α =0.1，神经网络的隐含层个数为m=7。仿真结果如图1、2所示。图1、图2、图3分别为同步系统状态变量随时间演变曲线图，图4为神经网络的输入u1，u2，u3随时间演变曲线图。从以上仿真结果可以看出:两个系统的状态变量在利用本方法设计的控制器的作用下在较短的时间迭代后达到同步且同步的效果较好。图5给出了Lorenz系统同步时主从系统间状态跟踪误差 e1，e2，e3。

图2 主从Lorenz系统的状态变量x2(t)与y2(t)

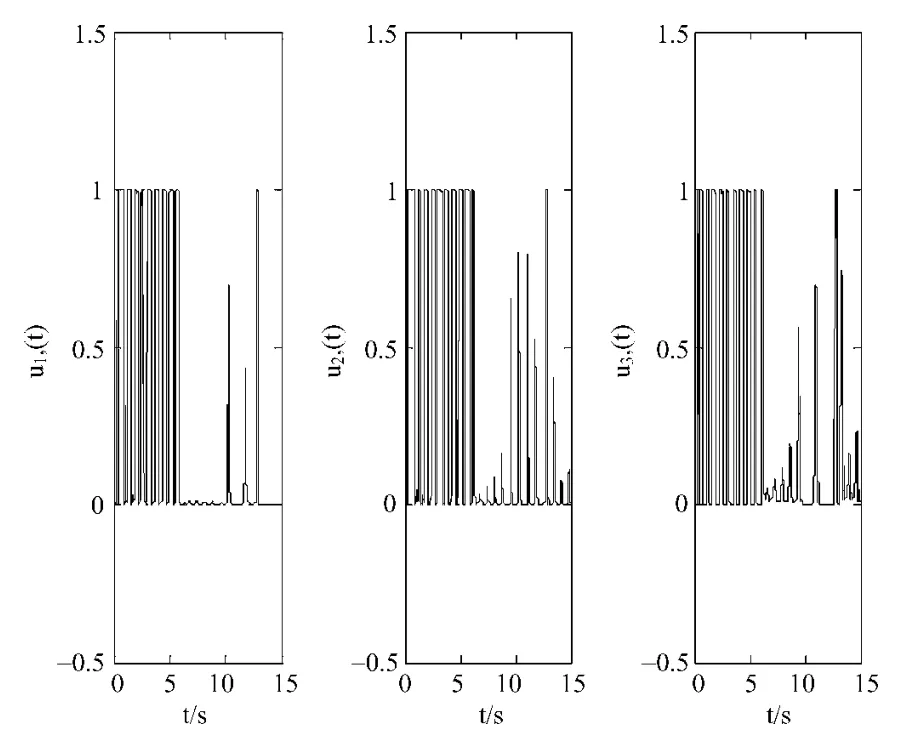
图4 Lorenz系统同步时神经网络输出随时间的演变曲线图

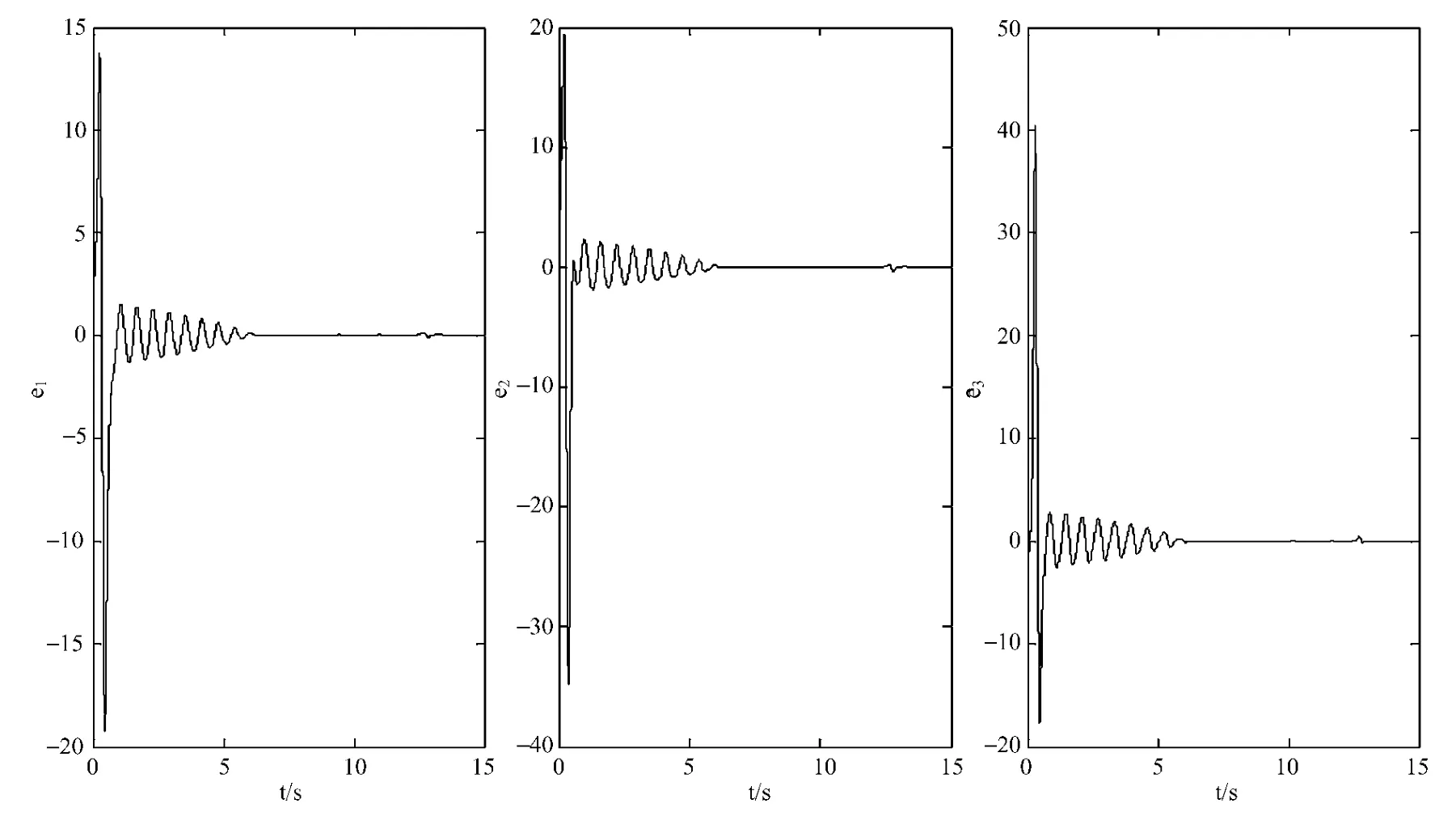
图5 Lorenz系统同步误差

2.3 保密通信仿真

为了实现基于动量BP神经网络的混沌保密通信，可按照下列步骤进行:

步骤1:先使用驱动系统产生混沌信号;

步骤2:利用动量BP神经网络控制实现响应系统与驱动系统同步;

步骤3:驱动系统与响应系统达到同步时，将模拟信号加在驱动系统产生的混沌信号中;

步骤4:通过同步的响应系统将模拟信号解密出来。

Lorenz系统的参数与上面同步实验中所选的参数相同，保密通信仿真所选的模拟信号为y=sin(x)，x∈［0，10π］，使用 MATLAB 对系统进行仿真，仿真后的结果如下图所示:图6(a)为要经过混沌系统加密的发送信号，用y表示;图6(b)为经过混沌系统加密后的信号，其中加密信号是在同步后的某个时间加入，用y1表示;图6(c)为经过控制器解密后的保密信号，用y2表示。从图中可以看出，经过混沌系统加密后保密性能非常好，经解密后保密信号能完全从加密信号中解密出来，仿真的效果很好，验证了该系统的有效性。由于加密信号只是占到了驱动系统与响应系统运行时间的一部分，故加密信号x的步长h1是与仿真步长h取值是不同的，在本文中h1=π/10，h1取值远远大于h取值，即保密信号的采样点个数远远小于混沌同步系统的采样点个数。

3 结论

本文是基于动量BP神经网络实现了混沌系统同步及保密通讯，充分利用了神经网络具有以任意精度逼近任意非线性连续函数的能力，具有较强的处理不确定性和外界干扰的能力，通过设计一组控制器，实现了混沌系统的同步。然后利用Lorenz混沌系统对本文设计的控制方法进行了验证，同步实验结果表明该方法具有良好的同步效果。最后将本文所提混沌同步方法应用于保密通信中，借助于MATLAB仿真，实现了保密通信，从仿真结果来看，验证了基于动量BP算法改进下的神经网络控制器在保密通信中的有效性与可行性。

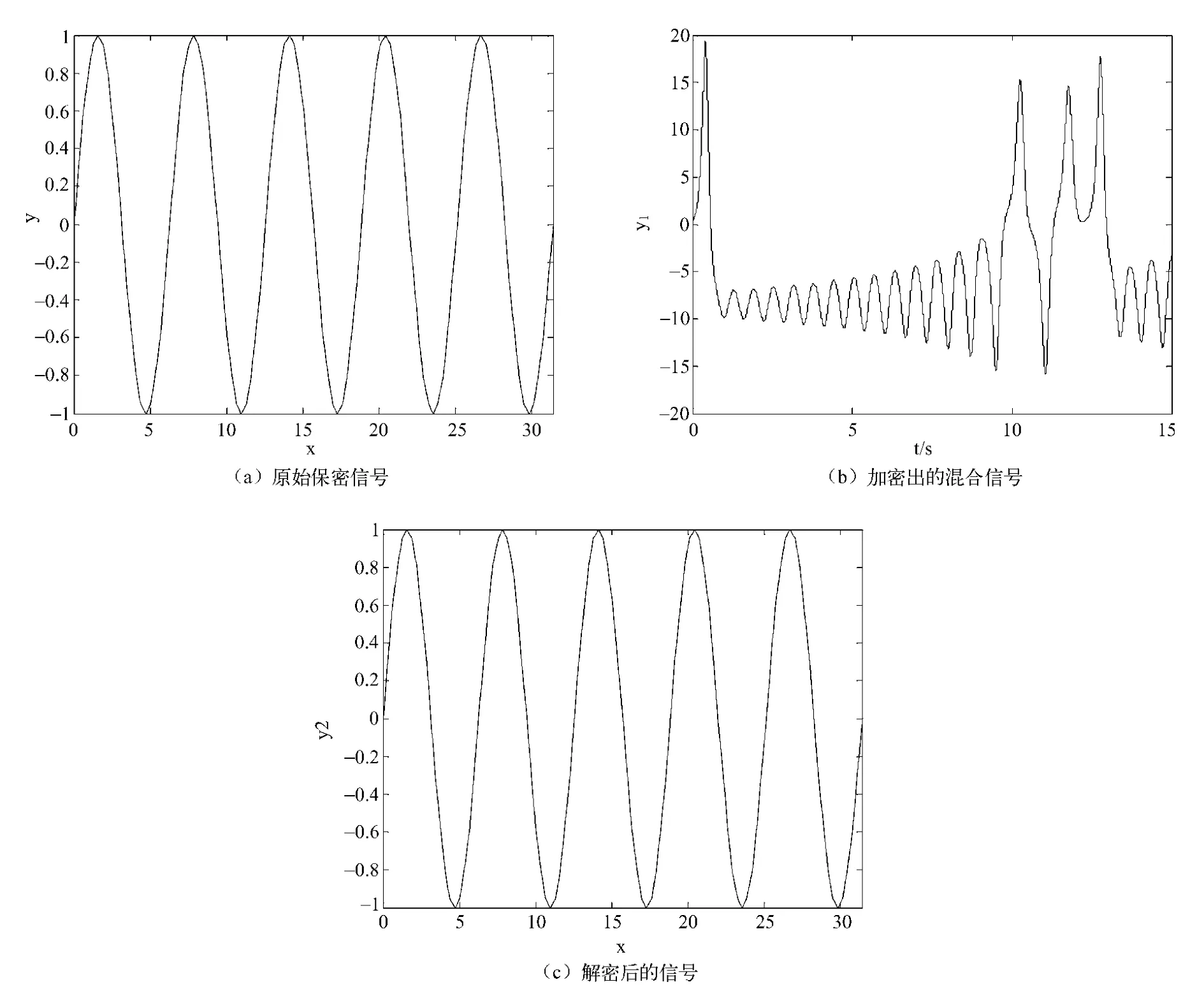
图6 Lorenz系统加密信号

［1］ 官国荣，吴成茂，贾倩.一种改进的高性能Lorenz系统构造及其应用［J］. 物理学报，2015，64(2):020501.

［2］ 江平，张定会.彩色数字图像的超混沌Lorenz系统加密［J］. 计算机测量与控制，2013，21(3):782 －784.

［3］ 王兴元.混沌系统的同步及在保密通信中的应用［M］.北京:科学出版社，2011.

［4］ 崔智勇，陈正诚.时滞扰动Lorenz系统及其同步电路实现［J］.控制理论与应用，2013，30(2):266－272.

［5］ 于灵慧，房建成.混沌神经网络逆控制的同步及其在保密通信系统中的应用［J］.物理学报，2005，54(9):4012－4018.

［6］ 刘乐柱，张季谦，许贵霞，等.一种基于混沌系统部分序列参数辨识的混沌保密通信方法［J］.物理学报，2014，63(1):010501.

［7］ 王开，裴文江，周建涛，等.一类时空混沌加解密系统的安全分析［J］. 物理学报，2011，60(7):070503.

［8］ 李贤丽，赵逢达，李贤善，等.混沌控制的现状及发展前景［J］.大庆石油学院学报，2004，28(3):102－105.

［9］ 王兴元，王明军.超混沌Lorenz系统［J］.物理学报，2007，56(9):5136－5141.

［10］ 朱夜明，乔宗敏.Lorenz超混沌系统的全局同步控制［J］.合肥工业大学学报，2007，30(8):1007－1009.