减少设备动作次数的无功优化新方法

孙守鑫，张 超，孟庆江，王 林，刘小春

（1、国网山东潍坊供电公司，山东 潍坊 261000；2、国网江西省电力公司经济技术研究院，江西 南昌 330043）

0 引言

电力系统无功优化是指从电力系统经济优化运行的角度，调整系统中各种无功控制设备，在满足节点正常功率平衡及各种安全指标的约束下，实现目标函数最小化。

传统的无功优化很少考虑到实际中的一些问题，如变压器的分接头的变动和并联无功补偿器等设备的投切次数。通过调研发现，实际运行中很少变动变压器的分接头，而主要靠投切无功补偿装置来调节无功。

从经济性角度分析，变压器分接头的调节以及其他无功设备的每次的调节和投切都将带来一定的经济损耗。从安全性角度分析，频繁的调节变压器分接头，容易产生滑档，引起电网运行的事故。

考虑到实际当中的问题，本文建立的新方法分两步求解无功优化，在传统的无功优化基础上考虑了变压器分接头的调节以及其他无功补偿设备的投切次数的约束。以负荷曲线的分段为基础，采用粒子群算法，并以IEEE30节点系统为例，证明了方法的有效性和可靠性，有实际应用价值。

1 传统电力系统无功优化

1.1 目标函数

目标函数（系统网损最小）：

1.2 约束方程

1）功率约束方程：

2）不等式约束：

2 无功优化新方法

通过现场调研，实际中往往很少调节变压器分接头，而是通过投切无功补偿装置来调节无功。考虑到实际应用情况本文提出了分两步的无功优化新方法。

2.1 具体步骤

首先，根据负荷曲线将一天的时间划分成段。划分的原则是段与段间的极差和标准差有较大变化，而段内的极差和标准差则变化较小。IEEE-30节点系统的日负荷曲线：

图1 日负荷曲线

表1为分段的结果：

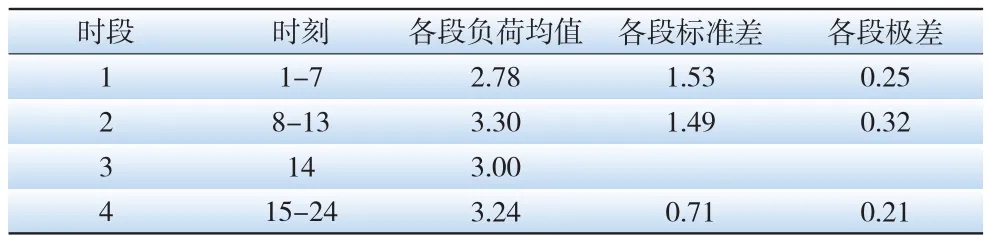
表1 分段结果

第一步应用传统的无功优化方法，在上面所分的时间段内由均值计算出无功优化最优解，求得各个时间段的系统变压器分接头的位置，分别记为。

第二步是在原有的控制变量和状态变量约束外，还要加上除变压器外的无功补偿设备投切次数的限制，即

2.2 粒子群算法

由m个粒子组成一个粒子群体，群体中每个粒子都以一定的速度移动，运动方向由两点决定：一是粒子自身移动的最好位置Pbest，二是粒子群的最好位置Gbest。其速度和位置更新公式为：

式中，i=1，…，m；d=1，2，…，n其中m为粒子群中粒子的个数；n是解向量的维数。C1和C2为大于零的学习因子，分别表示两个优化解得权重；w是惯性权重系数。

2.3 流程图

无功优化新方法流程见图2。

图2 无功优化新方法流程图

3 算例验证

为验证新方法的优越性和实际性，对IEEE-30节点实际系统进行仿真计算。采用算例系统的参数均为标幺值，电压相角单位是弧度，基准功率为100MVA。用MATLAB7.1编程实现优化计算程序。

IEEE-30节点系统包括6台发电机（节电1、2、5、8、11、13，其中1节点为平衡节点，2、5、8、11、13为PV节点）、21条负荷母线及41条支路，有4台可调变压器分布在支路（6-9、6-10、4-12、27-28）；有2个并联无功补偿装置补偿点（节点10、24）。最大迭代次数100，计算结果如表2：

表2 分时段无功优化后网损值

从表2可以看到，分段计算的无功网损要比应用原始方式计算的无功网损有明显的减少。虽然无功补偿装置的动作次数减少了，但优化的结果却得到了改善。

由表3可以看出，新方法比传统无功优化方法在变压器分接头动作方面有明显的改善，平均少动作了6.5次。

表3 变压器动作次数比较

由表4可以看到，新方法中，并联无功补偿器的平均动作次数是12.5次，比传统无功优化方法中并联无功补偿器的平均动作16次少3.5次。由于将时间分段，在每段时间内变压器为定值不动作，所以，每个变压器的动作次数最多不超过3次，使动作次数有明显减少。

表4 无功补偿器的投切次数

从图3可以看出在电压方面传统无功优化方法各节点电压的波动范围较大，新的无功优化方法节点的电压都稳定在1.0附近，使得电压质量明显的改善。有利于电压的稳定及电能质量的提高并降低网损。

图 3新方法和传统方法无功优化后电压变化

4 结论

基于对实际中主要应用调节并联无功补偿装置来调节无功，本文提出了考虑无功设备的投切次数限制的两步无功优化新方法，减少了变压器分接头的调节次数。由算例可以看出，本方法有效的减少了设备的动作次数，与传统无功优化方法对比，得到了较好的结果。

[1]刘明波，朱春明，钱康龄，等.计及控制设备动作次数约束的动态无功优化算法.中国电机工程学报，2004，24（3）:34-40.

[2]别朝红，周婷，王锡凡，电力系统多时段无功优化研究[J]，西安交通大学学报，2008，42（6）.

[3]李林川，李俊元，武文杰.考虑变压器分接头动作次数限制的综合无功优化[J].中国电力，2005，30（2）.

[4]陈建华，李先允，邓东华，等.粒子群优化算法在电力系统中的应用综述[J].继电器，2007，35（23）