一种钢轨动态轮廓数据校准方法研究*

康高强,李春茂,秦莉娟,马 俊

(西南交通大学电气工程学院,四川 成都 610031)



一种钢轨动态轮廓数据校准方法研究*

康高强,李春茂*,秦莉娟,马 俊

(西南交通大学电气工程学院,四川 成都 610031)

为减轻轨检车振动对车载视觉测量系统动态测量钢轨轮廓的不利影响,提出一种基于轮廓曲线特征点和最近点迭代算法ICP(Iterative Closest Point)的数据校准方法。通过识别动态轮廓曲线的特征点,完成数据初步校准,然后利用ICP算法确定初步校准数据与标准数据之间的变换矩阵,实现动态数据最终校准。最后通过实验模拟了振动对测量的影响。实验结果表明:在垂磨和侧磨测量点处,校准后数据与标准数据偏差值的标准差分别为0.088 mm、0.085 mm,取置信水平为0.99时,校正精度分别为±0.227 mm、±0.219 mm,该方法有较好的精度,可应用于工程测量。

视觉测量;数据校准;车辆振动;钢轨轮廓;曲线特征点;迭代最近点匹配

在铁道车辆运行过程中,由于车轮压力、轮轨接触摩擦、导向以及冲击等作用,钢轨将会出现磨耗、擦伤、波磨、剥离等缺陷。这些缺陷的形成和发展导致铁道车辆运行品质下降,缩短车辆和轨道的使用寿命,严重的会直接导致列车脱轨。因此,需要定期对钢轨的轮廓进行检测,获取钢轨的缺陷信息,为线路养护维修提供科学依据。

目前国内外高速轨检车中,激光无接触检测技术得到广泛应用,已成为轨检技术发展的主流[1-2]。在轨检车行进过程中,轨道不平顺、车辆结构等方面的原因,会引起车辆在空间内的六自由度随机振动[3]。激光摄像组件通过检测梁与列车底部相连,随车辆一起振动,因此轮廓检测数据也会受到影响。文献[4]通过实验模拟激光摄像组件相对于钢轨的位置变化,证实了振动对轮廓检测有明显的影响,并未提出解决振动影响问题的方法;文献[5]使用角点检测算法提取钢轨轮廓曲线的特征点,通过特征点来校准轮廓数据,但角点检测易受图像噪声的影响;文献[6]使用最近点迭代算法ICP(Iterative Closest Point),将实测轮廓的轨腰部分与标准轮廓的相应部分对准,仅实现了对实测数据的平移和旋转校准;文献[7]依据左右两股轨道的轨距点的坐标变化,只对垂直于钢轨的平面内的振动进行了补偿。上述文献对钢轨轮廓曲线进行了动态检测,均未完全解决振动对检测数据的影响问题。

本文在分析视觉测量原理的基础上,根据钢轨在一定长度范围内可以认为是柱体的特点,证明了在振动影响下的实测轮廓曲线与标准轮廓曲线之间存在仿射变换。在此基础上,针对我国应用最为广泛的60 kg/m钢轨,提出了基于轮廓曲线特征点和ICP配准算法的轮廓曲线校准方法,该方法不仅实现了对数据的平移和旋转校准,还实现了对数据的仿射形变校准。最后,完成了该方法的实验验证,在多种振动情况下均取得了良好的测量效果。对校准方法的特征点识别部分做相应修改,该方法也可应用于其他型号的钢轨。

1 测量系统简介

激光摄像组件主要由线激光器、高速面阵式CCD摄像机以及机械安装装置组成,轮廓测量原理如图1所示。激光摄像组件安装在列车底部的检测梁上,线激光器投射出的光平面与钢轨纵向垂直,在钢轨表面形成高亮的测量光条。摄像机与线激光器安装在钢轨的同一侧且与光平面成一定夹角,摄像机实时拍摄光条图像,基于图像处理技术和视觉测量原理,计算出钢轨轮廓数据。

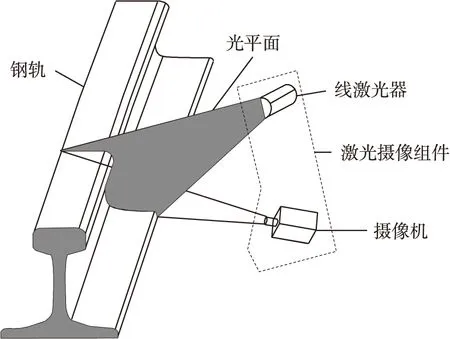
图1 系统测量原理示意图

在动态测量过程中,激光摄像组件随检测车一起沿钢轨运动,实现对钢轨轮廓的实时动态测量。由于车辆在行进过程中的随机振动,激光摄像组件相对于钢轨的位置将会变化,这将对测量数据造成不可忽略的影响。如何消除振动对测量数据的影响,是钢轨轮廓动态测量过程中所要解决的关键问题。

2 视觉测量模型

为建立由摄像机和线激光器组成的视觉测量系统的数学模型,建立如图2所示的坐标系,Ocxcyczc为摄像机坐标系,Ouxuyu为图像坐标系,建立世界坐标系Owxwywzw使平面Owxwyw与光平面重合,Owxwyw即为二维测量坐标系,则光平面在世界坐标系Owxwywzw下的方程为zw=0。

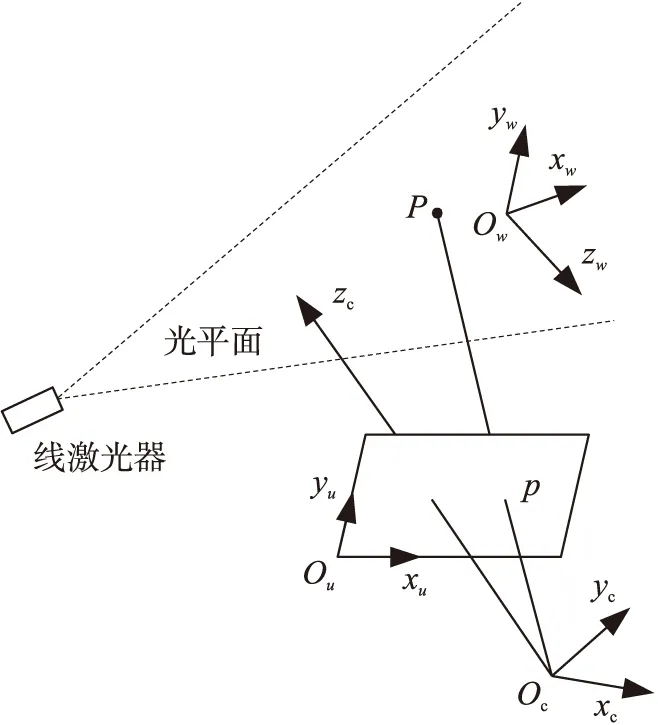
图2 视觉测量系统标定示意图

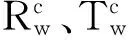
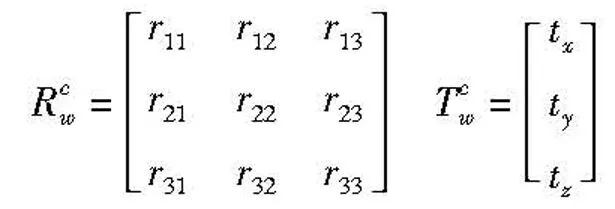
由摄像机成像模型有

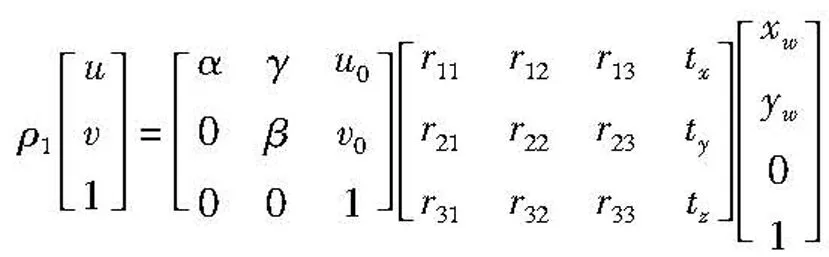
(1)

式中,ρ1≠0,(α,β,γ,u0,v0)为摄像机的内部参数。

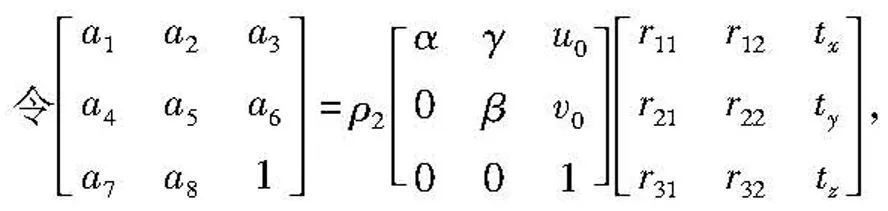
ρ=ρ1ρ2,由式(1)得

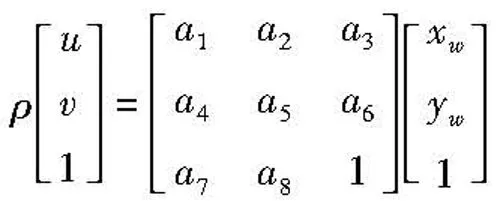
(2)

由式(2)即可确定光平面(测量平面)中任一点的像点在图像平面内坐标。

在使用该测量模型进行实际测量时,要先对视觉测量系统的参数进行标定。具体的标定方法,参阅文献[8-11]。

3 钢轨轮廓数据的校准原理及方法

3.1 钢轨轮廓数据的校准原理

在动态测量过程中,由于轨道不平顺、车辆结构等方面的原因,车辆将会发生随机振动,激光摄像组件相对于钢轨的姿态将会变化,因此轮廓测量数据也会受到影响。当光平面保持与钢轨纵向垂直时,动态轮廓曲线与标准轮廓曲线形状相同,只是同一平面内平移和旋转;当两者不再垂直时,因为光平面“切割”钢轨的角度发生了变化,动态轮廓曲线会发生变形。钢轨轮廓数据校准,即通过钢轨未磨损部分的动态测量数据与标准数据对比,计算出两者之间的变换关系,对动态测量数据进行校准,消除振动对测量数据的影响。

在动态测量过程中,线激光器与摄像机的相对位置不变,式(2)依然成立,但由于激光摄像组件相对于钢轨的姿态变化,动态测量坐标系相对于标准测量坐标系将会发生如图3所示的旋转和平移。

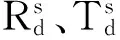
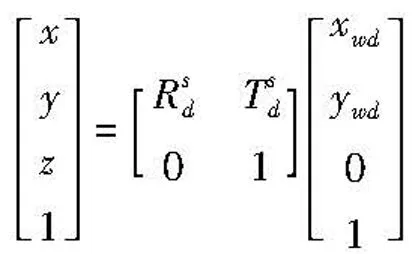
(3)

假设钢轨没有磨损,在一定长度范围内是一理想柱体,则动态轮廓与标准轮廓之间存在仿射变换的关系。设仿射变换为[A1T1],则有

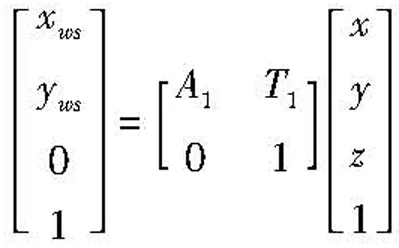
(4)

将式(3)代入式(4),可得动态轮廓的坐标(xwd,ywd)与标准轮廓的坐标(xws,yws)之间满足

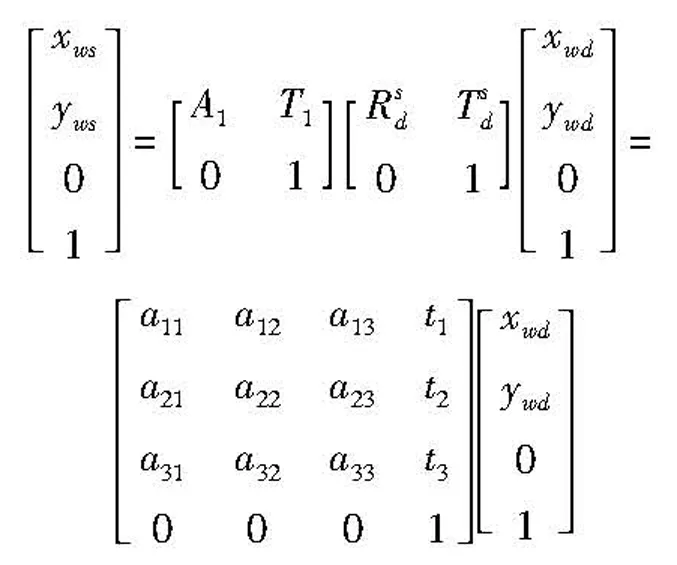
(5)

化简得

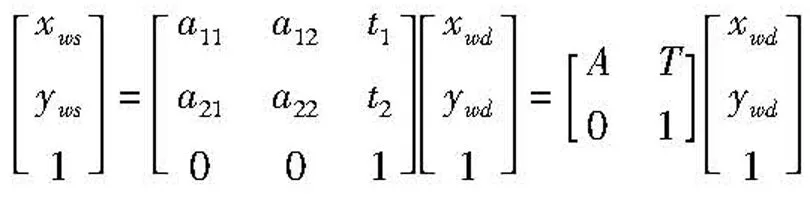
(6)

由式(6)知,动态轮廓与标准轮廓之间存在仿射变换。在以上分析中,以钢轨没有磨损为前提,实际应用中钢轨是有磨损的,但轨头以下部分不与车轮接触没有磨损,因此这部分轮廓与标准轮廓的相应部分之间仍满足式(6)。通过钢轨未磨损部分的动态轮廓数据求出仿射变换[A T],即可完成对测量数据的校准。

3.2 钢轨轮廓数据校准方法

设标准数据为S={si,i=1,2,…,m},测量数据为D={di,i=1,2,…,n},对点集中D一点di,点集中S与di欧氏距离最小的点称为它的最近点。标准ICP算法[12],通过搜索数据点集中每点di在标准数据点集S中的最近点,然后通过迭代优化使最近点对之间距离平方和最小,从而确定两点集之间的旋转矩阵Rb和平移向量Tb,即以

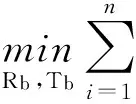
(7)

为目标函数寻求最优的Rb和Tb。

钢轨未磨损部分的动态轮廓数据与标准轮廓的相应部分之间存在仿射变换[A T],将标准ICP算法中的目标函数替换为

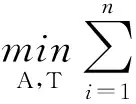
(8)

然后进行迭代,即可求出[A T]。但如果直接进行迭代优化,由于A不是对称阵,要优化的参数较多(6个),迭代过程收敛较慢且求解的精度有待进一步提高。

针对以上问题,本文首先对参数进行解耦,然后再求取最优解。60kg/m标准钢轨截面如图4所示,轮廓曲线由圆和直线连接构成,其中点Ps是两直线的交点,以点Ps为原点建立标准测量坐标系Owsxwsyws。

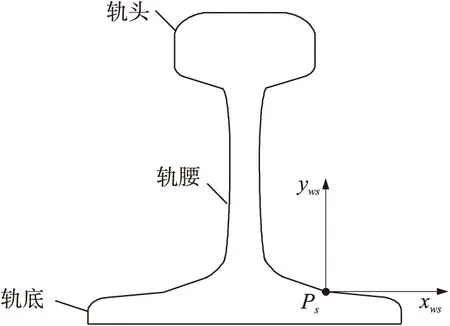
图4 60 kg/m标准钢轨截面图

仿射变换保持数据点的共线性,直线变换后仍是直线,在仿射变换下轮廓测量数据中两直线的交点Pd映射为标准轮廓数据中的Ps。因此可以从测量轮廓中识别出特征点Pd,对测量数据进行整体平移,使点Pd与点Ps重合,完成数据的初步校准。然后以

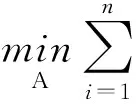
(9)

为目标函数,对A进行优化,完成数据的最终校准。校准算法的流程见图5。

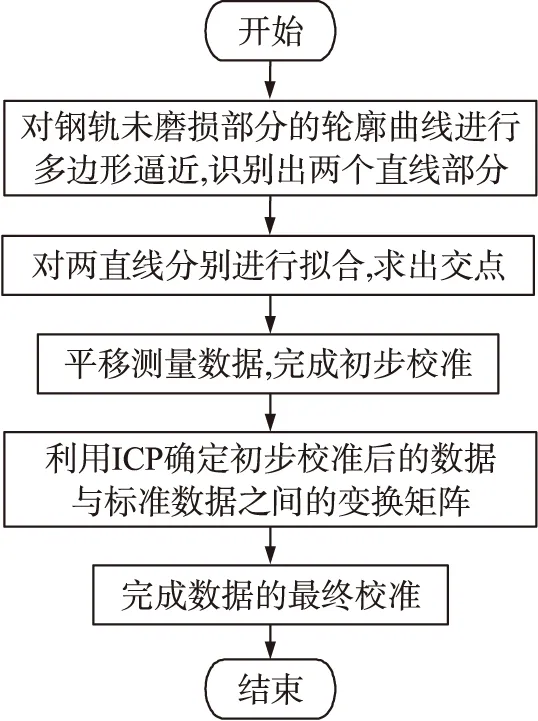
图5 校准算法的流程图

为了使参数达到最优,需要解决的关键问题有两个:特征点的精确提取和最近点的快速搜索。

3.2.1 特征点提取

为了求取特征点Pd的坐标,首先要将测量轮廓中的两条线段分离出来,然后拟合直线到这两条线段上,他们的交点即为所求。

将轮廓曲线分割成直线,可以通过轮廓曲线的多边形逼近实现。对于测量轮廓D={di,i=1,2,…,n},用一多边形对其进行逼近,就是寻找D的一个子集,此子集保留了原轮廓的重要几何信息。轮廓曲线与多边形每条边对应的部分,均可用直线很好地近似。Ramer逼近算法是一种递归算法[13],首先用线段连接轮廓曲线的两端点,然后计算所有的轮廓点到线段的距离并找到与线段距离最大的轮廓点,如果此距离比预设的阈值要大,那么在具有最大距离的轮廓点处再将当前的轮廓分为两段,然后重复以上过程,直到所有的线段都满足最大距离约束。通过设置合适的阈值,将轨腰轮廓曲线进行适度分割,其中最长的两段即为钢轨轮廓曲线中的直线部分。

摄像机拍摄光条图像的过程中,由于钢轨表面的氧化、污染等因素的影响,光条图像将会发生不同程度的畸变,另外Ramer算法产生的多边形顶点与真实的曲线拐角处也会有稍许偏差,因此必须用鲁棒性好的算法对直线进行拟合才能获取高精度的特征点。本文采用带权重系数的直线拟合方法,该方法以

(10)

为目标函数,对直线参数α,β,γ进行优化,式中ωi为Tukey权重系数、λ为拉格朗日乘数。

3.2.2 最近点搜索

在ICP算法执行过程中,寻找最近点需要进行大量的搜索,这是ICP算法的速度瓶颈。Kd树作为一种空间索引方法,它将二分查找树的思想推广到多维数据的情况,利用点集中元素之间的空间位置关系将点集有效地组织起来,提高了搜索效率[14]。二维数据点拥有x和y两个坐标值,首先将数据点集沿x坐标方向做一次划分,然后沿y坐标方向做一次,接着x坐标方向再次划分,如此下去即可生成一个Kd树。

列车行进过程中激光摄像组件相对于钢轨的姿态变化有一定限度,光条在图像中的位置变化有限,因此最近点搜索不需要对全体数据进行搜索,在一定坐标范围内搜索即可。将标准轮廓数据S={si,i=1,2,…,m}为3个子集S1∪S2∪S3=S,然后建立3个分别与S1、S2、S3对应的Kd树。在最近点搜索过程中,首先根据数据点的坐标确定它的最近点应在的子集,然后在相应的Kd树中完成搜索,这样可以提高搜索速度。其中S1与S2、S2与S3分别有20个数据点的交集,这样可以避免分割点附近出现最近点的错误匹配。

4 实验

在实验中,首先在光平面与被测钢轨纵向垂直时对钢轨轮廓进行测量,并以测得的数据作为标准数据,然后通过移动和旋转钢轨来模拟振动对检测的影响,同时完成动态轮廓数据的测量,最后通过比较校准后的动态轮廓与标准轮廓在轨头部分的偏差,验证校准原理的正确性以及校准方法的有效性。

采用MicroviewCCD摄像机,分辨率为1 280×1 024像素,德国Z_Laser线激光器,线宽小于0.2mm,软件平台为MATLAB,测量对象为一段长0.5m表面有锈蚀与现场钢轨反光特性相似的60型钢轨。

当光平面与被测钢轨纵向垂直时,相机拍摄的光条图像如图6(a)所示,提取光条的亚像素中心,利用已标定的视觉测量模型参数,得到钢轨的标准轮廓数据如图6(b)所示。

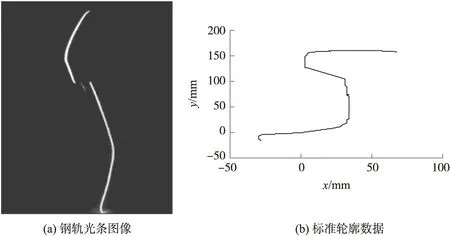
图6 钢轨轮廓数据采集

通过改变钢轨的姿态来模拟振动对测量的影响,在±50 mm范围内平移钢轨模拟车辆的浮沉和横摆运动,在±5°范围内旋转钢轨模拟车辆的侧滚、摇头和点头运动,对钢轨轮廓数据进行动态测量的数据如图7(a)所示,通过识别出轮廓的特征点对轮廓数据进行初步校准的结果如图7(b)所示,利用ICP算法对初步校准后的数据进行再次校准的结果如图7(c)所示,局部放大后如图7(d)所示。校准后的动态轮廓与标准轮廓基本重合,基本消除了振动对测量数据的影响,提高了测量精度。

在钢轨姿态不同的情况下,对钢轨轮廓进行20次测量,表1给出了数据校准后与标准数据在垂磨测量点处的偏差值dv和侧磨测量点处偏差值dh的计算结果[15]。

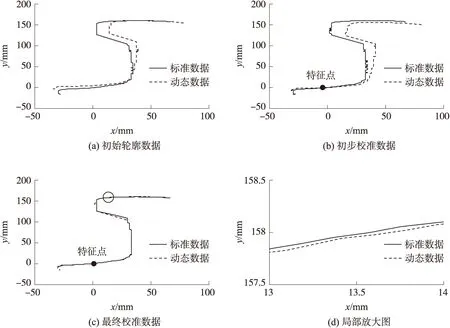
图7 轮廓数据校准过程

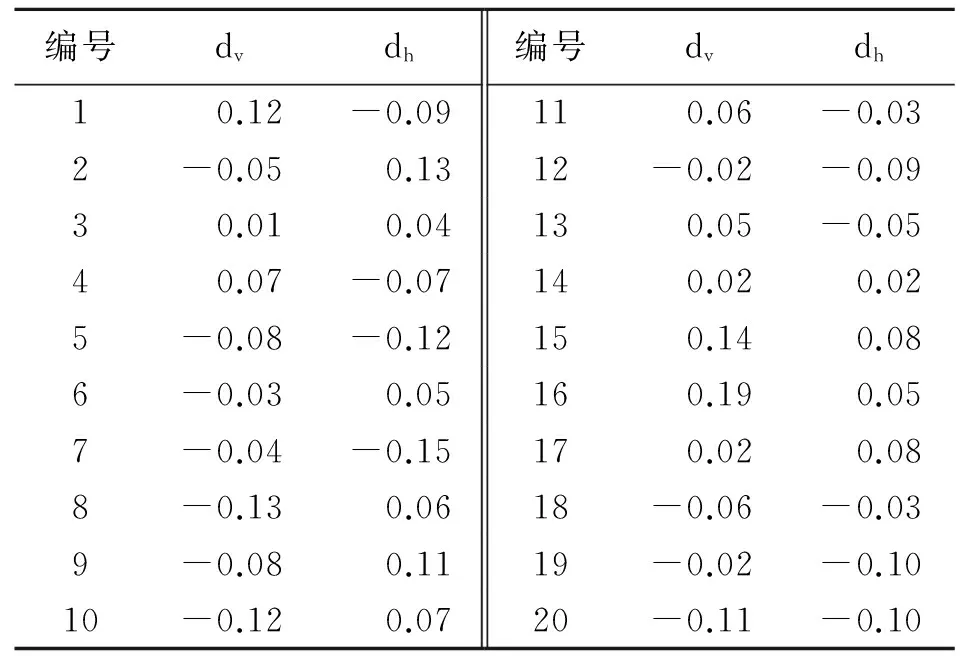
表1 校准后数据与标准数据的差值 单位:mm

在测量过程中钢轨的姿态在一定范围内进行了随机变化,模拟了各种振动情况,表1中所测得20组数据能够有效评价校准方法的有效性。测量过程受很多相互独立因素的影响,测量误差理应服从正态分布,经检验确实如此。由表1可见,校正后的轮廓数据与标准数据的偏差dv、dh的标准差分别为0.088mm、0.085mm,取置信水平为0.99,校正精度分别为±0.227mm、±0.219mm。综上可知,校准算法具有较高的精度,可应用于工程测量。

5 结论

证明了在振动影响下的实测轮廓曲线与标准轮廓曲线之间存在仿射变换关系,针对我国应用最为广泛的60kg/m钢轨,提出了一种基于轮廓曲线特征点和最近点迭代算法确定仿射变换参数、校准实测数据的方法。该方法能够基本消除车辆在空间中的六自由度振动对测量数据的影响,提高了测量精度。随着我国高速铁路事业的发展,对钢轨轮廓检测的速度、精度要求越来越高,本文为提高检测精度和速度提供新的思路和技术参考

[1] 陈东生,徐其瑞.GJ-5型轨道检查车[M].北京:中国铁道出版社,2013.

[2]魏世斌,李颖,赵延峰,等.GJ-6型轨道检测系统的设计与研制[J].铁道建筑,2012,2:97-100.

[3]严隽耄,傅茂海.车辆工程[M].北京:中国铁道出版社,2008.

[4]何红涛,何长江,李华文,等.应用微机图像处理技术实现钢轨磨耗自动测量的研究[J].铁道学报,1994,16(4):43-49.

[5]Jin Wenrui,Zhan Xingqun,Jiang Benhe.Non-Contact Rail-Wear InSpecting System Based on Image Understanding[C]//Proceedings of the 2007 IEEE,International Conference on Mechatronics and Automation.Harbin,China,2007:3854-3858.

[6]孙军华,王伟华,刘震,等.基于结构光视觉的钢轨磨耗测量方法[J].北京航空航天大学学报,2010,36(9):1026-1029.

[7]占栋,于龙,邱存勇,等.钢轨轮廓测量中的车体振动补偿问题研究[J].仪器仪表学报,2013,34(7):1625-1633.

[8]刘涛,贾刚,王宗义.一种基于运动的线结构光视觉测量系统标定方法[J].传感技术学报,2011,24(4):624-628.

[9]Zhang Zhengyou.A Flexible New Technique for Camera Calibra-tion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.

[10]周富强,张广军,江洁.线结构光视觉传感器的现场标定方法[J].机械工程学报,2004,40(6):169-173.

[11]马玉坤,王中亚,杨国威,等.基于线结构光传感器的公路平整度测量系统[J].传感技术学报,2013,26(11):1599-1603.

[12]Paul J Besl,Neil D Mekay.A Method of Registration of 3-D Shapes[J].IEEE Transactions on Patten Analysis and Machine Intelligence,1992,14(2):239-256.

[13]Ramer U.An Iterative Procedure for the Polygonal Approximation of Plane Curves[J].Computer Graphics and Image Processing,1972,1:244-256.

[14]Zhang Zhengyou.Iterative Point Matching for Registration of Freeform Curves and Surfaces[J].International Journal of Computer Vision,1994,13(2):119-152.

[15]中华人民共和国铁道部.铁路线路修理规则(铁运[2006]146号)[S].北京:中国铁道出版社,2012.

Research on A Method of Calibrating Dynamic Rail Profile Data*

KANGGaoqiang,LIChunmao*,QINLijuan,MAJun

(School of Electric Engineering,Southwest Jiaotong University,Chengdu 610031,China)

To alleviate adverse effects of track inspection car vibration on car-mounted vision measurement system while measuring rail profile dynamically,a data calibration method based on profile curve feature point and iterative closest point(ICP)algorithm is proposed.Dynamic data is calibrated preliminarily by identifying the profile curve feature point,and then the transformation matrix between the preliminarily calibrated data and the standard data is determined by ICP algorithm,finally the data calibration is completed.The impact of vibration on measurement is simulated in the experiment,and then the deviation value between the calibrated data and the standard data is measured at both vertical and horizontal wear measuring points,standard deviation respectively 0.088 mm,0.085 mm,take 0.99 confidence level,precision respectively±0.227 mm,±0.219 mm.Experimental results show that the method has good repeatability precision,can be applied to engineering measurements.

vision measurement;data calibration;vehicle vibration;rail profile;curve feature points;iterative closest point

康高强(1986-),男,河南周口人,硕士研究生,主要从事视觉测量、图像处理方面的研究,kanggqyyy@163.com;

李春茂(1963-),男,重庆人,工学博士,教授,主要研究方向为控制理论与控制工程、电工理论与新技术,chunmaoli@126.com。

项目来源:国家“863”计划项目(2011AA11A102)

2014-09-09 修改日期:2014-11-25

C:7130;7210

10.3969/j.issn.1004-1699.2015.02.013

TP391

A

1004-1699(2015)02-0221-06