两级量测更新的粒子滤波检测前跟踪算法*

陈延军,梁新华,潘 泉,梁 彦

(1.西安石油大学光电油气测井与检测教育部重点实验室,西安 710065;2.西北工业大学自动化学院控制与信息研究所,西安 710072)



两级量测更新的粒子滤波检测前跟踪算法*

陈延军1*,梁新华2,潘 泉2,梁 彦2

(1.西安石油大学光电油气测井与检测教育部重点实验室,西安 710065;2.西北工业大学自动化学院控制与信息研究所,西安 710072)

针对低信噪比下弱目标的检测与跟踪问题,提出了一种基于两级量测更新的粒子滤波器检测前跟踪算法。算法在粒子滤波状态更新之后,在其状态估计附近,引入卡尔曼滤波框架,进行第2级的量测更新,提高了粒子携带信息的利用程度。仿真结果表明,新算法获得了更好的检测和跟踪性能。

弱小目标;检测前跟踪;粒子滤波;两级量测更新

检测前跟踪TBD(Track-Before-Detect)是相对传统先检测后跟踪的一种处理方法。TBD可以综合对信号和数据进行处理,或综合处理连续多帧/多次扫描的原始量测,同时宣布目标出现与航迹的形成[1]。TBD可以更充分地利用量测信息,是处理低信噪比目标检测与跟踪的有效思路。

在众多TBD方法中,基于粒子滤波PF(Particle Filter)或序贯蒙特卡罗SMC(Sequential Monte Carlo)的递归TBD方法是研究热点之一[1],其中单目标问题是早期研究的重点。基于粒子滤波的单目标TBD——PFTBD(Particle Filter based Track Before Detect)先由Salmond等人[2]提出,其采用一种经典的多模型粒子滤波的方法实现,后Ristic[1]等人对该算法的实现及其性能进行了详细分析,并由Boers等完善了粒子检测理论[3]。而Rutten等人则在上述研究的基础上,提出一种更高效的PFTBD算法[4-5]。此后的研究包括Maskell S R的分布式PFTBD的融合算法[6],Hlinomaz的多速率多模型PFTBD算法等[7]。国内学者龚亚信在似然比检测[8]、李翠芸和吴孙勇等在粒子滤波几个变种改进PFTBD[9-13]、雷达应用[11,14]等方面做了大量研究,但大多仍在Salmond算法架构下进行,且考虑算法效率问题较少。对于红外凝视型传感器的单目标PFTBD问题,梁新华等分别从分级降维及局部搜索的角度提高采样效率[15-16]。

在多目标PFTBD研究中,Li Cuiyun等综合了两种单目标PFTBD算法架构,把多目标的TBD问题分为搜索与跟踪两个子过程,分别用Salmond和Boers的架构实现,并采用Rao-Blackwellized粒子滤波提升性能[12]。近几年基于随机有限集RFS(Random Finite Sets)的滤波器如概率假设密度滤波器PHD(Probability Hypothesis Density)和多目标多贝努利滤波器MeMBer/MB(Multi-target Multi-Bernoulli)也被应用于TBD问题中。Punithakumar等首先将SMC-PHD方法应用于多目标的检测前跟踪[17]。针对TBD的量测模型不满足PHD滤波器的假设的问题,童慧思提出一种对TBD中的量测模型进行“标准化”和噪声的“泊松化”处理后进行PHD滤波的算法[18-19],后又提出一种基于Shrinkage的增强型PHD-TBD算法,性能有较大提升[20]。林再平等修正了Punithakumar的PHD更新公式,提出一种SMC-PHD的TBD算法及其平滑算法[21-22]。此外还有基于MeMBer滤波器的SMC-TBD方法[23]。

本文以文献[5]的算法为基础,提出一种基于二级量测更新的单目标PFTBD改进算法。其核心思想是在粒子滤波状态估计之后,以其得到的检测与估计信息为基础,采用卡尔曼滤波机制进行第2次量测更新,提高了粒子采样信息的利用程度,最终改善了粒子的采样精度和多样性。仿真结果表明新算法获得了更好的检测与估计性能。

1 问题描述

1.1 目标模型

假设目标状态服从离散线性高斯匀速运动模型,即

sk=Fsk-1+Vk

(1)

其中Vk是零均值高斯过程噪声,方差为Q。目标状态向量为5维,包括x和y方向的位置、速度、目标强度,即:

(2)

状态转移矩阵

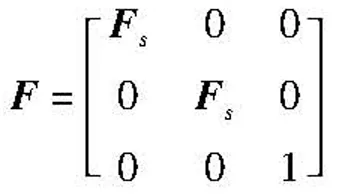
(3)

过程噪声协方差

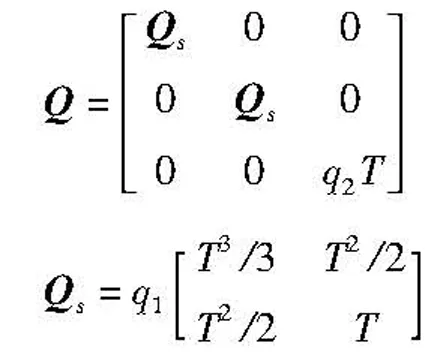
(4)

其中T为采样周期,q1为加速度噪声的功率谱密度,q2为目标回波强度噪声的功率谱密度。时刻k目标是否存在于观测区域内,以目标存在性变量Ek描述。其建模为一个二态Markov链,即Ek∈{0,1},Ek=0表示目标不存在,Ek=1表示目标存在。定义目标的出现概率和消失概率分别为:

Pb=P{Ek=1|Ek-1=0}

(5)

Pd=P}Ek=0|Ek-1=1}

(6)

则概率转移矩阵为:

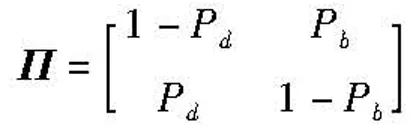
(7)

1.2 观测模型

这里的观测模型是广为采用的凝视型红外传感器观测模型[1-2,5]。传感器信号处理后原始量测为序列图像。每一帧图像为npixel×mpixel,每个像素对应一个大小为Δx×Δy的矩形区域,时刻k的量测为图像每个像素单元的强度。在像素单元(i,j),i=1,…,n,j=1,…,m处的量测强度定义为:

(8)

(9)

其中Σ为红外传感器模糊系数。

2 基于两级量测更新的PFTBD算法

在众多的TBD算法中,PFTBD是研究热点之一。PF可以较为有效处理非线性和非高斯问题,还可以将检测、跟踪和识别等问题在概率框架下集成,并且方便引入许多先验信息。在PFTBD研究方面,一些学者将PF的各种变种引入到PFTBD中来,用以提升算法性能,如辅助粒子滤波(APF)、Rao-blackwellised粒子滤波(RBPF)以及不敏粒子滤波(UPF)等。但是这些研究大多仍然基于Salmond的算法架构,并且没有过多考虑算法效率问题。

从PF的研究进展看,在同等计算复杂度要求下,许多PF改进算法的性能提升相对PF并不十分明显,有时可能还不如直接增大粒子数目效果好。最近,文献[16]提出一种新的粒子滤波算法,其综合PF和卡尔曼滤波器(KF)两种不同的机制进行状态估计,综合性能优于PF和大多数的PF变种。其吸收样本的二阶矩信息,通过KF机制,修正PF的估计。本文借鉴文献[24]的研究成果,提出一种基于两级量测更新的PFTBD(Two-Stage Measurement Update Particle Filter based Track Before Detect,TPFTBD)算法。这里仅给出在Rutten的算法架构[4-5]下的改进算法步骤:

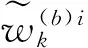
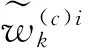
③根据上面2个非归一化权重计算混合概率。

(10)

⑦由第(4)步的合并后的粒子集和权重集计算卡尔曼滤波机制下的状态一步预测。

(11)

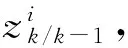
(12)

(13)

(14)

⑩计算KF机制下的状态预测误差协方差Pk/k-1、状态与量测的预测误差协方差Pxz以及量测预测协方差Sk。

(15)

(16)

(17)

Kk=Pxz(Sk)-1

(18)

(19)

Pk/k=Pk/k-1-KkSkKk

(20)

(21)

其中ei～μ(0,1),为服从0至1区间均匀分布的随机数。ζ为转移控制参数,且ζ∈[0,1],其大小影响着重采样后粒子多样性改善程度。

由以上步骤可以看出,步骤①～步骤⑥是Rutten的原PFTBD算法步骤,步骤⑦～步骤为新增的KF机制下的更新步骤。这种新增机制的引入,充分利用了基于PF机制下的估计信息,如果某个时刻目标出现并处于PF的估计位置附近,那么第2级量测更新将获得目标状态更加精确的估计,并将其反馈到重采样后的粒子采样中,可以提高下一时刻的粒子采样效率,进而获得更好的检测与估计性能。新的算法复杂度略有增加,但算法效率有很大的提升,仿真实验证实了这一点。

3 仿真实验和结果

以一个在二维平面内的单个目标场景来比较两种算法的性能。原PFTBD算法和本文改进算法(TPFTBD)采用相同的参数,设置观测噪声方差得到不同的信噪比。Nc=Nb,总粒子数目原算法为N=2 000,改进算法的粒子数分别为N=2 000与N=1 000,依次在1到9dB下各做3 000次仿真。其他参数设定如下:

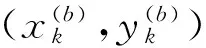
3.1 在6 dB下的情形

下面以SNR=6 dB下的情形为例进行仿真分析。多次仿真平均意义下的目标存在概率曲线如图1所示,图2给出了不同虚警概率下的检测概率,即ROC(Receiver Operating Characteristic)曲线。图3给出了位置估计的均方根误差随时间变化曲线。

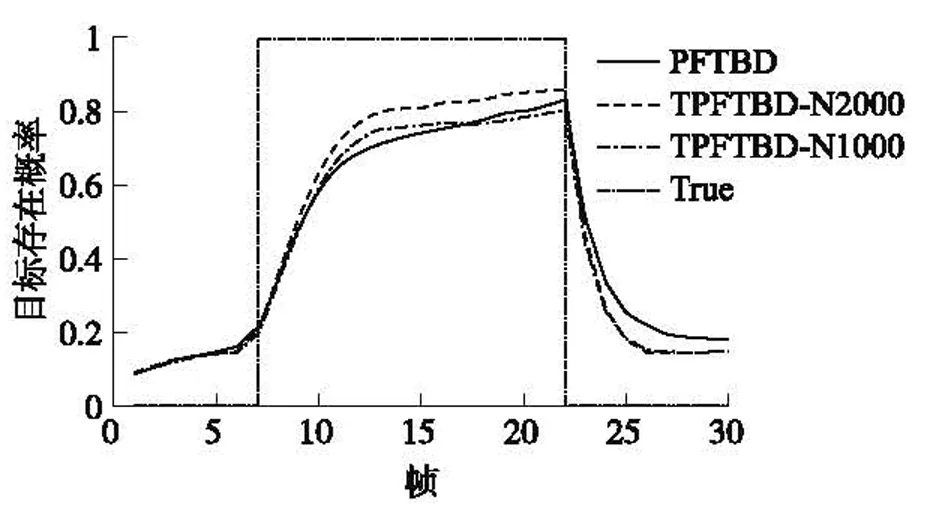
图1 目标存在概率估计

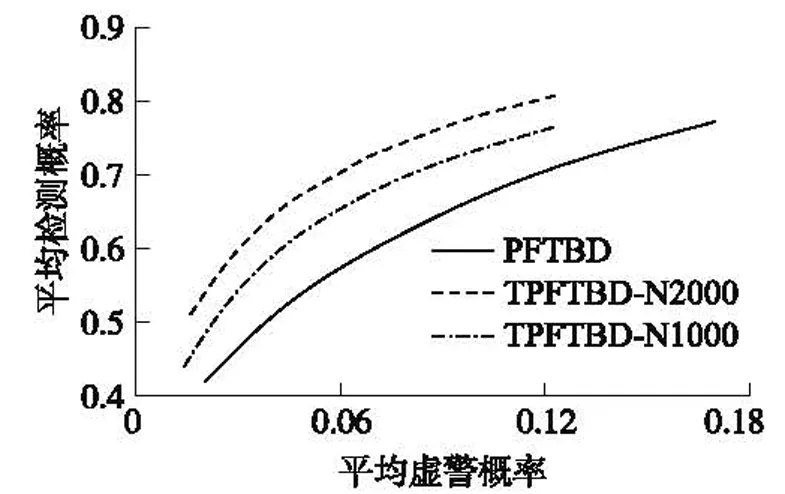
图2 检测性能ROC曲线

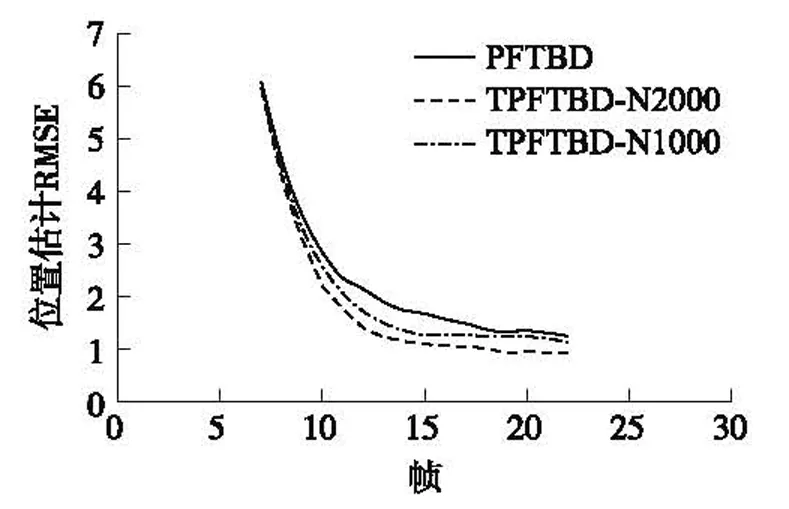
图3 位置估计误差

由图1～图3可以看出,改进算法较原算法获得了更高的检测性能和估计精度,改进算法在N=1 000时的性能仍然高于原算法在N=2 000下的性能。

3.2 不同信噪比下的性能

图4还给出了原算法和改进算法在1到9 dB下的平均检测概率对比曲线,这里固定虚警概率为0.05。从图4可以看出,在同等粒子数的情况下TPFTBD相对原算法可以获得1个dB以上的增益,而N=1 000下的TPFTBD相对原算法在N=2 000可以获得0.5个dB左右的增益。但是也会发现在很低信噪比(比如3 dB)以下通过增加粒子数或其他改进方法,检测与估计性能的提升效率也逐渐变小,这是因为在较低信噪比下,存在许多与真实目标量测相似的虚假量测。而在较高信噪比下,比如8 dB以上时,也发现第2阶段的更新获得的收益也变小,特别是N=1 000下的TPFTBD相对优势变小较多,这是因为高信噪比下较多粒子容易较早地捕获真实目标位置,粒子很快会大量聚集在目标附近,第2阶段的更新对估计精度和粒子多样性的增强改善有限。

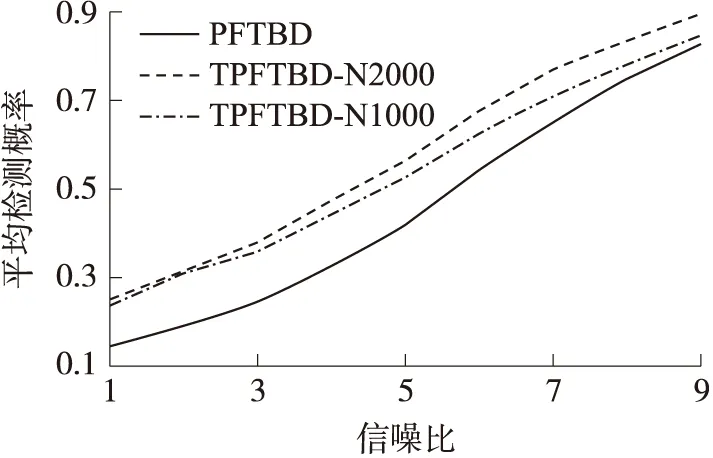
图4 不同信噪比下的检测性能

表1给出了两种算法的单次仿真平均运行时间对比。从中可以看出,在同等粒子数情况下改进算法计算量略有增加,约为10%～20%。但N=1000下的TPFTBD只需PFTBD 55%～60%左右的运算时间就可以达到或者超过PFTBD在N=2 000的性能。而增大总粒子数也可以得到上述结论。

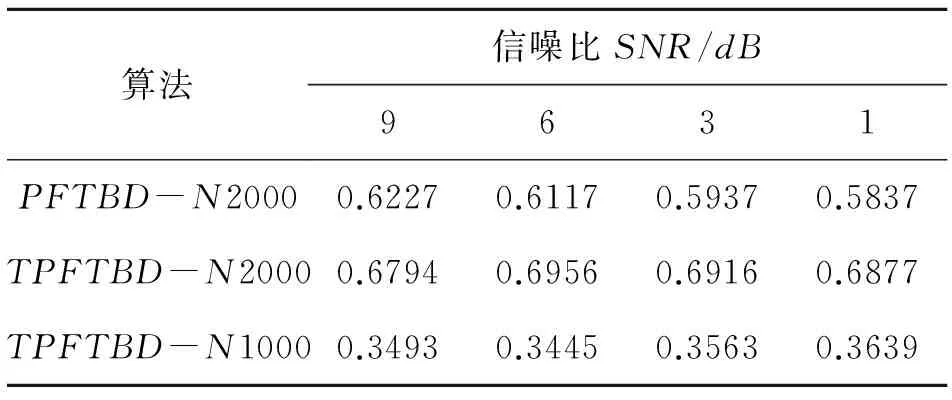
表1 单次仿真平均时间(s)

3.3 关于转移控制参数ζ的选择

在前面的仿真实验中我们选择ζ=0.6,并没有给出特别的理由。显然如果ζ选择较大,则只有小部分粒子携带第2次更新后的估计信息,特别地ζ=1则第2次更新对粒子后验分布没有任何修正,粒子的多样性未得到增强;相应地若选择ζ<0.5则大部分粒子的状态被修正,整体后验分布受到较大程度的干扰。下面我们通过仿真实验的形式进行分析这一参数对算法性能的影响,仍以SNR=6 dB下的情形为例进行分析。原PFTBD算法粒子数N=2 000,改TPFTBD算法粒子数为N=1000,转移参数选择ζ=1,0.9,0.6,0.4,在下面的仿真实验和分析中,TPFTBD-N1000-1表示TPFTBD算法在N=1000且转移参数ζ=1这种参数组合,其他参数组合以此类推。图5给出了上述两种算法共5种参数组合在不同虚警概率的检测概率,图6给出了位置估计的均方根误差曲线。

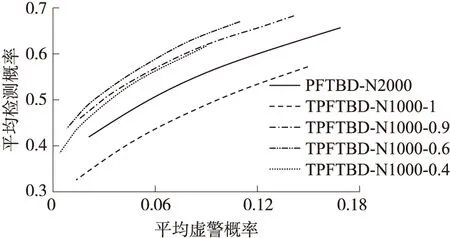
图5 检测性能ROC曲线

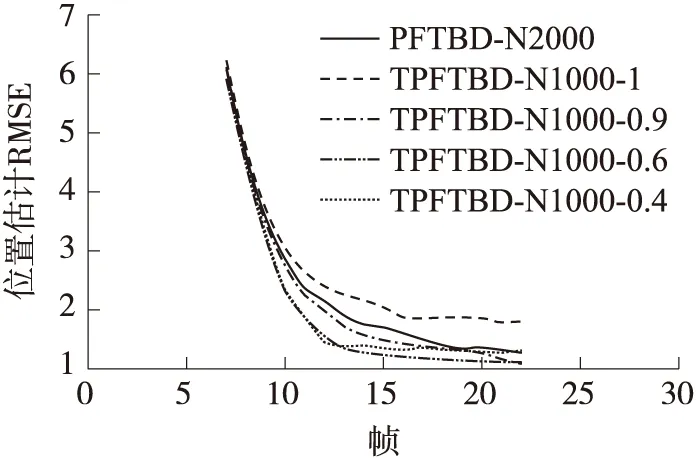
图6 位置估计误差

由图5到图6可以看出,TPFTBD在N=1000下,除了选择ζ=0.4时,性能差于原PFTBD算法在N=2000下的性能外,其他情形下的性能都优于在N=2 000下的PFTBD算法。对于TPFTBD在其他转移参数ζ下的性能,ζ=0.6时略优于ζ=0.9的情形,而更多实验可以证实ζ≤0.5的性能也逐渐下降,这与前面的定性分析基本吻合,所以对于TPFTBD算法中可以选择0.5<ζ<1,特别地可以选择ζ=0.6。在以后的研究中可以考虑采取某种依据后验分布的一些特性的最优或自适应参数选择。

4 总结和展望

针对基于粒子滤波的弱目标检测与跟踪问题,提出了一种基于两级量测更新的TPFTBD算法。该方法在PF状态估计完成之后,利用其估计信息进行了某种量测信息的二次更新处理,提高了粒子携带信息的利用程度,最终改善了检测与估计性能。该算法还可以在Salmond的PFTBD架构下实现,或结合PF其他变种进一步提升性能。未来的研究将包括多目标、多传感器TBD问题以及多种TBD方法的综合等。

[1]Ristic B,Arulampalam S,Gordon N.Beyond the Kalman Filter:Particle filters for Tracking Applications[M].Boston-London:Artech House,2004:239-259.

[2]Salmond D J,Birch H.A Particle Filter for Track-before-Detect[C]//Proc of American Control Conference,Arlington,June 25-27,2001:3755-3760.

[3]Boers Y,Driessen J N.Particle Filter Based Detection for Tracking[C]//Proc of American Control Conference,Arlington,June 25-27,2001:4393-4397.

[4]Rutten M G,Gordon N J,Maskell S.Particle-Based Track-before-Detect in Rayleigh Noise[C]//Proc of Signal and Data Processing of Small Targets,Orlando FL,April 13-15,2004,5428:509-519.

[5]Rutten M G,Ristic B,Gordon N J.A Comparison of Particle Filters for Recursive Track before Detect[C]//Proc of the 8th International Conference on Information Fusion(FUSION2005),Piscataway:IEEE Press,2005:169-175.

[6]Maskell S R,Weekes K R,Briers M.Distributed Tracking of Stealthy Targets Using Particle Filters[C]//Proc of IEE Seminar on Target Tracking:Algorithms and Applications,Birmingham,UK,May 7-8,2006:11-20.

[7]Hlinomaz Peter,Hong Lang.A Multi-Rate Multiple Model Track before Detect Particle Filter[J].Mathematical and Computer Modeling,2009,49:146-162.

[8]龚亚信,杨宏文,胡卫东,等.基于粒子滤波的弱目标检测前跟踪算法[J].系统工程与电子技术,2007,29(12):2143-2148.

[9]胡洪涛,敬忠良,胡士强.基于辅助粒子滤波的红外小目标检测前跟踪算法[J].控制与决策,2005,20(11):1208-1211.

[10]赵志国,王首勇,同伟.基于重采样平滑粒子滤波的检测前跟踪[J].空军雷达学院学报,2008,22(1):25-28.

[11]Su H T,Wu T P,Liu H W,et al.Rao-Blackwellised Particle Filter Based Track before Detect Algorithm[J].IET Signal Processing,2008,2(2):169-176.

[12]Li Cuiyun,Ji Hongbing.Marginalized Particle Filter Based Track-before-Detect Algorithm for Small Dim Infrared Target[C]//Proc of the 2009 International Conference on Artificial Intelligence and Computational Intelligence.Shanghai,China,November 7-8,Vol.3,321-325.

[13]吴孙勇,廖桂生,杨志伟,等.粒子滤波的检测前跟踪改进算法[J].控制与决策,2010,25(12):1843-1847.

[14]Wu Z,Su T.Radar Target Detect Using Particle Filter[C]//Proc of IEEE International Radar Conference 2010,Washington DC,United states,May 10-14,2010:955-958.

[15]梁新华,潘泉,杨峰,等.基于两级采样的粒子滤波检测前跟踪算法[J].系统工程与电子技术,2011(9):1921-1926.

[16]梁新华,梁彦,潘泉,等.一种基于局部搜索采样的粒子滤波检测前跟踪算法[J].控制与决策,2012(12):1912-1916.

[17]Punithakumar K,Kirubarajan T,Sinha A.A Sequential Monte Carlo Probability Hypothesis Density Algorithm for Multitarget Track-before-Detect[C]//Proc of SPIE-Signal and Data Processing of Small Targets 2005,San Diego,CA,United States.International Society for Optical Engineering,Bellingham WA,United States,2005:1-8.

[18]童慧思,张颢,孟华东,等.PHD滤波器在多目标检测前跟踪中的应用[J].电子学报,2011,39(9):2046-2051.

[19]Huisi T,Hao Z,Huadong M,et al.Multitarget Tracking Before Detection via Probability Hypothesis Density Filter[C]//Proc of International Conference on Electrical and Control Engineering,ICECE 2010,2010:1332-1335.

[20]Tong H,Zhang H,Meng H,et al.A Shrinkage Probability Hypothesis Density Filter for Multitarget Tracking[J].EURASIP Journal on Advances in Signal Processing,2011(1):1-13.

[21]林再平,周一宇,安玮,等.基于概率假设密度滤波平滑器的检测前跟踪算法[J].光学学报,2012,32(10):132-139.

[22]林再平,周一宇,安玮.改进的概率假设密度滤波多目标检测前跟踪算法[J].红外与毫米波学报,2012,31(5):475-480.

[23]Ba-Ngu V,Ba-Tuong V,Nam-Trung P,et al.Joint Detection and Estimation of Multiple Objects from Image Observations[J].IEEE Transactions on Signal Processing,2010,58(10):5129-5141.

[24]胡振涛,潘泉,杨峰.基于广义UT变换的交互式多模型粒子滤波算法[J].电子学报,2010,38(6):1443-1448.

A Particle Filter Track-Before-Detect Algorithm Based on Two-Stage Measurement Update*

CHENYanjun1*,LIANGXinhua2,PANQuan2,LIANGYan2

(1.Key Laboratory of Photo Electricity Gas and Oil Logging and Detecting of Ministry of Education,Xi’an Shiyou University,Xi’an 710072,China;2.Institute of Control and Information,School of Automation,Northwestern Polytechnical University,Xi’an 710065,China)

A particle filter track-before-detect algorithm based on two-stage measurement update was proposed,to deal with detection and tracking a dim target in low signal-to-noise ratio.After updating of the posterior state in particle filter,by using Kalman filter,a second-stage measurement update is executed.This improves the degree of using of particles-contained information.Simulation results show that the new algorithm obtains better detection and tracking performance.

dim target;track-before-detect;particle filter;two-stage measurement update

陈延军(1977-),男,河南焦作孟州市人,1994～1998年毕业于中国地质大学(武汉)应用地球物理专业;1998～2003年工作于东方地球物理公司,主要从事地震资料数据处理方法研究。2003～2011年西北工业大学完成硕博士阶段学习,专业分别是机械电子工程、控制科学与工程。2012年入职西安石油大学电子工程学院,目前主要研究领域为信息融合、分布式估计与控制,allexist@126.com;

梁新华(1976-),男,山西河曲人,博士研究生,主要研究领域为目标检测与跟踪、信息融合等,plowliang@gmail.com。

潘 泉(1961-),男,上海人,教授,博导,博士,主要研究领域为动态系统建模、多目标跟踪与识别、信息融合等;

项目来源:国家自然科学基金重点项目(41474108,61135001)

2014-07-01 修改日期:2014-11-12

C:7230

10.3969/j.issn.1004-1699.2015.01.020

TP391

A

1004-1699(2015)01-0115-06