基于DFT的相位差估计精度与改进方法*
杨辉跃,涂亚庆,张海涛
(后勤工程学院信息工程系,重庆 401311)
基于DFT的相位差估计精度与改进方法*
杨辉跃,涂亚庆*,张海涛
(后勤工程学院信息工程系,重庆 401311)
相位差是传感器信号处理中重要的检测参数。针对相位差高精度估计要求,在阐述DFT相位差估计原理基础上,分析了影响估计精度的主要因素,推导出估计方差与信噪比、采样长度、频率偏差及对称窗型窗长的具体关系,并给出了满足精度要求的信噪比、采样长度和和频率偏差条件。提出一种校正谱泄漏的相位差估计方法,先通过比值法计算出频率偏差,然后考虑负频率泄漏影响进行相位差估计,校正了短程和长程两类谱泄漏影响,给出了加矩形窗或Hanning窗的估计式和方法步骤。实验结果验证了估计精度分析及本文方法性能,科氏流量计应用实验表明了方法的工程可行性和实用价值。
离散傅里叶变换;相位差估计;频谱泄漏;负频率
相位差估计技术在传感器信号处理、仪器仪表、故障诊断、电力电子等诸多领域有着广泛且重要的应用[1-5]。实际应用中对相位差估计精度有较高的要求,例如,对称负载下同步发电机三相输出电压之间的相位差在±0.6°范围内,正常情况下电容型高压电气设备的介质损耗角小于0.1°。因此,分析影响相位差估计精度的主要因素,实现对相位差高精度估计具有重要的现实意义和应用价值。
目前针对相位差估计,已提出多种估计方法,它们有各自的优缺点和适用范围。基于硬件电路的过零检测法[6]根据两路信号过零点时间计算相位差,计算速度快,但硬件成本高、抗干扰能力弱;数字相关法[7]利用两路信号的相关函数估计相位差,对随机噪声抑制能力强,但受谐波影响较大且要求整周期采样;高阶谱和互高阶谱估计法[8]基于信号高阶谱估计相位差,算法复杂,计算量大;Hilbert变换法[9]先对信号进行90°移相,然后利用两路信号移相前后的函数关系计算相位差,可动态估计时变相位差,但易受谐波干扰。DFT相位差估计通过信号离散频谱最大谱线处的相位相减获得相位差,估计精度相对较高,可利用FFT快速算法,实时性强且便于硬件实现,应用广泛。然而,DFT计算过程中的频谱泄漏会影响相位差估计精度[10-12]。
本文在分析DFT相位差估计精度基础上,提出一种校正谱泄漏的相位差估计方法。该方法首先通过比值法计算出频率偏差,然后考虑负频率泄漏影响,校正短程和长程两类谱泄漏[13-14]估计相位差,具有较高精度,其有效性和估计性能将在对比实验中进行验证。
1 加窗DFT相位差估计原理
设2路单频信号为s1(n)、s2(n),f0表示频率,幅值和初始相位分别为A1、A2和θ1、θ2,以频率fs(fs>2f0)对s1(n)和s2(n)进行离散采样,并用长度为N的离散对称窗w(n)进行截短,得到有限长离散加窗采样序列:
s1w(n)=A1cos(2πf0n/fs+θ1)w(n)s2w(n)=A2cos(2πf0n/fs+θ2)w(n)
(1)
先估计相位θ1。对s1w(n)进行DFT,得离散频谱
(2)
忽略负频率成分,在非整周期截断时,即N≠mfs/f0,m∈Z+,频谱泄漏存在频率估计偏差δ,|δ|≤0.5。从而,可设f0=(k+δ)Δf,k为正整数,Δf为频率分辨率,则:
(3)
从而,s1w(n)的相位为:φ1=θ1+πδ。同理可得s2w(n)的相位:φ2=θ2+πδ。则估计相位差为:
(4)
2 估计精度分析
2.1 估计方差
在加性噪声背景下,用长度为N对称窗wN(n)对含噪观测信号x(n)进行加窗截短,得:
xw(n)=x(n)wN(n)+z(n)wN(n)
(5)
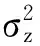
对xw(k)进行DFT,忽略负频率成分,只考虑DFT频谱的前N/2点,有
(6)
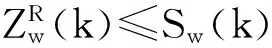
(7)
利用二阶泰勒公式展开,忽略高阶无穷小,得:
(8)
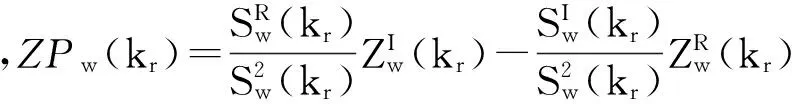
设Pw为窗的平均功率,对噪声谱有
(9)
由于高斯白噪声任意两条谱线的实部和虚部相互独立,则
(10)
从而,根据信噪比定义和对称窗频谱,可得相位谱均值和方差
(11)
(12)
可见,相位差估计精度与信噪比、频率偏差、所加对称窗形状和长度有关。
2.2 满足精度要求的估计条件
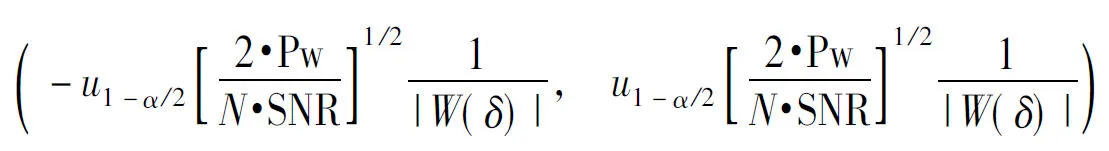
(13)
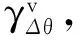
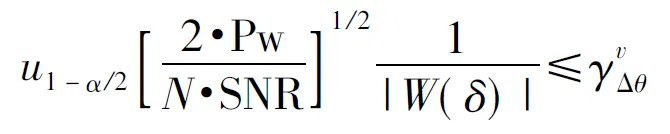
(14)
整理得:
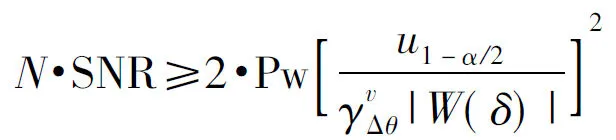
(15)
上式即为满足精度要求的DFT相位差估计条件。
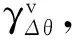
(16)
由式(16)即可求得频偏δ的取值范围。
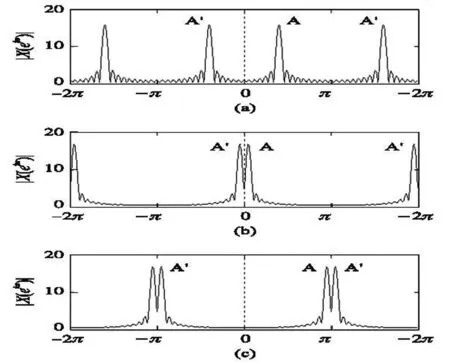
图1 单频信号负频率泄漏
2.3 负频率泄漏影响
上述相位差估计原理忽略了负频率成分的影响,然而研究表明当信号频率很低或接近Nyquist频率时,由于频谱泄漏导致负频率谱峰叠加到正频率谱,造成负频率干涉影响相位差估计精度。如图1所示,信号频率在(0,π)的正频率区间,(-π,0)和(π,2π)是正频率区间关于ω=0和ω=π的对称频谱镜像,称为负频率区间。当信号频率较低或接近Nyquist频率时,谱峰A靠近(0,π)两端,旁瓣干涉迅速增大,甚至造成主瓣干涉,如图1(b)和图1(c)所示。此时考虑负频率泄漏的影响十分必要。
3 校正方法
3.1 基本思想
根据上述分析,基于DFT的相位差估计精度与信噪比、频率偏差、窗长和窗形以及负频率泄漏有关。因此,当信噪比一定时,可先进行比值法获得频率偏差,然后不忽略负频率成分计算相位差,从而实现相位差估计校正,改善估计精度。
3.2 方法原理
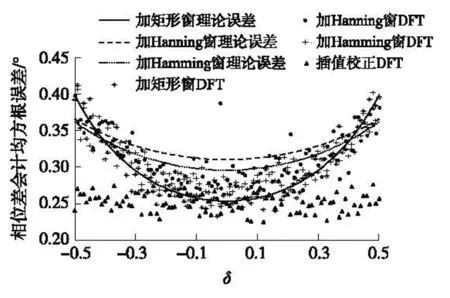
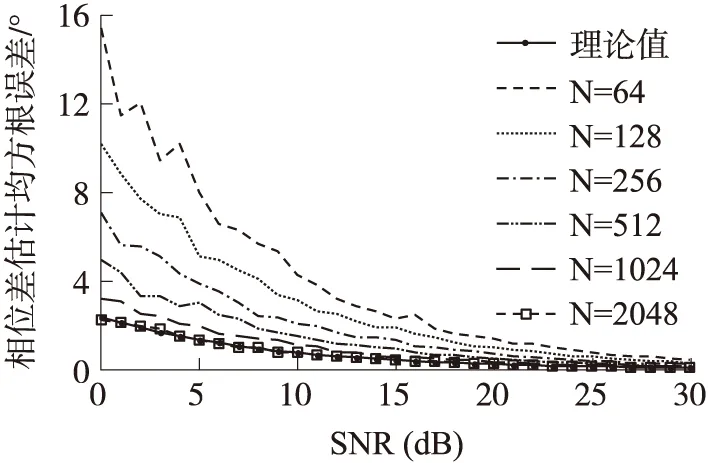
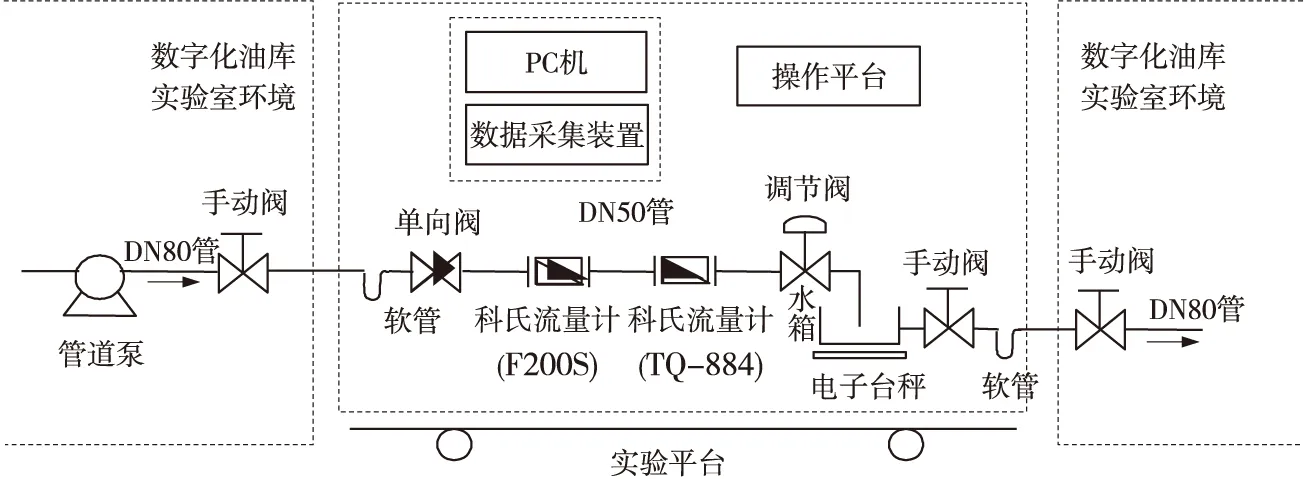
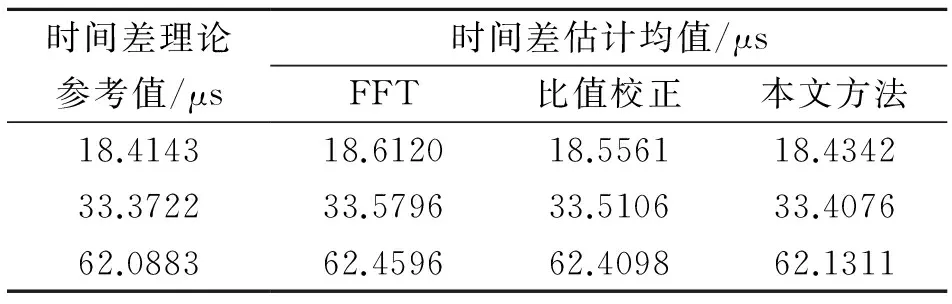
为获得频率偏差δ,本为采用比值法[15]即利用主瓣内最大谱线和次大谱线的幅值谱之比进行求解。设最大谱线和次大谱线分别为yk和yk+1,对应相位为θk和θk+1,则有k v=yk/yk+1=W(δ)/W(1+δ) (17) 将所加窗函数频谱代入式(14),利用峰值搜索或牛顿迭代法,即可求得频率偏差δ。 若||θk-θk+1|-π|>ε,则认为存在谱线干涉[16]。此时,负频率成分不可忽略。根据式(2),在不忽略负频率的情况下重新推导相位差估计公式。若所加对称窗为矩形窗,则经推导后可得[17] (18) 式中,φ1为S1(k0)的相位,c1=sin(2πk0/N);c2=sin[2π(k0+δ)/N];c3=2sin(πδ/N)sin[π(2k0+δ)/N]。 同理,对于第2路正弦采样序列s2(n),有: (19) 式中,φ2为S2(k0)的相位。由式(18)和(19),可求得相位差: (20) 若所加窗为Hanning窗,同理可推导出校正后的相位差: (21) D1=1+cos(2π/N)- 2cos(πδ/N)cos[π(2k0+δ)/N]cos(2πk0/N) D2=1+cos(2π/N)- 2cos(πδ/N)cos[π(2k0+δ)/N]cos[2π(k0+δ)/N] 3.3 方法步骤 方法实现步骤如下: Step 1 加窗截短,用长度为N对称窗wN(n)对采样信号x(n)进行加窗截短; Step 2 频谱分析,对截取的信号进行DFT计算,获得信号离散频谱; Step 3 频偏计算,根据信号离散频谱,利用比值法,通过峰值搜索计算出频偏δ; Step 4 相位差估计,根据窗wN(n)形状选择式对应的(20)或式(21)估计相位差。 采用单频实正弦信号迭加高斯白噪声,对本文理论推导进行验证。两路信号所加噪声互不相关,分别对频偏、信噪比和采样长度、对称窗型进行单因素分析,并对比本文方法与原方法性能,给出精度要求下的估计条件。实验中,两路单频实正弦信号初始相位差Δθ=3.6°。 4.1 频偏δ与窗函数的影响分析 在信号频率f0=200 Hz,SNR=20 dB条件下,分别用矩形窗、Hanning窗、Hamming窗截取N=1 024点数据,经DFT估计信号相位差。同时采比值法校正后的相位差估计值作为比较,进行200次独立仿真实验,得到相位差估计的均方根误差与频偏δ的关系如图2所示。 图2 频偏δ与窗函数对估计精度的影响 图2中3条线为按式(15)得出的均方误差理论值,离散点为仿真结果。从图2可以看出,仿真结果与理论值基本吻合。未经校正的情况下,频偏|δ|越接近零,即短程谱泄漏越小,DFT法相位差估计的均方根误差越小。对比加不同窗的结果可知,加Hanning窗和加Hamming窗的均方误差相差不大,|δ|较小时,加矩形窗效果较好,当|δ|较大时,加Hanning窗和加Hamming窗的误差更小。比值校正后,均方根误差始终在某定值附近波动,与δ无关。该定值由信噪比和采样长度决定,在本实验给定条件下,该值约为0.253°。 4.2 信噪比与采样长度的影响分析 图3为N=1 024,k0=200,δ=0.4条件下,校正后相位差估计均方根误差与SNR的关系以及在k0=30,δ=0.4,SNR=20 dB条件下,校正后相位差估计均方根误差与采样序列长度N的关系。从图3可以看出,仿真结果与公式计算结果是吻合的,且SNR越高或N越大,相位差估计的均方根误差越小。 图3 信噪比SNR与采样长度对估计精度的影响 4.3 负频率泄漏影响分析 考虑频率较低时负频率泄漏的影响。对2路单频正弦信号,分别用矩形窗和Hanning窗截取N=1 024点,采样频率fs=1 000 Hz,则频率分辨率Δf=fs/N=0.976 6 Hz。为更准确地反映频谱的内在规律,以频率分辨率为单位刻画信号频率,即f0在(0.5~2.5)Δf和(497.5~499.5)Δf内取值,步长为0.05Δf,仿真实验得到相位差估计的相对误差与信号频率的关系,如图4所示。 图4 相位差估计相对误差 从图中可以看出,式(20)和式(21)所示的负频率修正DFT具有更高的估计精度,当相对频率f0/fd为整数时,DFT法的误差急剧下降,接近双精度运算的下限。这是因为当f0等于fd的整数倍时,负频率区间的谱峰A′的旁瓣在正频率区间的谱峰A处的值正好为零,谱峰A并未受到任何影响。 4.4 满足一定精度的估计条件计算 取α=0.01,查正态分布得u1-α/2=2.58,代入式(15)得误差率以99%的概率落在20%内的条件: N·SNR≥166.41·Pw/|W(δ)|2 (22) 科氏流量计通过检测两路振动信号的时间差(相位差)测量质量流量,将本文方法用于科氏流量计进行应用验证。所用实验平台如图5所示,以10 kHz的采样频率,实际采集频率约为146 Hz的流量计振动信号,分别用FFT法、比值校正DFT和本文方法(Hanning窗)进行相位差估计,每次计算64个采样点,所得结果换算成时间差如表1所示。其中理论参考值根据流量计性能曲线由实际流量换算而来。 图5 科氏流量计实验平台 表1 时间差估计值 对比可见,FFT法、比值校正DFT和本文方法估计精度依次提高,其中本文方法计算结果与理论参考值最为接近,验证了校正后的DFT相位差估计能有效抑制频谱泄漏,较大幅度提高估计精度。 针对基于DFT的相位差估计,推导出估计方差表达式,并论述了满足一定精度要求的估计条件,在此基础上,提出一种校正了频谱泄漏的相位差估计方法,给出了方法原理和步骤,实验验证了估计精度分析的正确性以及本文方法的高精度性能,并在科氏流量计中进行了应用实验表明了本文方法可行性和价值。进一步研究将基于本文方法,探讨时变相位差的自适应估计问题。 [1]Liu Xiao,Li Haisen,Zhou Tian.A 3-Subarray DOA Estimation Method Based on Phase Difference Measurement for Multi-Beam Bathymetry Sonar[J].Energy Procedia,2011(13):7683-7689. [2]温和,滕召胜,曾博,等.基于泄漏对消的电力谐波相角高精度估计算法[J].仪器仪表学报,2009,30(11):2354-2360. [3]杨辉跃,涂亚庆,张海涛,等.一种基于SVD和Hilbert变换的科氏流量计相位差测量方法[J].仪器仪表学报,2012,33(9):2101-2107. [4]伯恩,段发阶,吕昌荣,等.基于CORDIC的交流相位跟踪零差补偿方法及其实现[J].传感技术学报,2014,27(2):198-203. [5]冯文光,刘诗斌,李菊萍.数字磁通门传感器的自动相位对准[J].传感技术学报,2012,25(2):212-214. [6]龚国良,鲁华祥.一种利用固定相移测量同频正弦信号相位差的方法[J].仪器仪表学报,2010,31(4):873-877. [7]杨俊,武奇生,孙宏琪.基于相关法的相位差检测方法在科氏质量流量计中的应用研究[J].传感技术学报,2007,20(1):138-145. [8]宁辉.噪声背景下正弦信号相位估计的互高阶谱方法[D].长春:吉林大学,2001. [10]张海涛,涂亚庆,牛鹏辉.相位差测量的FFT法和DTFT法误差分析[J].电子测量与仪器学报,2007,21(3):61-65. [11]李炯,王岩飞.DFT相位估计算法及噪声敏感频率问题分析[J].电子与信息学报,2009,31(9):2101-2103. [12]Schuster S,Scheiblhofer S,Andreas S.The Influence of Windowing on Bias and Variance of DFT-Based Frequency and Phase Estimation[J].IEEE Transactions on Instrumentation and Measurement,2009,58(6):1975-1990. [13]Young S S,Ho K J,Weui B W,et al.A Study on the Leakage Error in the Spectrum of Acoustic Intensity[J].JSME International Journal Series A,2004,47(1):42-46. [14]刁瑞朋,孟庆丰.基于长程泄漏补偿的迭代插值FFT方法及应用[J].振动与冲击,2013,32(22):1-6. [15]丁康,谢明,杨志坚.离散频谱分析校正理论与技术[M].北京:科学出版社,2008. [16]谢明,丁康,莫克斌.频谱校正时谱线干涉的影响及判定方法[J].振动工程学报,1998,11(1):52-57. [17]Tu Yaqing,Zhang Haitao,Mao Yuwen,et al.Unbiased Phase Delay Estimator with Negative Frequency Contribution for Real Sinusoids[J].Journal of Applied Sciences,2013,13(8):1160-1168. Precision Analysis and Improvement Method for DFT Based Phase Difference Estimation* YANGHuiyue,TUYaqing*,ZHANGHaitao (Department of Information Engineer,Logistical Engineering University,Chongqing 401311,China) Phase difference is an important parameter waiting for estimation in sensor signal processing.To fulfill precision requirements,effects against DFT based phase difference measurement method are analyzed on top of its measurement principle introduction.We derived the relationship between estimated variance with SNR,sampling length,frequency deviation,types and length of symmetrical window.Requirements for SNR,sampling length and frequency deviation are also put forward.In succession,a new phase difference measurement method with spectrum leakage revised is proposed.In the method,frequency deviation is firstly calculated by interpolation algorithm,and then phase difference is computed with the negative frequency influence considered.The short-range and long-range spectrum leakages are both taken into consideration in this method.Procedures and formulas for phase difference computation with rectangular window and Hanning window are given out.Experimental results prove the validity of precision analysis.Good performance in precision of the proposed method is also verified.Feasibility and practical value of the proposed method is shown by application experiments in Coriolis mass flow meter. discrete Fourier transform;phase difference estimation;spectrum leakage;negative frequency 杨辉跃(1987-),男,湖南邵阳人,博士研究生,主要研究方向为智能检测与智能控制,数字信号处理,huiyue_yang@163.com; 涂亚庆(1963-),男,重庆人,教授,博士,博导,主要研究方向为智能检测与智能控制,智能自动化系统,数字信号处理,yq.tu@163.com。 项目来源:国家自然科学基金项目(61271449,61302175);重庆市自然科学基金项目(CSTC2012jjA040006,CSTC2013jcyjA40030) 2014-10-08 修改日期:2014-11-15 C:7230 10.3969/j.issn.1004-1699.2015.01.017 TN911.7 A 1004-1699(2015)01-0093-06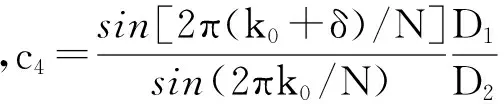
4 实验分析

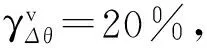
5 应用验证
6 结束语


- 传感技术学报的其它文章
- 基于两步前向区域空洞预测的WMSNs路由算法

