基于角位置的弹载捷联稳定系统设计

高 鹏

(中国空空导弹研究院，河南 洛阳 471009)

【装备理论与装备技术】

基于角位置的弹载捷联稳定系统设计

高 鹏

(中国空空导弹研究院，河南 洛阳 471009)

以某型弹载天线伺服系统为对象，建立了基于DSP的角位置补偿捷联稳定平台硬件系统，推导了捷联稳定的实现算法，并基于Matlab软件仿真分析，分析了对稳定系统去耦能力影响的重要参数，对其稳定性能进行了试验验证，并给出了改善系统性能的改进方向。

捷联稳定系统 ；DSP；去耦能力

在运动载体上对目标进行跟踪和测量的雷达系统，视线稳定是实现可靠、高精度跟踪的基础，为了消除载体扰动的影响，通常采用稳定平台来实现视线稳定[1]。目前，稳定平台通常是将陀螺仪直接安装在天线伺服框架上，测量信息直接反馈，从而隔离载体扰动的影响。但是，随着高精度、小型化导引头的发展需要，直接采用陀螺稳定天线的技术受到限制，为此提出采用捷联稳定方式来解决天线稳定问题[2]。由于弹上天线稳定系统的特殊性，如动态响应快和比较严格的体积限制，这就对弹上导引头捷联稳定方式提出更高的要求[3]。

本研究基于Matlab软件的进行了仿真分析，并建立了基于DSP捷联稳定平台系统，通过摇摆台试验，验证了稳定算法的正确性，并且在此基础上进行了两项参数对稳定性能的影响分析，得出了改进角位置捷联式天线稳定平台的方向。

1 捷联稳定系统控制方案

1.1 捷联稳定系统原理与组成

捷联天线稳定系统的原理框图如图1所示，其中角度传感器敏感天线框架角运动，捷联惯导敏感弹体姿态运动，这些信息同时送给DSP，完成角位置捷联稳定算法、角位置预定回路校正网络及伺服系统控制量的计算，再通过功率放大带动天线伺服机构。

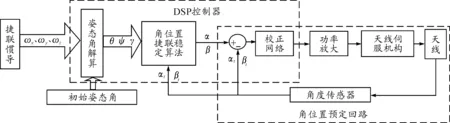
图1 捷联稳定平台的原理框图

图1中，速率陀螺输出通过串口输出弹体角速率ωx、ωy、ωz，DSP控制器通过串口接收3个角速率，并通过姿态角解算算法得出弹体实时姿态角θ、φ、γ，并通过AD采集天线伺服框架上的角度传感器信息αt、βt，再通过捷联稳定算法得到天线实时的指向角α、β，与天线角度传感器的反馈αt、βt形成误差信号，经过校正后得到输出电压并通过PWM功率放大驱动天线伺服机构，通过执行环节驱动天线转动，最终使天线保持在惯性空间的稳定。

1.2 算法设计

1.2.1 坐标定义

本系统的坐标定义以及坐标变换关系：弹体坐标系(OmXmYmZm)：弹体坐标系原点在导弹的质心上，Xm为导弹的指向头部为正，Ym轴和Zm轴位于导弹的翼面所在的平面内，构成右手坐标系。弹体坐标系是在惯性坐标系的基础上先绕Y轴旋转偏航角φ，到达OmX1Y1Z1，再绕Z1轴旋转俯仰角θ，到达OmX2Y2Z2，然后绕X2轴旋转横滚角γ得到。

天线坐标系(OaXaYaZa)：导引头天线坐标系的初始位置与弹体坐标系平行，原点位于天线的回转中心，导引头天线首先绕OmXm轴旋转45°,得到OaXcYcZc，然后绕OaYc轴旋转α角(偏航)，得到OaXbYbZb，最后绕OaZb轴旋转β角(俯仰)得到天线坐标系。图2所示为各坐标系的关系。

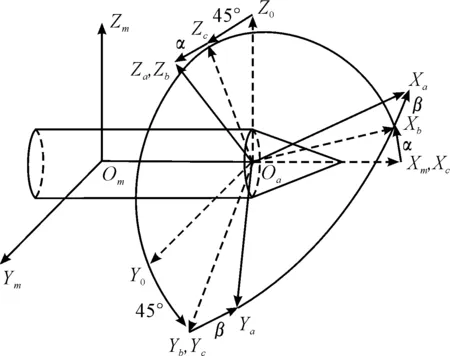
图2 各坐标系关系

1.2.2 姿态角解算算法设计

由于稳定系统是一个实时性很强的系统，因此，如何通过陀螺输出的3个角速率快速准确解算实时姿态角，是姿态角解算算法的难点，为此本研究采用了增量矩阵积分算法来实现[4]。

初始时刻姿态矩阵AIR根据姿态角计算

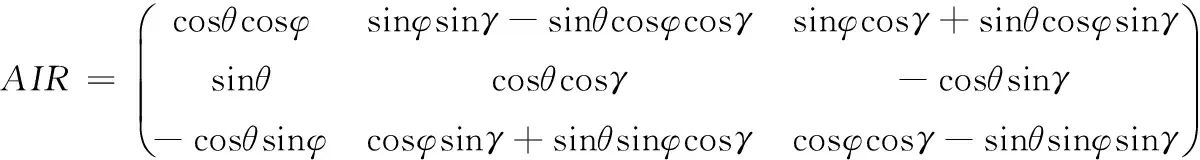
(1)

式中：θ为俯仰角；φ为偏航角；γ为滚转角。之后，姿态矩阵AIR根据角速度进行更新。设已知t时刻姿态矩阵为AIR(t)，角速度为ω=(ωx，ωy，ωz)T。则t+Δt时刻，实时姿态矩阵AIR(t+Δt)计算方法如下：

u={ωx，ωy，ωz}TΔt

则有

AIR(t+Δt)=AIR(t)·dc

(2)

1.2.3 天线的角位置稳定原理[5-6]

天线数字稳定原理是利用天线波束指向在惯性空间的不变原理，设计数字转化平台，使天线最大波束指向在惯性空间指向不变。若在n-1采样时刻，天线坐标系的纵轴上有单位矢量，即在主波束方向上的单位矢量[1,0,0]T，则有

(3)

式中，φn-1、θn-1、γn-1分别为n-1采样时刻弹体姿态的偏航角、俯仰角、滚转角，均由陀螺角速率积分得到。αn-1和βn-1为n-1采样时刻天线的偏航角和俯仰角。天线在n-1采样时刻在惯性空间的指向[xn-1yn-1zn-1]T可由式(3)求得。

n采样时刻天线实时指向[xnynzn]T保持在惯性空间不变，即：

(4)

(5)

实时的弹体姿态角(φn-1、θn-1、γn-1)由角速率积分得出，解式(4)，可求得所需的αn和βn，即天线相对于弹体的转角，与上一时刻的天线转角αn-1和βn-1相减，可得相对转动量Δα和Δβ，则可抵消弹体扰动对天线指向的影响，从而保证天线在惯性空间指向不变。可见式(4)就是天线的数字稳定矩阵。

实际上，对M、K、L矩阵，其逆矩阵等于其转置矩阵，由于三角函数的特殊性，且等于反向旋转相同的角度，则式(4)的计算可以简化为

(6)

简化为

(7)

因天线转角α和β均在-π/2～π/2间变化，从而可以求出

(8)

由式(8)进行迭代，即可得到弹体扰动的实时天线转角指令信号为

Δαn=αn-αn-1， Δβn=βn-βn-1

(9)

2 系统仿真与测试

本章将建立捷联稳定平台系统仿真模型，并分析捷联惯导输出弹体姿态角速率的周期对本系统去耦能力的影响，以及角位置预定回路增益对本系统去耦能力的影响。去耦能力是捷联稳定平台抗弹体扰动对天线指向影响的指标，是捷联稳定系统最重要的一个指标，去耦能力的计算是天线指向的幅度与弹体扰动幅度的比值，比值越小去耦能力越强。

2.1 捷联稳定仿真模型

根据1.1节的系统组成建立捷联稳定平台系统仿真模型。如图3所示，模型中包括姿态角解算算法、角位置捷联去耦算法[7-8]及平台角位置预定回路仿真模型[9-13]。姿态角解算根据初始姿态角及弹体姿态角速率(ωx，ωy，ωz)解算出姿态矩阵，角位置捷联去耦模块根据姿态矩阵及平台框架角(αn-1，βn-1)解算出(αn，βn)，把计算结果输出到角位置预定回路输入端，并建立稳定平台伺服控制系统模型，包括校正环节，各个比例放大环节以及电机模型等。

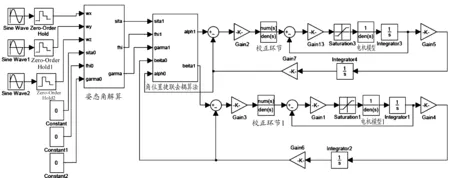
图3 捷联稳定系统仿真模型

2.2 捷联惯导数据更新周期对去耦性能影响

根据图3所示捷联稳定系统模型，分别对采样保持时间为4，12和24 ms做了对比，选取回路增益为10，仿真时数据采用32位single数据类型，结果如如表1所示。

从仿真结果可以看出捷联惯导数据更新周期对系统去耦性能有显著影响，周期越小，去耦能力越强。

2.3 预定回路增益对去耦结果的影响

分别仿真了预定回路增益为1、10和30做了对比，选取采样保持时间为4 ms确定了回路的幅值裕度和相位裕度、超调以及去耦能力，结果如表2所示。

表1 捷联惯导数据更新周期对去耦性能影响

表2 预定回路增益对去耦结果的影响

从仿真结果可以看出：预定回路增益的变化对去耦能力影响较显著，放大倍数越大，去耦能力越强，但随着放大倍数的增加，系统稳定性变差，表现为相位裕度减小，超调增加。

2.4 测试结果

基于以上建立的捷联稳定系统，本研究对该稳定系统进行了去耦能力的测试，在负载天线上安装了2个光纤陀螺作为测试用传感器，将被测系统安装于摇摆台上，摇摆台以幅度为3°、频率为1Hz进行摇摆，稳定系统数据类型采用32位single数据类型，捷联惯导数据更新周期为4 ms，角位置预定回路增益为10，稳定系统在开环和闭环的2种状态下对光纤陀螺输出进行分析，得到其在1 Hz时的输出幅值Uo(开环幅值)和Uc(闭环幅值)，则去耦能力即为Uc/Uo，如图4所示，按照原频域处理方法得到去耦系数为2.34%。

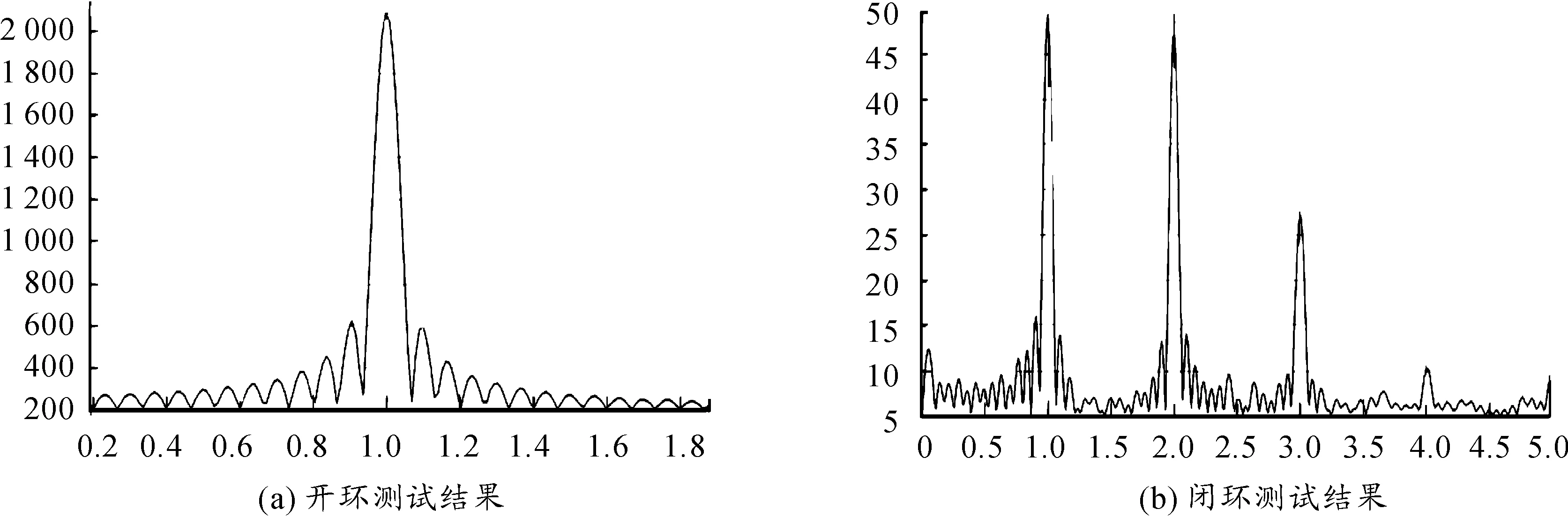
图4 捷联稳定系统摇摆台测试结果

3 结论

本研究推导的捷联稳定算法能够实现天线的稳定功能，且稳定系统中捷联惯导数据更新周期及角位置预定回路增益都会对稳定系统的去耦能力有较大影响。为了提高稳定系统去耦能力，可以从减小捷联惯导数据更新周期和提高角位置传感器的精度两个方面着手。

[1] 董树人,姚兆宁.大型船载测量雷达天线的两轴稳定[J].现代雷达,1997(6):51-54.

[2] RUDIN R T.Strapdown stabilization for imaging seekers[R].AIAA-93-2660,1993:1-10.

[3] KENNEDY P J,KENNEDY R L.Direct versus indirect Line of Sight(LOS) stabilization [J].IEEE Trans on Control System Technology,2003,11(1):3-15.

[4] 周瑞青,吕善伟,刘新华.捷联式天线稳定平台动力学建模与仿真分析[J].北京航空航天大学学报,2005(9):953-957.

[5] 周瑞青,吕善伟,刘新华.捷联式天线平台的稳定性研究[J].北京航空航天大学学报,2003,29(6):509-511.

[6] J.C.Hung.捷联式导航平台[M].北京:科学出版社,1979.

[7] 李秋生.相控阵雷达导引头去耦技术研究[J].制导与引信,2005,26(2):19-21.

[8] 郭金良,张钰,汪连栋.舰载相控阵雷达仿真系统研究与实现[J].系统仿真学报,2010,22(11):2571-2574.

[9] 夏福梯.防空导弹制导雷达伺服系统[M].北京:宇航出版社,1996.

[10]刘广,郑铁生.基于虚拟样机技术的舵系统动力学仿真研究[J].系统仿真学报,2011,23(3):502-505.

[11]薛定宇,陈阳泉.基于Matlab/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.

[12]Xiang G S,Wang X Y.Real-time follow-up head tracking in dynamic complex environments[J].Journal of Shanghai Jiaotong University(Science),2009,14(5):593-599.

[13]吴晓燕,张双选.Matlab 在自动控制中的应用[M].西安:西安电子科技大学出版社,2006.

(责任编辑 周江川)

Design of Angle Compensation Based Strapdown Antenna Stabilization System

GAO Peng

(China Airborne Missile Academy, Luoyang 471009,China)

Based on an antenna servo system, this paper established a control system of angle strapdown antenna platform based on DSP, and deduced arithmetic of strapdown antenna stabilization system, and calculated the stabilization performance of this system. The system was analyzed based on Matlab software emluator, and the influence of parameters was analyzed. Experiment results show good agreement with the analysis results and they are validated to each other, which provides the direction to improve the stabilization performance.

strapdown stabilization system; DSP; decouple ability

2015-02-01

高鹏(1984—)，男，工程师，主要从事天线波束稳定系统设计研究。

10.11809/scbgxb2015.08.010

高鹏.基于角位置的弹载捷联稳定系统设计[J].四川兵工学报，2015(8):36-40.

format:GAO Peng.Design of Angle Compensation Based Strapdown Antenna Stabilization System[J].Journal of Sichuan Ordnance,2015(8):36-40.

TP29；TJ8

A

1006-0707(2015)08-0036-05