应急物流供应链运输调度节点可靠性动态分析

李玉兰，陈锦耀，刘永军

(军事交通学院军事物流系，天津300161)

当重大突发事件发生后，通常需要外界在最短时间内高效可靠地提供大量的应急救援物资，也就是应急物资调度。应急物资调度涉及到的技术问题主要有应急物资需求预测、仓储管理、服务设施优化选址、应急运输调度等关键节点，通称应急物流供应链。由于应急物流供应链的管理环节众多、调度物资种类繁杂、运送形式多样，导致物资调度在发生重大突发事件时可能出现不确定性，因为供应链的放大作用，当其中某一环节出现偏差时，必将对应急物资的成功保障产生极大的影响。一些文献将应急物流供应链系统可靠性定义为:突发性事件发生时，应急物流供应链在规定的时间和条件下，满足应急物流设施需求、配送等的应急能力为系统可靠性，完成系统功能的概率为应急物流供应链系统可靠度。根据应急物流业务的功能和特点，供应链系统可靠性可分为各节点的仓储子系统可靠性、运输子系统可靠性、通信交换子系统可靠性、应急物资生产子系统可靠性等［1］。应急运输调度作为应急供应链中的重要一环，是影响应急物资成功到达的关键因素之一，即为运输子系统。

为使道路交通更为可靠，从经济及社会利益方面得到更大收获，国内外的研究人员对应急运输调度可靠性这一关键节点进行了多方面的研究。如Chen A等［2］研究了物流运输网络可靠性的影响条件及相关因素，认为降低物流能力的冗余程度能够有效提高物流系统的可靠性;朱顺应等［3］研究了网络可靠性计算模型问题;陈艳艳等［4］分析了畅通可靠度问题;侯立文等［5］对路网可靠性的形成和影响因素分别进行了说明，从网络的生存性和有效性两个方面进行了研究。

1 应急物流供应链运输调度节点可靠性指标的提出

在应急物流的运输调配环节中，不确定性是指由于道路损坏、车辆设备损坏、司乘人员意外伤害和交通事故等所导致的不确定性，管理规范一般是确定性因素，与应急运输子系统的可靠性结合紧密的应该是广义可靠性，即包括驾驶人员、道路及交通工具可靠性3个主要评价指标。因此，应急物流供应链运输调度节点可靠性包括运输人员的可靠性、交通工具的可靠性及运输路径的可靠性(如图1所示)。

2 系统基本可靠性计算

根据以上论述，可以对应急物资调度中运输调度节点可靠性评价进行建模分析。应急物流供应链运输调度节点可靠性可简化成链状模型，其中包括人员、交通工具和路网3个串联子系统，而每个串联系统又包括各自相关节点的可靠性。设各个串联子系统的可靠性为Al(l=1，2，…，m)，从而整个系统的可靠性为

子系统中各节点的可靠性也可以用这一公式进行计算，设各子系统中节点的可靠性为Blp(p=1，2，…，n)，从而串联子系统的可靠性为

此外，对于应急救援来说，多一条出救路径则多一条保障，增加了可靠性，因此，并联系统的可靠性为

图1 应急物流供应链运输调度节点可靠性指标

3 应急供应链运输调度节点动态可靠性模型的建立

为实现应急物流供应链运输调度节点可靠性的可行性分析，有利于建立数学模型，通常需要把前述的各项可靠性评价指标根据实际情况进行详细地数据处理，由于篇幅限制，具体数据这里不再列出。

为提高应急物流供应链运输调度节点的可靠性，必须从多方面综合考虑，实现准确性较高的预测分析。常用的预测方法主要有回归分析法、指数平滑法、时间序列法、神经网络模型法和灰色模型法及马尔可夫方法等。综合利用灰色关联法及马尔可夫方法这两种预测方法:一方面，利用GM(1，1)模型使数据序列满足马尔可夫的前提条件，即无后效性和平稳过程等均值特点;另一方面，马尔可夫模型又解决了对随机波动性较大序列的预测问题。这两种预测模型的结合运用将会使应急物流供应链运输调度节点动态可靠性的预测更加准确。

(1)通过GM(1，1)模型建立灰色预测累加数列。设有变量 X(0)={x(0)(q)，q=1，2，…，n}为某路段各可靠性元素一定时期内的非负原始数据，根据灰色模型对X(0)进行一次累加可得

式(1)即为 GM(1，1)模型，其中 a、b为常数，可利用最小二乘法求得。白化微分方程(1)的解为

再进行累减计算，得到原始数列的还原预测值为

(2)马尔可夫预测模型。设当前初始状态为

式中Pij为概率值。当由状态Ei经过k步转移到状态Ej的原始数据个数记为Mij(k)，状态Ei出现的次数记为Mi，则由状态Ei经过k步转移到状态Ej的转移概率为

以^x(k)为基准数据，根据预测对象的具体情况，划分为与^x(k)平行的若干条形区域，每个区域构成一个状态。可以用实际值除以预测值得到的相对值为标准划分状态，表示为

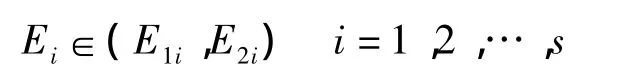
式中:s为划分的状态数目;E1i和E2i分别为第i种状态的上下界。这样就把符合马尔可夫特点的非平稳随机序列X划分为s个状态。划分状态也可利用常数划分法，使样本点相对清楚地划分。

当预测值的变动区间［E1i，E2i］确定后，在上一步得到灰色预测值^x(k)的基础上，根据平行曲线法取区间中值得到马尔可夫预测值Y(k)为

(3)应急物资调度可靠性预测模型。已知上述预测模型及数据组成，则可建立可靠性预测模型。基本过程如下:①根据德尔菲法或专家经验法，分别对参与求助点的参与人员、车辆构成的历年工作可靠性数据进行分析，之后把各出救点与受助点之间的路网划分为单元路径，根据相应要求分别完成道路以季度为单位的可靠性分析;②使用灰色GM(1，1)模型对受助点周边的出救点及单元道路可靠性进行详细计算分析，构成灰色GM预测值;③对灰色GM预测值进行归一化处理并进行状态划分，建立状态转移矩阵，此后利用马尔可夫链完成参与应急物资调度的出救点的路径可靠性预测，之后利用串联公式完成单个出救点到受助点之间的可靠性预测，再利用并联公式完成多个出救点到受助点之间总的系统可靠性预测，从而在要求时间内且物资满足情况下选择最合适的出救点及路径。

4 仿真算例

4.1 问题的提出

设我国境内某山区发生地震等自然灾害，急需物资救助。现有5个出救点，正常情况下从这些出救点调度物资均可在要求时间内到达，但有一定危害性，因此需要详细分析可靠性关系，尽力使可靠性达到80%以上。各出救点人员可靠性和交通工具可靠性相关数据分别见表1和表2，应急路网如图2所示，各单元路径近8个月的可靠性数值见表3。为简单起见，假定每个出救点均能满足物资要求。

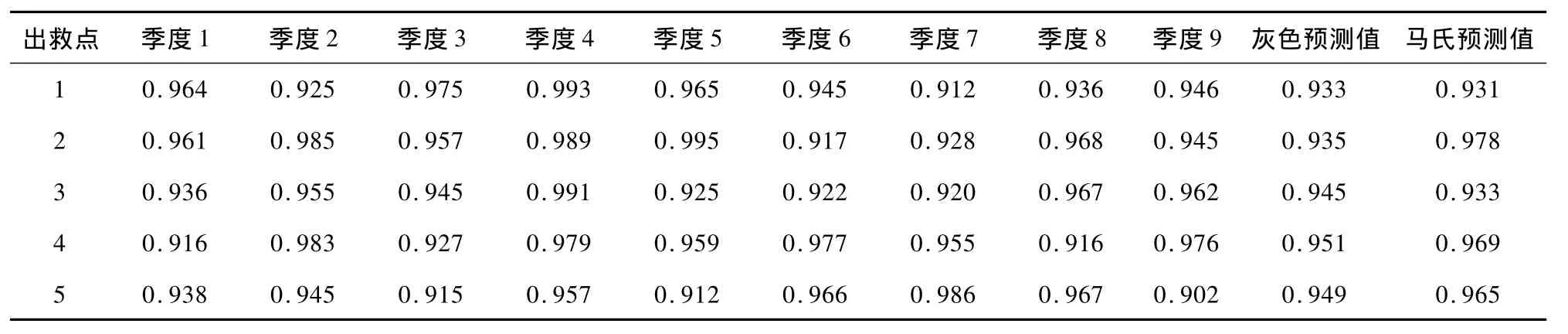
表1 各出救点的人员可靠性数值及预测值

表2 各出救点的交通工具可靠性数值及预测值

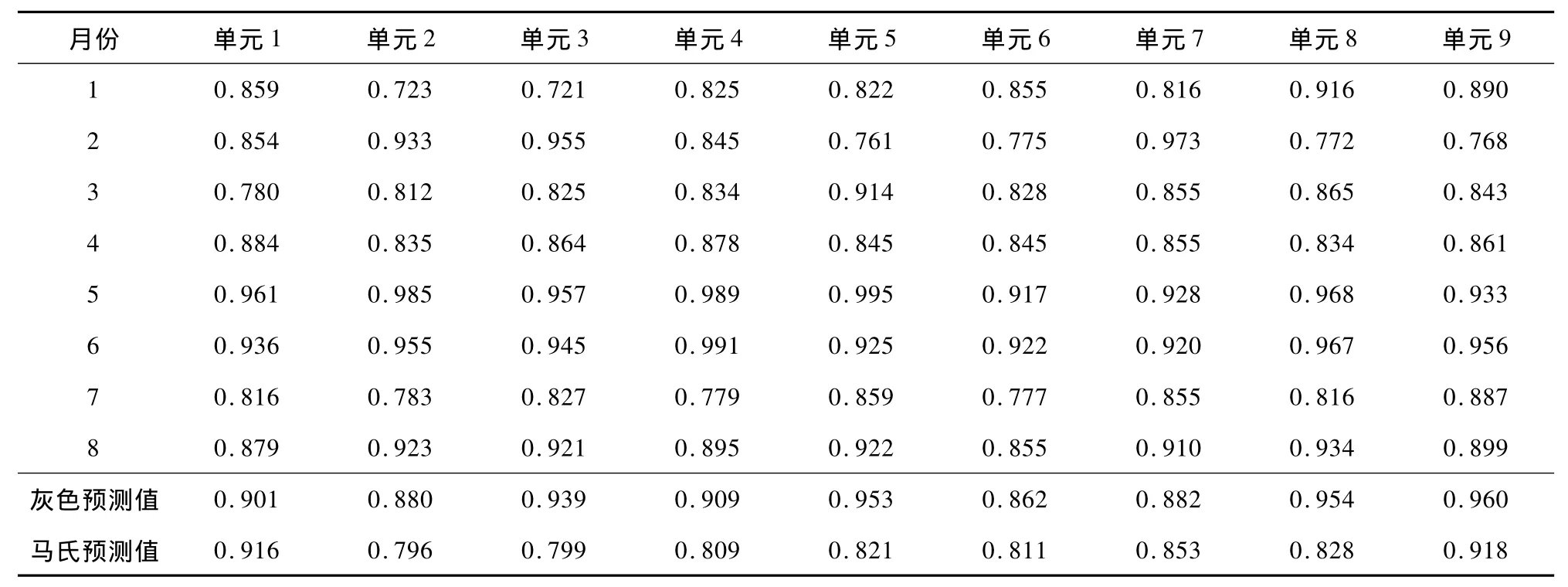
表3 单元路径可靠性数值及预测值

图2 应急路网连接

4.2 灰色GM(1，1)模型预测计算

利用GM(1，1)模型建立基本预测模型，可得各参数当前可靠性预测值，见表1～表3中的灰色预测数据。

4.3 马尔可夫链预测计算

(1)状态区间划分。在得到灰色预测值数据的基础上，先用各出救点的可靠性值与其灰色预测值相比计算出相对值，再利用平行曲线法进行状态划分，分为两个状态区间。如以表1中的出救点1为例，其相对值均值为1.019，状态区间划分为E1(小于均值)和E2(大于均值)(见表4)。

(2)建立转移矩阵。以表4数据为例，根据式(2)，可计算出其一步转移状态矩阵为

由于数据众多，文中不再介绍各转移矩阵。

(3)计算马尔可夫预测值。由表4可知，最后一个数据为1.014，状态为 E1，根据最大概率原则，转为E1状态概率为3/4。由式(3)可得马尔可夫预测值为

4.4 系统可靠性计算

根据图2中的路径连接，以及前述的串联可靠性计算模型，最终可得出各出救点与应急区之间应急调度时的可靠性数值(见表5)。

表4 出救点1的相对值及状态划分

表5 从各出救点到应急地的点对点可靠性数值

如果需要进一步提高可靠性，在尽量节约成本的情况下先选双链应急调度来分析可靠性，显而易见需要选择出救点2和出救点4调度链，其可靠性值为

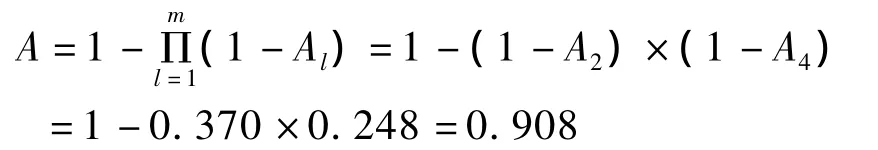
由以上数据可知，已经达到可靠性要求。

5 结语

当突发重大事件发生后，通常需要外界在最短时间内高效可靠地提供大量的救援物资。本文从人员、物资、交通工具、路网等各个物流环节出发，对应急物流供应链运输调度节点可靠性问题进行了研究，提出与军地一体化应急物流结合更为紧密的应该是广义可靠性，即包括驾驶人员、交通工具及运输路径可靠性3个主要评价指标，并在此基础上，综合利用灰色关联法及马尔可夫方法这两种预测方法，建立应急物流供应链运输调度节点可靠性模型，从而得到应急物资调度时运输调度节点的可靠性预测值。由于所计算的数据受到众多因素的影响，计算出的可靠性预测值准确度有限，但通过分析和比较可靠性值的相对大小，可以在时间及运量均满足的条件下，选择可靠性较高的出救点及路径，从而更好地完成应急调度工作。

［1］ 郑哲文.基于可靠技术的应急物流供应链构建［J］.中国流通经济，2009(10):54-56

［2］ Chen A，Yang H，Lo H K，et al.A capacity related reliability for transportation networks［J］.Journal of Advanced Transportation，1999，33(2):183-200.

［3］ 朱顺应，王炜.交通网络可靠度及其通路算法研究［J］.中国公路学报，2000，13(1):92-94.

［4］ 陈艳艳，梁颖，杜华兵.可靠度在路网运营状态评价中的应用［J］.土木工程学报，2003，36(1):36-40.

［5］ 侯立文，蒋馥.城市道路网络可靠性的研究［J］.系统工程，2000，18(5):44-48.