硬件延迟偏差对卫星钟差解算的影响

于合理，郝金明，谢建涛，周 颖，郑国庆

(1.信息工程大学 导航与空天目标工程学院，郑州 450052；2.61287部队，昆明 650102；3.61206部队，北京 100042)

硬件延迟偏差对卫星钟差解算的影响

于合理1，郝金明1，谢建涛1，周 颖2，郑国庆3

(1.信息工程大学 导航与空天目标工程学院，郑州 450052；2.61287部队，昆明 650102；3.61206部队，北京 100042)

接收机接收到的不同类型观测量的硬件延迟存在偏差，给出了利用消电离层组合进行卫星钟差解算时硬件延迟偏差改正的方法，并采集实验数据分析了硬件延迟偏差对卫星钟差解算的影响。实验结果表明：硬件延迟偏差会引起卫星钟差解算结果的系统性偏差，这一系统性偏差与卫星有关，不同卫星的系统性偏差不同，这一偏差可以达到2 ns，应该加以改正。

硬件延迟；消电离层组合；硬件延迟偏差；卫星钟差；系统性偏差

1 引言

精密卫星钟差是采用伪距和相位观测量，利用全球观测站组网求解得到。在广域实时精密单点定位系统中，通常利用全球卫星导航系统国际服务协会(international global navigation satellite system service，IGS)提供的超快速轨道产品和几个区域参考站网络来实时估计卫星钟差[1]。不同类型的观测量的硬件延迟存在偏差，钟差估计过程中很难将硬件延迟与钟差参数分离。文献[2]在比较PANDA 软件计算的精密钟差和IGS 事后精密钟差时，发现两者之间存在一个与卫星相关的系统性偏差，猜测是不同卫星钟的硬件延迟改正不同引起的。IGS公布的精密卫星钟差产品是以双频P码消电离层组合为基准的钟差，但并不是所有的接收机都能提供P1和P2观测量，因此在卫星钟差解算中需要考虑硬件延迟偏差(different code bias，DCB)的影响[3]。本文从观测方程着手分析了硬件延迟偏差的改正方法，通过精密卫星钟差估算软件和观测数据分析了DCB对卫星精密钟差解算结果的影响。

2 硬件延迟偏差改正

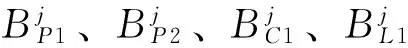
(1)

(2)

根据消电离层组合系数可以得到

(3)

采用上式进行卫星钟差估计时，钟差参数与硬件延迟参数无法分离。接收机硬件延迟对每颗卫星相同，与接收机钟差不可分离，卫星硬件延迟对每个接收机相同，与卫星钟差不可分离。IGS组织通常将接收机硬件延迟和卫星的硬件延迟分别并入接收机和卫星钟差参数中进行钟差解算[1-4]。即

(5)

则此时观测方程变为

(6)

(7)

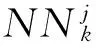
(8)

按式(4)和和式(5)解得的卫星钟差是以双频P码消电离层组合为基准的钟差，包含了P1和P2码观测量的卫星硬件延迟。但并不是所有的接收机都能够提供P1和P2观测量，因此在利用非P1/P2型接收机观测值进行卫星钟差求解时必须对P1和C1观测量的硬件延迟进行改正，以保证观测量与P1和P2观测值的完全一致性。

目前市场上的接收机主要分为三种，一种是P1/P2型接收机(如ASHTECHZ-Xll3T)，能够同时捕获C1、P1和P2观测值；一种是C1/P2型接收机(如LEICAGX1230)，能够通过特殊的跟踪技术同时捕获C1和P2码；另一种是C1/X2型新型接收机(如Trimble4000)，能够通过交叉相关技术提供C1码和一个特殊的码观测值线性组合X2码[1-5]。解算时，当数据中包含不同类型接收机接收到的数据时，应当考虑不同观测量的硬件延迟偏差，以保证其与P1和P2观测值的一致性。表1给出了不同类型接收机的硬件延迟改正方式，对于消电离层组合，P1/P2型接收机不需要对硬件延迟进行改正，C1/P2型和C1/X2型接收机，只需要对码消电离层组合观测值加一个特定的和P1和C1码观测量的硬件延迟BP1-C1相关的改正。

表1 不同类型接收机硬件延迟偏差的改正方法

IGS组织成立相应的工作小组负责每月发布一次GPS卫星不同码观测量间的硬件延迟偏差。图1画出了2012年1月的不同卫星的BP1-C1值。

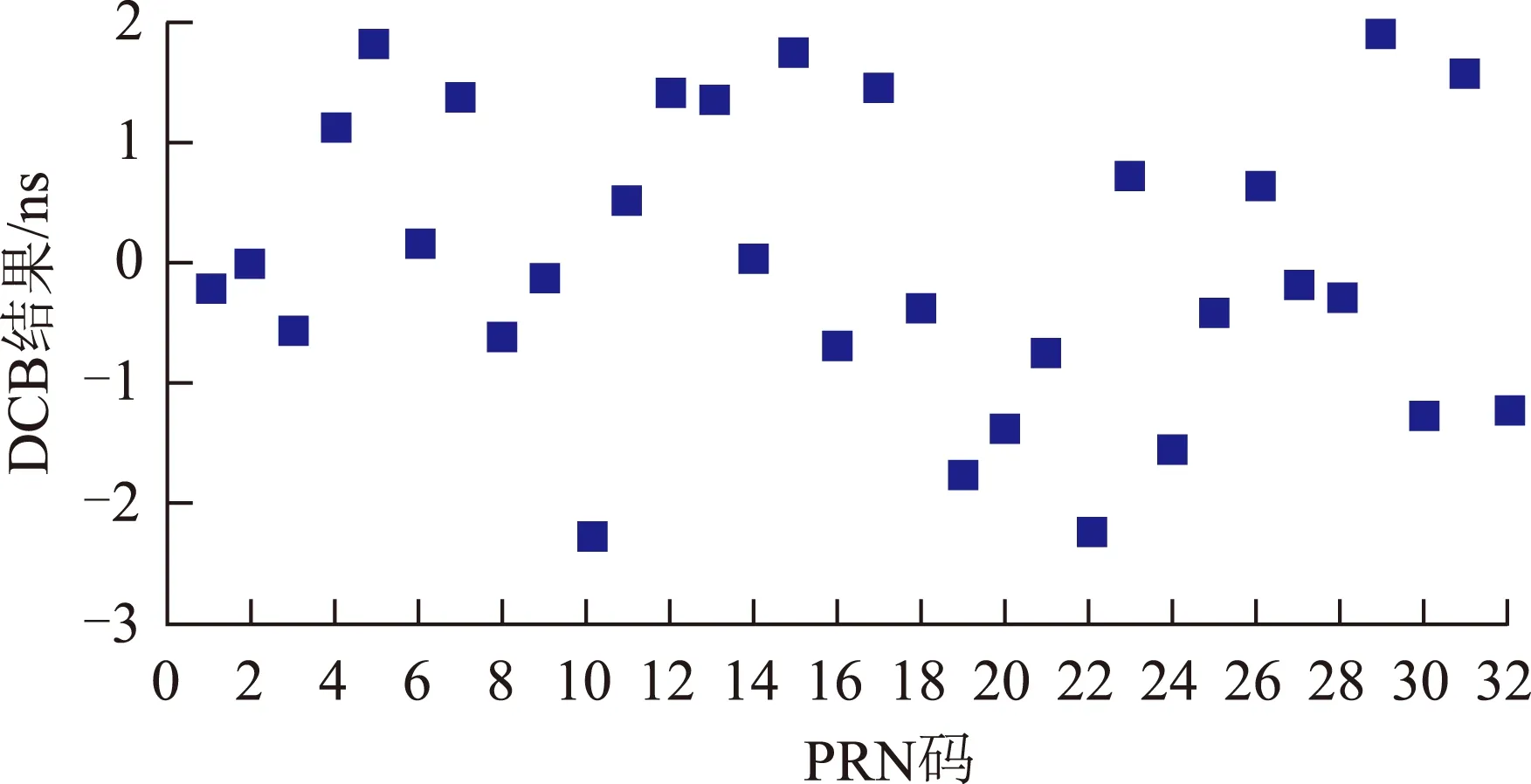
图1 2012年1月GPS卫星P1和C1码观测量的硬件延迟

3 DCB对卫星钟差解算的影响

为了考察DCB对卫星钟差解算的影响，收集了2008-05-27日ACOR、MADR、SCOA、SFER、TLSE五个IGS参考站组成的一个区域网络的数据，分别采用加DCB改正和不加DCB改正两种方法进行钟差解算实验，其中MADR和SCOA站接收机为P1/P2型接收机，ACOR、SFER站接收机为C1/P2型接收机、TLSE站接收机为C1/X2型新型接收机[6-7]。卫星钟差的精度评估一般采用二次差法[8-10]。本文以IGS提供的事后精密卫星钟差作为真值，选定一颗基准星，将计算结果与IGS事后精密钟差作二次差，分析DCB改正对卫星钟差解算的影响。

图2～图5分别表示以3号卫星为基准星得到的11、14、19、25四颗卫星的二次差时间序列。图6表示两种方法解算得到的11、14、19、25四颗卫星的钟差精度的统计结果。

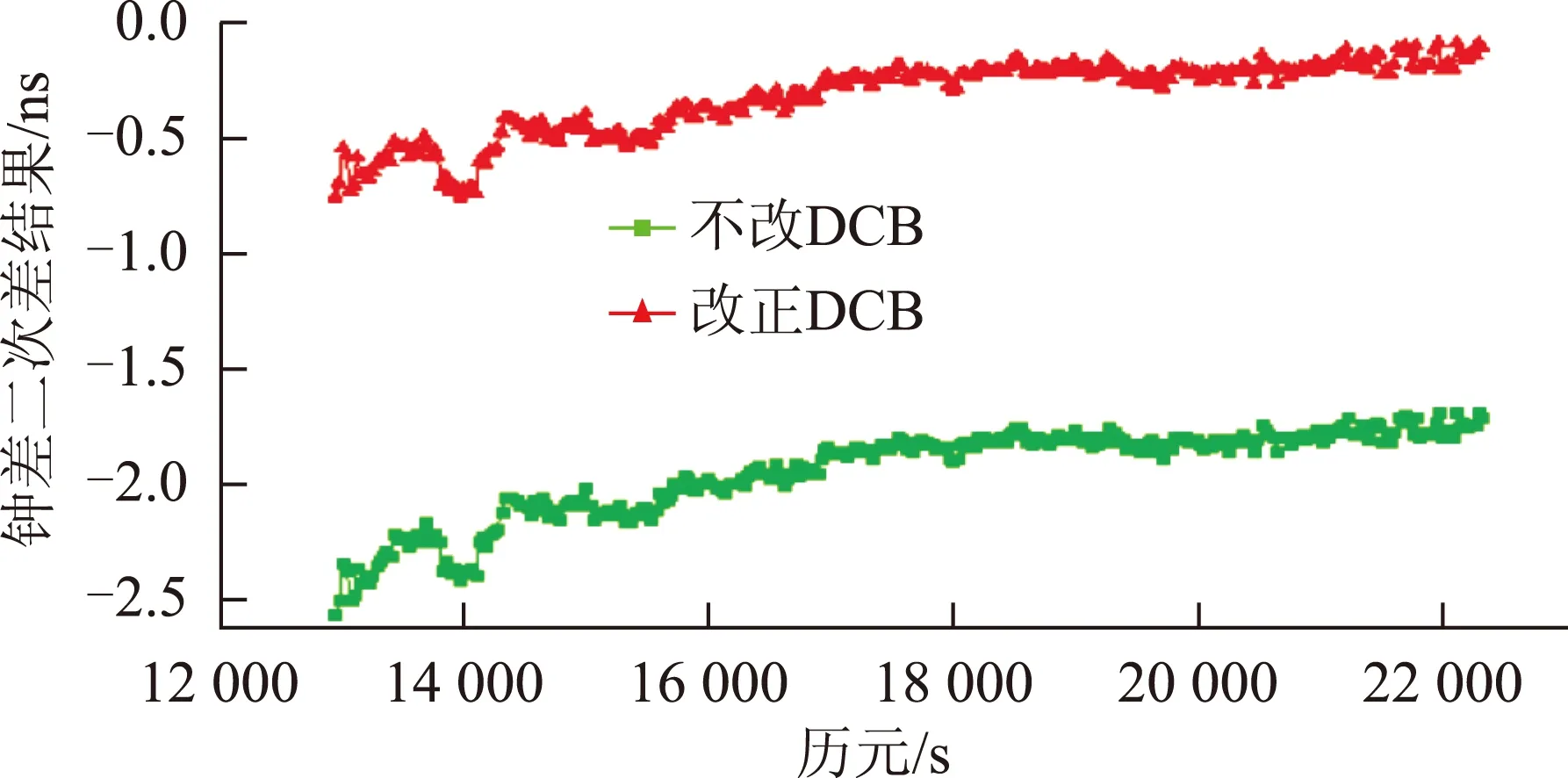
图2 11号卫星二次差时间序列

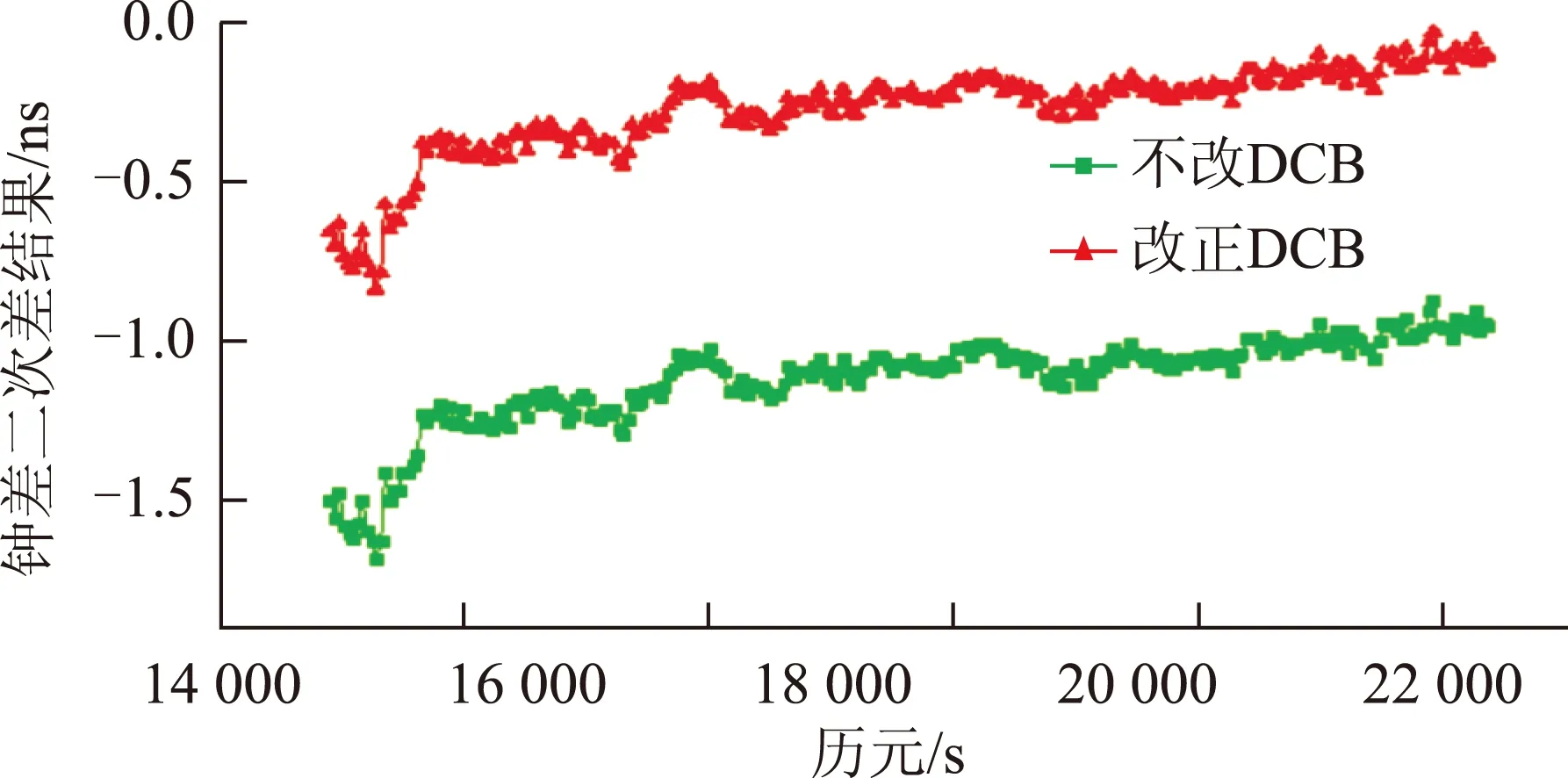
图3 14号卫星二次差时间序列

图4 19号卫星二次差时间序列

图5 25号卫星二次差时间序列

从图2～图5可以看出，两种方法解算得到卫星钟差二次差时间序列变化趋势基本一致，由图6知，同一卫星的钟差噪声水平(SD)也基本一致，通过计算得出两者相差不超过0.01 ns，但未加DCB改正的计算结果与加DCB改正的计算结果存在着系统性偏差一般为0～3 ns之间，这一系统性偏差与卫星有关，不同卫星的系统性偏差有所不同。考虑到系统偏差与卫星有关，这很可能是由于未改正硬件延迟偏差时，卫星的硬件延迟被部分吸收到对应卫星钟差中引起的。

图6 四颗卫星的钟差精度的统计结果

4 结束语

IGS公布的卫星钟差产品以双频P码消电离层组合为基准的钟差，已经包含了P1和P2码观测量的卫星硬件延迟。实验结果表明，改正DCB和不改正DCB两种方法解算得到卫星钟差二次差时间序列变化趋势基本一致，同一卫星的钟差噪声水平基本相等。

DCB对卫星钟差解算结果的影响表现为系统性的误差，这一系统性偏差与卫星有关，不同卫星的系统性偏差不同。其对卫星钟差的影响可以达到2 ns，因此在卫星钟差解算时应当对硬件延迟加以考虑。

致谢：感谢全球连续监测评估系统(IGMAS)信息工程大学分析中心对本文工作的支持和帮助。

[1] 宋伟伟.导航卫星实时精密钟差确定及实时精密单点定位理论方法研究[D].武汉：武汉大学，2011：29-61.

[2] 楼益栋.导航卫星实时精密定轨与钟差确定[D].武汉：武汉大学，2008：55-70.

[3] DACH R，HUGENTOBLER U，FRIDEZ P，et al.Bernese GPS Software Version 5.0[M].Bern：Astronomical Institute，University of Bern，2007：289-307.

[4] 黄健，汪平，阮仁贵，等.DCB对精密单点定位精度影响研究[J].大地测量与地球动力学，2010，30(3)：110-117.

[5] 阮仁桂.GPS非差相位精密单点定位研究[D].郑州：信息工程大学测绘学院，2009：15-16.

[6] SALAZAR D，HERNANDEZ-PAJARES M，JUAN J M，et al.GNSS Data Management and Processing with the GPSTK[J].GPS Solution，2010(14)：293-299.

[7] SALAZAR D.Precise GPS-based Position，Velocity and Acceleration Determination：Algorithms and Tools[D].Catalunya，Spain：Universitat Politecnica de Catalunya (UPC)，2010：74-80.

[8] 楼益栋，施闯，周小青，等.GPS精密卫星钟差估计与分析[J].武汉大学学报：信息科学版，2009，34(1)：88-91.

[9] 蔡华，赵齐乐，楼益栋.精密卫星钟差确定系统的实现与精度分析[J].武汉大学学报：信息科学版，2009，34(11)：1293-1296.

[10]李浩军，王解先，王虎，等.基于GNSS网络的卫星精密钟差估计及结果分析[J].武汉大学学报：信息科学版，2010，35(8)：1001-1003.

Impact of DCB on the Estimate of Satellite Clock Bias

YU He-li1，HAO Jin-ming1，XIE Jian-tao1，ZHOU Ying2，ZHENG Guo-qing3

(1.College of Navigation and Aerospace Engineering，Information Engineering University，Zhengzhou 450052，China； 2.Troops 61287，Kunming 650102，China；3.Troops 61206，Beijing 100042，China)

The hardware delay of different types of observation is different，the correct method of different code bias(DCB) when using ionosphere-free linear combination to estimate satellite clock bias was given，and quantitatively analyzed the influence of DCB on satellite clock estimate through experiments.Results show that DCB can caused a systematic bias that associated with satellite，this deviation could be 2 ns，so it must be dealt with carefully.

hardware delay；ionosphere-free linear combination；different code bias；satellite clocks；systematic bias

2014-04-25

于合理(1989)，男，河南周口人，博士，主要从事导航卫星精密钟差快速确定方法研究。

P228

A

2095-4999(2015)-01-0071-03