基于双频伪距组合评估北斗广播电离层精度

程 娜，贾小林

(1.长安大学 地质工程与测绘学院，西安 710054；2.西安测绘研究所，西安 710054)

基于双频伪距组合评估北斗广播电离层精度

程 娜1，贾小林2

(1.长安大学 地质工程与测绘学院，西安 710054；2.西安测绘研究所，西安 710054)

电离层时延误差是影响全球卫星导航系统定位、导航、授时精度的主要因素之一，为了满足单频用户的需求，我国北斗系统采用Klobuchar 8参数模型进行电离层时延改正。在监测评估体系中，采用两种方法对电离层预报精度进行评估，1)全球卫星导航系统国际服务协会精密电离层模型评估；2)双频伪距组合评估。基于第二种方法对北斗系统的Klobuchar模型进行了评估。评估结果显示，北斗系统广播电离层模型绝对精度包括均方根及标准差都在1.0 m以内；相对精度PER一般为50%左右。

电离层时延；北斗系统；Klobuchar模型；双频伪距组合

1 引言

北斗卫星导航系统简称北斗系统(BeiDou navigation satellite system，BDS)自2012年底已提供正式运行服务，目前在轨工作卫星14颗，包括5颗地球静止轨道(geostationary Earth orbit，GEO)、5倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)及4颗中圆地球轨道(medium earth orbit，MEO)[1-2]。对系统各项服务性能进行全面测试与评估，是系统提供服务的基础。空间信号性能评估是卫星导航系统服务性能评估的关键。其中，卫星信号在传播的过程中受电离层影响不可忽视，BDS采用基于地理系下的Klobuchar模型进行修正，以导航电文方式每2 h向用户发播一组电离层参数[3]。

电离层精度的评估采用两种方法，方法一是利用双频组合计算的电离层延迟量对预报的电离层精度进行评估，方法二是利用全球卫星导航系统国际服务协会(international global navigation satellite system service，IGS)或者欧洲欧洲定轨中心(center for orbit determination in Europe，CODE)电离层模型计算的电离层延迟量对预报电离层模型精度进行评估[4]。利用双频伪距进行组合可计算出电离层延迟改正量，同时通过导航电文发播的电离层模型参数(Klobuchar及其改正模型)，结合测站和卫星的位置，可计算出预报的电离层延迟改正量，由于双频组合计算的电离层改正量精度非常高，以其为参考即可对预报的电离层精度进行评估。

本文基于双频伪距组合评估BDS预报电离层精度，在M_DCB软件的基础上增加广播电离层延迟改正和双频伪距组合计算电离层延迟模块，对BDS电离层模型做出评估。

2 估计原理

2.1 BDS电离层模型

BDS采用与GPS相同的Klobuchar电离层模型进行电离层延迟改正，该模型通过描述电离层延迟周日变化的振幅、周期、初始相位以及它们的变化来描述电离层的周日变化，此外，BDS的Klobuchar模型采用的是日固地理坐标系，地理经度与时间具有较好的一致性，能更好的反映电离层的周日变化。BDS的Klobuchar模型8参数根据中国区域监测网的实测GNSS双频观测数据解算得到，2 h更新一组[3]。

用户利用8参数和Klobuchar模型可计算B1I信号的电离层垂直延迟改正Iz(t)， 单位为s，具体形式为[5-6]

(1)

式(1)中，t是以s为单位的接收机至卫星连线与电离层交点(M)处的地方时(取值范围为0～86 400)。对于计算不同频率的Iz(t)， 需要乘以一个与频率有关的因子k(f)； 电离层的参考高度为375km；A2为白天余弦曲线的幅度，用αn系数计算得到，即

(2)

A4为余弦曲线的周期，单位为s，用βn系数求得

(3)

通过上面式子可由8个参数计算出穿透点的垂直电离层延迟。

2.2 双频伪距组合评估

利用双频伪距观测量可组合计算出电离层延迟改正量，基本式为

(4)

式(4)中，f1,f2为对应的两个频率，Δρ为P1和P2码测得的伪距之差。

通过广播的模型参数已计算出了预报的电离层延迟，通过与事后双频组合计算出的电离层在垂直方向的投影量进行比对。即可对预报的电离层精度进行评估。由于发播的电离层参数计算的电离层改正量不包含卫星和接收机的频间偏差，因此需要对卫星和测站的频间偏差进行修正。计算频间偏差的观测方程为

(5)

式(5)中需要估计电离层参数和接收机、卫星的频间偏差。由于P4存在很大噪声，因此采用载波相位平滑伪距，平滑方法采用L4组合法平滑伪距[7]，在此不作详细介绍。

同时估计接收机、卫星频间偏差及电离层参数是首先需要选择合理的电离层数学模型。在计算时采用球谐函数电离层模型，观测方程可写为[8]：

(6)

3 精度分析

本文选用2013年004～007这 4d的数据，包括观测数据、电离层参数、CODE电离层产品，进行计算、比对。

3.1 建模精度

采用国内23个站(BJFS、CHUN、DLHA、GUAN、HLAR、HRBN、JIXN、KMIN、LHAS、LUZH、QION、SHAO、TAIN、TASH、TWTF、URUM、WUHN、WUSH、XIAA、XIAG、XNIN、YANC、ZHNZ)建模，如图1所示。

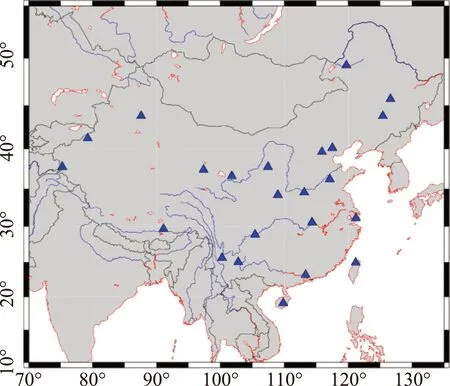
图1 测站分布图

3.1.1 内符合精度

利用观测资料建立该时段的区域性电离层模型，并根据拟合后的残差来计算模型的内符合精度[9]。

(7)

验后单位权中误差，作为电离层建模的内符合精度。

3.1.2 外符合精度

模型计算VTEC值与CODE GIM内插值做差，统计建模的外符合精度，统计公式如下[10-11]：

(8)

(9)

建模精度统计结果见表1。

表1 建模精度统计

图2显示：卫星DCB估值与CODE DCB差值一般在±0.5 ns以内，个别卫星超过1.0 ns，如PRN27号卫星偏差较大，可能由于国内站观测数据中G27卫星观测数据不足。RMS都在0.4 ns以内。

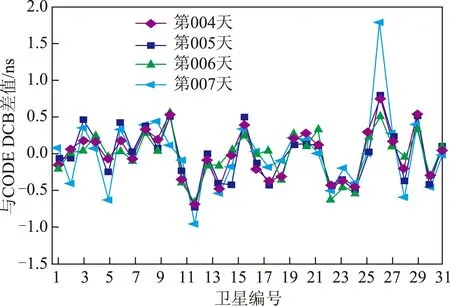
图2 卫星DCB精度

3.2 电离层模型精度

目前常用的评价广播电离层时延修正模型精度的指标分为绝对精度和相对精度两种。其中，平均值(Mean)、标准差(standard deviation，STD)与均方根均方根(root mean square，RMS)为绝对精度指标，分别表示基于广播电离层时延修正模型计算的电离层延迟与基准电离层延迟之差的Mean、STD及RMS；PER表示广播电离层时延修正模型相对于基准电离层延迟的修正百分比，为相对精度指标，具体形式为[6]：

(10)

(11)

式(10)及式(11)中，PERn表示第n个观测历元的修正百分比；DRmodel,n,DRref,n分别表示广播电离层模型和双频组合计算得到的第n个观测历元电离层延迟改正的平均值；N为统计期间观测历元个数；

本文采用2013年1月数据来评估BDS预报电离层模型精度。其中统计了BJFS站4 d的模型修正结果和双频伪距组合电离层延迟改正量，结果如图3所示：图3中，DION1为模型改正量，dion为双频组合计算的延迟改正量。

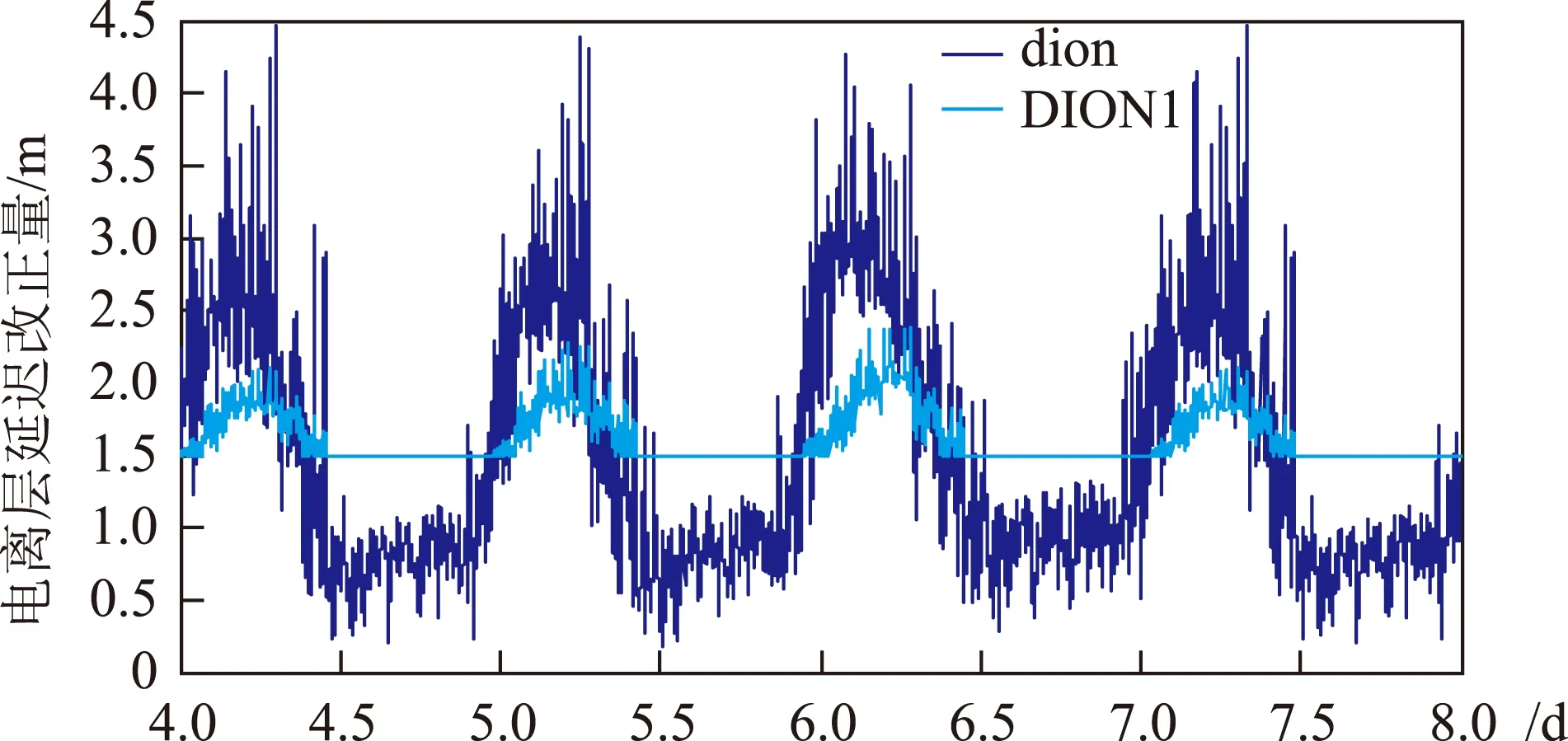
图3 电离层时延改正

表2 BJFS站电离层时延改正模型精度指标统计

年积日/dMean/mRMS/mSTD/mPER0040.110.630.6253.6%0050.140.640.6355.0%006-0.080.660.6563.2%007-0.211.041.0245.8%

从表2可以看出，BDS的Klobuchar电离层时延改正模型绝对精度RMS、STD在1.0 m以内，相对精度则较低，一般在50%左右。此外，最大垂直总电子含量为30 TECu，处于电离层活动低年。

4 结束语

中国区域低阶球谐函数建模精度为1.0～2.0TECU，卫星DCB相对CODE产品偏差一般在0.5 ns左右，RMS在0.4 ns以内；接收机DCB具有较好的稳定性。双频伪距组合评估BDS广播电离层延迟改正，绝对精度小于1.0 m，相对精度一般在50%左右。

[1] 陈良，焦文海，黄晓瑞，等.北斗卫星导航系统空间信号精度计算方法与评估研究[C]//第四届中国卫星导航学术年会论文集.武汉：中国卫星导航学术年会，2013.

[2] 杨元喜，李金龙，王爱兵，等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学：地球科学，2014，44(1)：76-85.

[3] WU Xiao-li，HU Xiao-gong，WANG Gang，et al.Evaluation of COMPASS Ionospheric Model in GNSS Positioning[J].Advances in Space Research，2013，51(6)：959-968.

[4] 高为广，苏牡丹，郭树人，等.北斗系统空间信号精度测试与评估[C]//第四届中国卫星导航学术年会论文集.武汉：中国卫星导航学术年会，2013.

[5] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件(1.0版)[R/OL].(2012-12-01)[214-05-26].http：//www.beidou.gov.cn/attach/2012/12/27/2012122755318f7eabbe451aa6d052f829f92e50.pdf.

[6] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2005.

[7] 蔡昌盛，李征航，赵晓峰.利用GPS组合观测值建立区域电离层模型研究[J].测绘工程.2003，12(1)：15-18.

[8] JIN Rui，JIN Shuang-gen，FENG Gui-ping.M_DCB：Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases[J].GPS Solution，2012，16(4)：541-548

[9] 刘长建.GNSS电离层建模方法与质量控制研究[D].郑州：解放军信息工程大学，2011.

[10]章红平.基于地基GPS的中国区域电离层监测与延迟改正研究[D].上海：中国科学院上海天文台，2006.

[11]李子申.GNSS/Compass 电离层时延修正及TEC监测理论与方法研究[D].武汉：中国科学院测量与地球物理研究所，2012.

Precision Assessment of Broadcast Ionospheric Model of BDS Based on Double-frequency Pseudo-range Combination

CHENG Na1，JIA Xiao-lin2

(1.School of Geology Engineering and Surveying，Chang’an University，Xi’an 710054，China；2.Xian Research Institute of Surveying and Mapping，Xi’an 710054，China)

Ionospheric delay is one major factor which affecting GNSS positioning，navigation，timing (PNT).In order to meet the needs of single-frequency users，the BDS provides the Klobuchar 8-parameters correction model in geographic coordinate system for ionospheric delay.In the monitoring and evaluation system，there are usually two methods to assess the broadcast Ionospheric model，1) assessment by IGS precise ionospheric；2) assessment by dual-frequency pseudo-orange combination.In this paper，the second method is used to assess the BDS’s broadcast ionosphericmodel.The results show that RMS and STD of broadcast ionospheric model are in 1.0 m，the relative precision is usually about 50%.

ionospheric delay；BDS；Klobuchar model；double-frequency pseudo-range combination

2014-05-19

程娜(1991)，女，山东巨野人，硕士生，主要从事卫星导航与定位研究。

P228

A

2095-4999(2015)-01-0074-04