一道错题引发的教学思考

洪菲菲

教学“2、3、5的倍数的特征”这一内容时，学生作业中的一道错题令笔者颇为不解。这是一道判断题：个位上是3、6、9的数是3的倍数。其实，随意举个例子都可以驳斥这句话，轻而易举就能得出正确判断。但奇怪的是，有不少学生都认为这句话对。学生们常以为“51、57、87”是质数，这也与学生对3的倍数特征不敏感有关。

一、深入开掘，剖析错因

为什么看似简单的学习内容，学生却难以接受，屡犯“低级错误”呢？

1.受“2和5的倍数特征”的负迁移

相比2、5的倍数的特征而言，3的倍数的特征不那么直观明显且易于理解。孩子们从认识1、2、3……开始，就已经自觉不自觉地2个2个数数，5个5个数数，积累了非常丰富的2、5的倍数的经验，所以在学习2和5的倍数特征时，可谓轻而易举，手到擒来。这些从小积累的数数经验，虽为学生学习2、5的倍数特征提供了坚实的基础，但也对3的倍数特征的教学带来了强烈的干扰，产生了巨大的负迁移作用。学生们习惯了在个位上找寻倍数特征，误认为3的倍数特征也在个位上就情有可原了。

2.“浮于表面”的浅探究所致

要“对抗”学生固有的“个位情节”，需要教师在教学中引导学生深入探究。在教学“3的倍数特征”时，学生们虽也经历了“猜测—验证—推翻猜想—再观察—再猜测—再验证—得出结论”的探究过程，但多数是浮于表面的浅探究。

（1）自己找，还是教师给？

学生在初次猜测3的倍数特征时，往往提出“个位上是3、6、9的数是3的倍数”，这时让学生列举几个数便可轻易推翻这条结论。然而，失去了唯一的可寻线索，学生往往陷入茫然。即便写出了一些3的倍数，也难以从中找到新的思路。这时，大多数教师会适时提出——“把3的倍数的各位上的数相加，看看有什么发现？”虽然教师的点拨为学生指出了一条“康庄大道”，但教师的“给予”能给学生留下多深的印象？这种教师指引下的“动作”是“自主探究”吗？失去了“发现问题、提出问题”的过程，也就失去了探究的意义，无怪乎学生对“3的倍数特征”不敏感，这与教师的“给予”不无关系。

（2）知其然，还要知其所以然

在教师的指引下，学生计算了“12、15、18、21、24、27……”等数各位上的数的和，很快发现了3的倍数的特征。在总结出特征之后，教师往往让学生进一步验证，自己列举一些数，看这条特征是否“放之四海皆准”。充分验证之后，再引导学生总结出3的倍数特征，教学至此完成。只是，学生在总结出特征之后，心里是否会产生疑问——“为什么要将各位上的数相加呢？” 没有解开这个心结，学生的掌握仅止在“操作层面”。缺少了对其中道理的理解，就如同“无源之水、无本之木”，犯错误也就在所难免。

二、对“症”开方，由表及“理”

“2、5倍数的特征”的负面干扰不可避免，教师通过引导学生进行有效探究，则完全可以帮助学生真正掌握好这一内容。

1.在有序排列中寻找规律

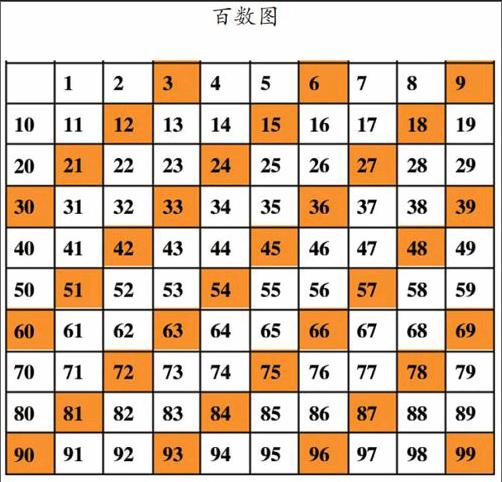
在2、5倍数特征的教学中，学生只要随意写出几个2或5的倍数，即可很快发现其倍数特征。而3的倍数特征较为“隐蔽”，学生写出一些3的倍数后，仍难以发现其中的规律。然而，规律只有经由“独立发现探索”才能真正进入学生们的心里。因此，教师可以利用百数图，使3的倍数呈有序排列，以便学生在观察的时候自主发现规律。教师不妨开展如下教学活动。

师：同学们，这是一张百数图，请你们将3的倍数涂上颜色。（学生活动）

师：请你们观察一下，这些3的倍数有没有什么特征？你能找到什么规律吗？

生：这些数都是斜着整齐排列的。

生：每一斜行上的数有规律，头尾的数字调换过来了。比如右下角最后一斜行，69和96，78和87。其他斜行也有这样的规律。

生：每个斜行上的数两个数位上的数相加的和是一样的。第一个斜行的数两个数位上的数字相加等于3，第二斜行等于6，其他的分别等于9、12、15……

生：我发现这些数两个数位上的数的和有规律，都是3的倍数。

师：你们能大胆猜想一下，3的倍数有什么特征吗？

生：把一个数每个数位上的数字相加，如果是3的倍数的话，这个数就是3的倍数。

师：这是你的猜想，有了猜想，我们还要……对，验证。现在，请你们任意写出一些数，先根据你们的猜想判断一下是不是3的倍数，再实际算一算。

学生举例验证，全班交流……

在上述教学片段中，教师充分利用了百数图这一学习工具，使3的倍数呈现有序排列，便于学生观察，并自主发现规律、提出猜想。学生经这番“观察—发现—猜想”的过程，将获得更加深刻的切身体会，丰富其数学活动经验，从而促进对3的倍数特征的理解。这比教师“直接提示”效果要好得多。

2.在深入剖析中理解规律

学生经历了“提出猜想—举例验证—得出结论”之后，对3的倍数特征有了较为深刻的认识。然而，过了一段时间之后，学生对3的倍数特征遗忘得较多。究其原因，在于学生对3的倍数特征的认识仅止于“面”上，即学生仅从数的表面了解了3的倍数特征，而对于“为什么要将各个数位上的数字相加”则 一无所知，无怪乎学生容易遗忘。虽然教材中并未要求学生理解3的倍数特征其中的道理，但如果将其中算理稍作介绍，可以使学生的认识由表及“理”，更加深刻透彻，也就能避免一些错误的发生。

师：通过刚才的验证，我们知道了3的倍数有什么特征？

生：把一个数各个数位上的数字相加，如果结果是3的倍数，这个数就是3的倍数。

师：关于3的倍数特征，你还有什么想了解的吗？

生：我想知道，为什么要将各个数位上的数字相加来判断是否是3的倍数，而不是看个位上的数呢？

师：这个问题很有价值，你们想过其中的道理吗？141是不是3的倍数？

生：是。

师：我们来看看为什么可以用（1+4+1）的和来判断141是否是3的倍数，你们瞧。

课件演示：

师：看明白了吗？谁来说说为什么可以用（1+4+1）的和来判断141是否是3 的倍数，这三个数字分别表示什么意思？

生：百位上是1个百，3个3个的分，还剩1;十位上是4个十，3个3个的分，还剩4;个位上是1，不能3个3个分，还剩1。三个数位上一共剩下（1+4+1=6）个小正方形，6还可以分成2个3，所以141是3的倍数。

师：以此类推，你们能不能再举一个例子来说明一下。

在上述教学片段中，教师利用方格图直观演示，使学生清晰地看到将一个数各个数位上的数字相加来判断是否是3的倍数的道理所在。对算理的进一步探究，捅破了学生认知中的最后一层“窗户纸”，使之达到了“法”“理”相融、深入掌握的程度。

通过对一道错题的深入分析，笔者发现，学生掌握一个数学知识点不能仅依靠教师口耳相授，也不能单纯依赖机械模仿。学生只有自己发现、感悟、操作，才能丰富学习体验，学好每一部分知识。且在掌握方法的同时，应该理解其中的道理所在，明晰了“理”，才能达到对知识的真正掌握。