本原BCH码参数的盲识别方法
王兰勋,熊政达,孙旭丽
(河北大学 电子信息工程学院,河北 保定 071002)
本原BCH码参数的盲识别方法
王兰勋,熊政达,孙旭丽
(河北大学 电子信息工程学院,河北 保定 071002)
针对本原BCH码编码参数的盲识别,首先,根据循环移位前后码字的最大公约式的阶数,利用实际序列与随机序列阶数概率分布差异最大的特性,提出一种基于变异系数识别码长的方法。在此基础上,根据码字之间的线性约束关系,以阶数概率最大值为下限,通过计算概率总和来识别起始点,进而,计算邻域半径快速去除含错码字,根据阶数分布最大值识别生成多项式,实现了BCH码的盲识别。理论分析及仿真实验表明,该算法简单易行,在误码率为0.01的条件下识别效果较好,容错性较强。
BCH码;盲识别;阶数概率分布;生成多项式
在数字通信系统中,为抗击传输中噪声的干扰,通常在信息序列中增加冗余码元,以提高数据传输的可靠性。而对于信息截获方,为获取更多信息,需要对截获数据的编码体制和参数进行识别。因此,信道编码技术[1]和信道编码盲识别技术[2]在通信工程领域具有重要的应用价值[3]。
目前,据现在公开发表的文献可知,大部分主要集中在卷积码的盲识别上,较少研究循环码。文献[4]根据比特率检测法识别码长和起始点,文献[5]根据码重分布概率方差识别码长,计算码多项式的公约式求解生成矩阵,二者均对低码率的分组码识别效果较好;文献[6]根据矩阵秩信息熵识别码长及码重信息熵识别起始点,但需多次构造矩阵,文献[7]根据对偶码字的统计特性,并判断对偶空间归一化维数的最大值识别码长和起始点,但迭代次数较多,二者均运算时间较长且计算量较大;文献[8]根据欧几里德算法得到最大公因式,完成对码长及生成多项式的识别,文献[9]根据概率逼近的算法,利用概率门限,在不同的域间搜索并识别码长,利用根的连续性及共轭根系的性质,识别生成多项式,二者容错性较好,但起始点已知;文献[10]根据最大公约式指数的相关性估计码长,并利用傅里叶变换实现生成多项式的识别,虽无复杂计算,但GFFT是有限域上的矩阵运算,随码长和数据量的增加,运算量会急剧增加。
上述的识别算法,计算量大、容错性一般或起始点已知,针对这些不足,本文根据最大公约式阶数概率分布的差异对BCH码编码参数进行识别,理论分析并与其他算法进行比较,仿真结果表明,本算法复杂度低,计算量小,在高误码率为0.01时能够识别码长和起始点,且效果明显。
1 BCH码的定义及分析
定义1[11]:给定任一有限域GF(q)及其扩域GF(qm),其中q是素数或素数的幂,m为某一正整数。若码元取自GF(q) 上的一循环码,它的生成多项式g(x)的根集合R中含有以下δ-1个连续根时,则由g(x)生成的循环码称为q进制BCH码。
R⊇{am0,am0+1,…,am0+δ-2}
(1)
当q=2且n=2m-1时,称这类码为二进制本原BCH码。
定义2[11]:若(f(x),g(x),…,k(x))是同时除尽多项式f(x),g(x),…,k(x)的次数最高的首一多项式,则称(f(x),g(x),…,k(x))是f(x),g(x),…k(x)的最大公约式。
定义3[11]:BCH码是纠正多个随机错误的循环码,且码字多项式c(x)应当满足如下等式
c(x)=m(x)g(x)
(2)
式中:g(x)称为生成多项式,可表示为:g(x)=xn-k+gn-k-1·xn-k-1+…+g1x+g0,即c(x)是g(x)的倍式,因此,g(x)是BCH码中次数最低的多项式。
辗转相除法[12]:求二元域上两个多项式的最大公约式,其所有计算均为模二和运算,具体步骤如下:
1)任取一接收的码字为C,将其作为被除式写在第一行,并将码字C循环移动m位后得到新的码字为C1,将其作为除式写在第二行,两行均左端对齐且首位若为0,可省去不写。
2)被除式与除式进行相加,得到余式序列。
3)余式序列作为被除式,上一步中被除式作为除式,按照上述原则,进行相加,再次得余式序列。
4)反复进行第3步,直到余式序列全为0,则此时的被除式序列即为所求的最大公约式。
2 BCH码的参数估计
2.1 码长的识别方法
由上述定义可知,BCH码的码字与其m次循环移位后得到的码字必定含有一个最大公约式,当码长选取不正确时,码字类似为随机序列,则根据实际序列与随机序列最大公约式阶数概率分布间的差异,利用变异系数识别码长。
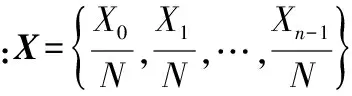
变异系数,简称CV,反映了相对波动的大小,通过变异系数的差值更能准确衡量出两个向量的差异程度,当变异系数差值越大,实际序列与随机序列相对波动越明显,当最大时,此时的码长即为真实码长,计算过程如下
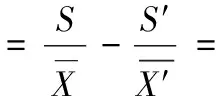
(3)
假设接收序列长度为R,码长的识别步骤如下:
1)初始化估计的有限域指数为m,范围为3≤m≤8,即从m=3依次进行遍历,则码长为n=2m-1。

4)根据式(3)计算ΔCV的值。
5)m=m+1,转到步骤1),计算不同域值m对应的变异系数的差值ΔCV。
6)计算完成后,找出ΔCV最大值,即域值m对应的码长估计值n即为真实码长。
2.2 起始点的识别方法
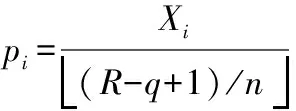
(4)
起始点的识别步骤如下:

2)同上述码长识别步骤3)计算方法相同,得到测试序列阶数的概率分布后,找到概率最大值并以此为下限,逐次相加,直到次数为n-1时的概率,利用式(4)计算概率和的值;
3)q=q+1,转到步骤1)继续执行,直到q=n+1,比较上述计算的结果,找出概率和的最大值,为准确地看出q值的位置,编程时保留最大值,令其他值为0,则该值对应的位置即为码字起始点。
2.3 生成矩阵的识别方法
在识别出码长和起始点的基础上,为达到无误码字最大化,提高码字的识别效率,应快速剔除含错码字。取1 000组码字得到(15,5)BCH码在不同误码率下最大公约式阶数的概率分布曲线图,如图1所示。

图1 不同误码率下阶数概率分布曲线图

(5)
3 仿真验证与结果分析
3.1 码长识别验证
为了验证识别方法的正确性和适用性,选取误码率Pe=0.02的(15,5)和Pe=0.01的(63,16)两种低码率BCH码以及Pe=0.02的(31,26)和Pe=0.01的(127,106)两种高码率BCH码,码组个数为103,运用MATLAB进行试验仿真,结果如图2 所示。
由图2可知,根据码组内具有完整的线性约束关系,码字循环移位后,实际序列与随机序列最大公约式阶数分布的概率相差较大,所以,遍历有限域值m对应的值ΔCV取最大时,此时m值对应的码长即为真实码长n。相反,当不是真实值时,实际序列的最大公约式阶数概率分布接近于随机序列,所以,ΔCV变化相对平稳。经仿真分析可知,该方法在一定的误码率条件下,不仅适用于低码率的码字,而且对高码率的码字也同样适用,且识别效果明显,容错性较好。

图2 码长识别仿真图
3.2 起始点识别验证
为验证起始点识别方法的正确性,选取误码率在Pe=0.06下(15,11)和Pe=0.02下(31,26)两种高码率的BCH码以及Pe=0.005下(127,50)低码率的BCH码,码组个数为103,运用MATLAB进行试验仿真,结果如图3所示。
由图3可知,在识别出码长的基础上,根据码字之间线性约束关系较强的特性,对3种不同码率的码字在一定的误码率下进行起始点识别。由图可知,依次对起始点进行遍历,统计最大公约式阶数的概率和,最大值分别出现在6、8、12,则该点即为起始点。可见,该方法对不同码长且码率不同的码字进行识别,容错性较好,识别效果较明显。
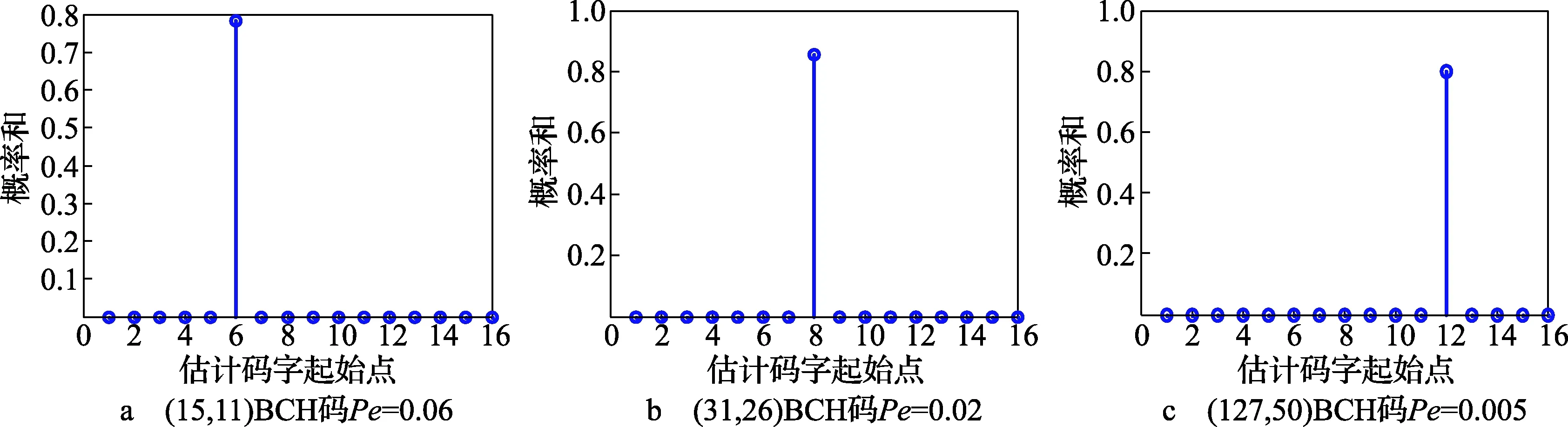
图3 码字起始点识别仿真图
4 生成矩阵求解及验证

图4 (15,5)BCH码阶数分布仿真图
经图4可知,当最大公约式次数为第10阶时,出现次数最多,根据定义3可知,g(x)是BCH码中次数最低的多项式,因此,选取该阶数对应的码字(循环移位前的接收码字),全零码进行剔除,找出码字中出现次数最低的多项式,该多项式即为生成多项式。截取部分多项式的仿真结果如图5所示,由图可以看出,次数最小的多项式即为生成多项式:g(x)=x10+x8+x5+x4+x2+x+1,即可完成识别。可见,该算法相对于文献[8],利用邻域半径δ,提高了正确码字的利用率,使其所需的数据量大大减小,计算量减小。

图5 (15,5)BCH码部分多项式仿真图(截图)
5 性能分析
5.1 算法复杂度分析比较
文献[13]基于码根信息差熵和码根统计来识别BCH码,在识别出码长的条件下,需遍历本原多项式,且码长越长,其本原多项式的个数越多,算法的复杂度也就越高,其复杂度为O(n3);文献[14]对m行n列的矩阵进行对角化,需进行m(m-1)/2 行和n(n-1)/2次列模二运算;文献[15]相对于文献[14]而言,可减少一半的计算量,只需进行n(n-1)/2次列模二运算,该算法的复杂度为O(n2);文献[16]基于稀疏沃尔什谱并利用Walsh-Hadamard变换进行识别,对于码长为n,信息位为k的BCH码,计算量主要为n(n-k)/2,则该算法的复杂度主要为O(n2);而本文基于辗转相除法,主要的复杂度仅为O(n),可见,该算法的计算复杂度优于上述文献。
5.2 算法容错性分析比较
在误码率取值不同的条件下,选取103组不同参数的码字进行500次蒙特卡洛仿真实验,得出码长和起始点识别率,如图6~图7所示。在误码率为0.02时,码长n≤31的码字识别效果高达90%;在误码率为0.006时,码长31≤n≤127的码字识别效果高达90%;而在起始点的识别上,在误码率为0.1时,(15,11)识别效果略高于(7,4)码。可得,随着码长与码率的增加,码字之间的线性约束关系降低,导致识别概率逐渐减小;同时,该算法在码长和码率不同的条件下,能有效识别码长和起始点,容错性较好。
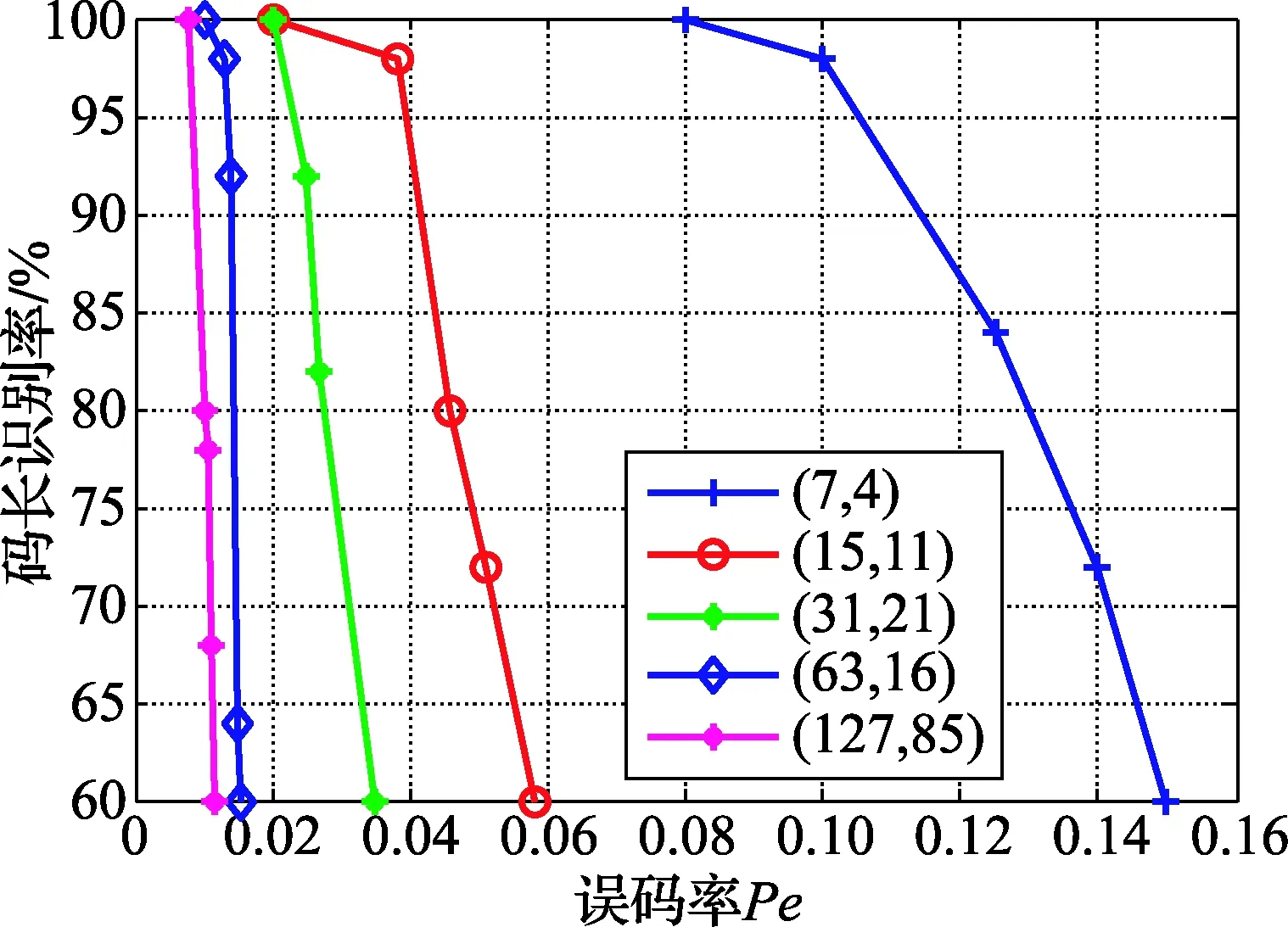
图6 码长识别概率曲线图
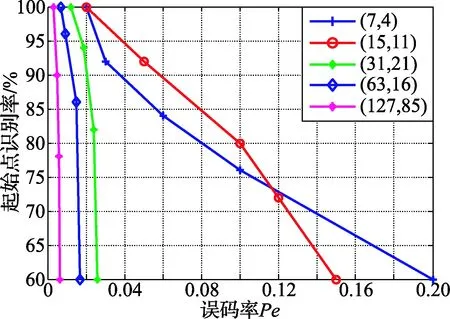
图7 起始点识别概率曲线图
BCH码也是一种线性分组码,选取数目种类相同的码字,对文献[5-6,15]和本文提出的码长识别算法进行比较,图8为不同算法的90%识别码长误码率上限[17]曲线图,以码长7为例,本文的误码率为12%,文献[5]的误码率为9%,文献[15]的误码率为5%,文献[6]的误码率为3%,仿真结果表明,在码长取值相同的条件下,本文识别算法抗误码的能力较强,容错性较好;同样,选取上述同样的码字,对文献[6,15]和本文提出的起始点识别算法进行比较,由图9可以看出,除码长为7的码字外,本文算法的抗误码能力优于文献[6,15]。
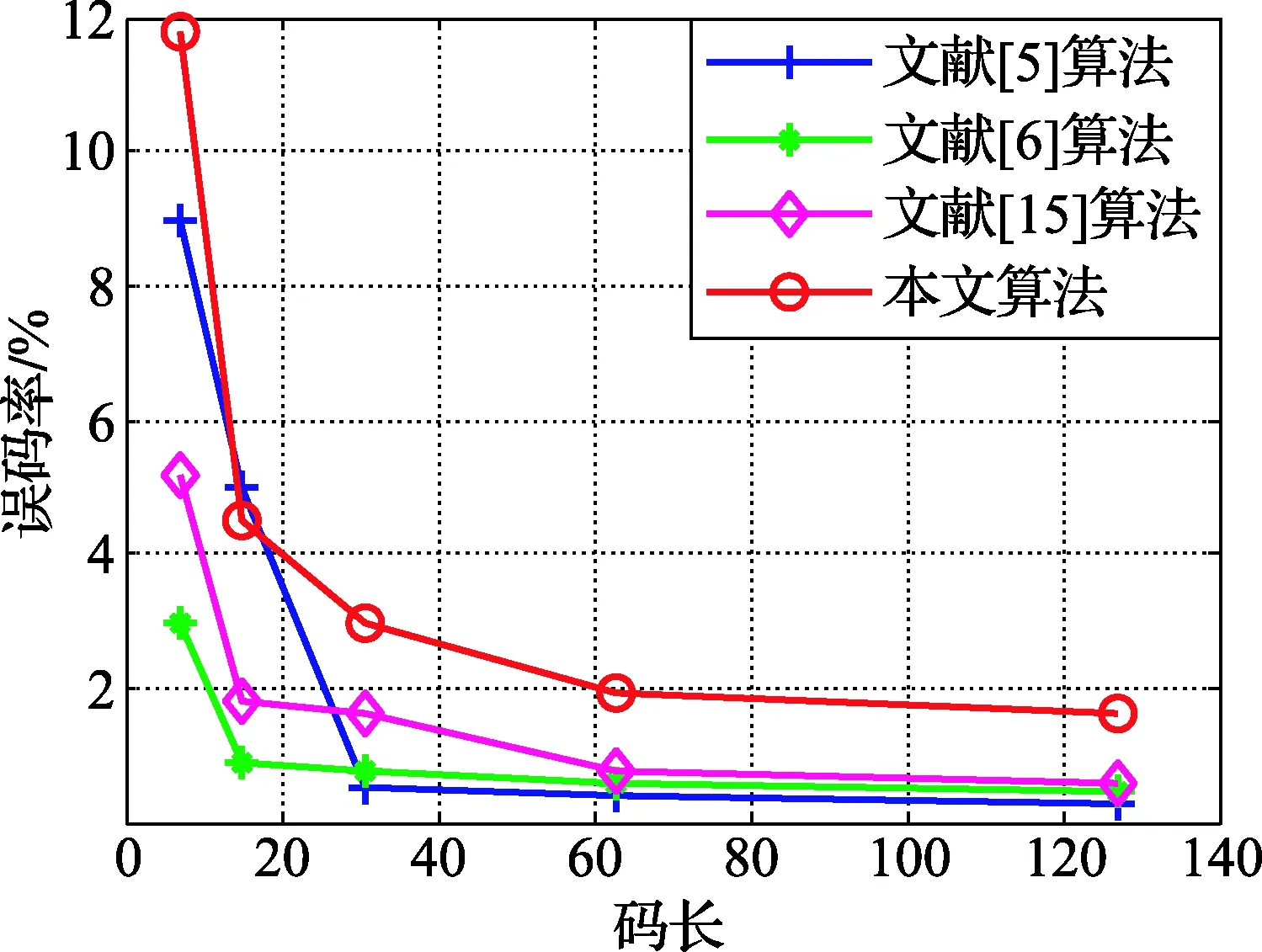
图8 不同算法的90%识别码长误码率上限
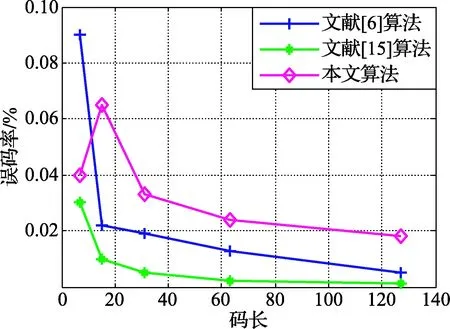
图9 不同算法的90%识别起始点误码率上限
6 结论
本文依据码字之间的线性约束关系及实际序列与随机序列最大公约式阶数概率分布的差异性,利用变异系数的差值识别码长并由概率和准确识别出起始点,在此基础上,通过设置邻域半径剔除含错码字,利用阶数分布最大值完成对生成多项式的识别,进而实现了BCH码参数的盲识别。最后,在不同的误码率下,对不同码率的码字进行了大量的仿真实验,并与其他算法进行比较,结果表明,该算法复杂度低,不仅针对低码率的码字,还可以对高码率的码字进行识别,且在误码率为0.01时识别效果较明显,容错性能较好。
[1] 解辉,黄知涛,王丰华.信道编码盲识别技术研究进展[J].电子学报,2013,41(6):1166-1176.
[2] 闫郁翰.信道编码盲识别技术研究[D].西安:西安电子科技大学,2012.
[3] 张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010.
[4] 陈金杰,杨俊安.一种对线性分组码编码参数的盲识别方法[J].电路与系统学报,2013,18(2):248-254.
[5] 邓瑞瑞,汪立新.基于码重分布概率方差的循环码识别方法[J].太赫兹科学与电子信息学报,2013,11(5):792-796.
[6] 陈金杰,计时钟,杨俊安.高误码条件下线性分组码的盲识别[J].应用科学学报,2013,31(5):459-467.
[7] 杨晓炜,甘露.基于Walsh-Hadamard变换的线性分组码参数盲估计算法[J].电子与信息学报,2012,34(7):1643-1646.
[8] 王兰勋,李丹芳,汪洋.二进制本原BCH码的参数盲识别[J].河北大学学报,2012,32(4):416-420.
[9] 阔永红,曾伟涛,陈健.基于概率逼近的本原BCH码编码参数的盲识别方法[J].电子与信息学报,2014,36(2):332-339.
[10] 戚林,郝士琦,王磊,等.一种RS码快速盲识别方法[J].电路与系统学报,2011,16(2):71-76.
[11] 王新梅,肖国镇.纠错码——原理与方法[M].修订版.西安:西安电子科技大学出版社,2001.
[12] 杜宇峰,裴昌幸.信道编码分析识别技术研究[D].西安:西安电子科技大学,2012.
[13] 杨晓静,闻年成.基于码根信息差熵和码根统计的BCH码识别方法[J].探测与控制学报,2010,32(3):69-73.
[14] 张永光,楼才义,王挺.一种线性分组码编码参数的盲识别方法:中国,201010131103.3[P].2010-10-13.
[15] 朱联祥,李荔.改进的二进制循环码盲识别方法[J].计算机应用,2013,33(10):2762-2764.
[16] 解辉,宋阳,王丰华,等.基于稀疏沃尔什谱的BCH码检测识别方法[J].中国电子科学研究院学报,2013,8(2):156-160.
[17] 王平,曾伟涛,陈健,等.一种利用本原元的快速RS码盲识别算法[J].西安电子科技大学学报,2013,40(1):105-110.
王兰勋(1956— ),教授,主要从事数字通信与信息编码方面研究;
熊政达(1989— ),女,硕士生,主研信道编码盲识别;
孙旭丽(1990— ),女,硕士生,主研信道编码识别的硬件实现。
责任编辑:时 雯
Blind Recognition Method of Primitive BCH Codes Parameters
WANG Lanxun,XIONG Zhengda,SUN Xuli
(CollegeofElectronicandInformationalEngineering,HebeiUniversity,HebeiBaoding071002,China)
In order to solve the problem of the blind recognition of primitive BCH code parameters, the code length are identified by the recognition method based on the coefficient of variation that is proposed by the most notable differences whose order of the largest common divisor probability distribution between the actual sequence and random sequence,by computing the order between the code word and its circular shift code word.On this basis, according to the linear constraint relationship between the code word,the starting point are identified by calculating the sum of all probability with the lower limit of maximum probability.The generator matrix is solved through the method of calculating the radius of neighbourhood to remove wrong words quickly and then getting the maximum of the order distribution,the blind recognition of primitive BCH codes is finally realized.The recognition method is simple,theoretical analysis and simulation results show that the method has better error-tolerance and the recognition has better performance in 0.01BER.
primitive BCH code;blind recognition; the greatest common divisor; generator matrix
河北省自然科学基金项目(F2014201168)
TN911.22
A
10.16280/j.videoe.2015.17.010
2015-07-10
【本文献信息】王兰勋,熊政达,孙旭丽.本原BCH码参数的盲识别方法[J].电视技术,2015,39(17).

