深基坑在土钉墙和桩锚联合支护条件下支护结构受力分析

程 岩 黄志全 高 稳

(1.中国建筑科学研究院 科技处，北京 100013； 2.华北水利水电大学，郑州 450045)

深基坑在土钉墙和桩锚联合支护条件下支护结构受力分析

程 岩1黄志全2高 稳1

(1.中国建筑科学研究院 科技处，北京 100013； 2.华北水利水电大学，郑州 450045)

本文通过数值计算得出土钉和锚杆所受内力呈“枣核”状或抛物线状分布，每排土钉轴力最大值自上往下逐渐向面层方向偏移。随着开挖深度的增加，受拉土钉的轴向拉力增大，而对于锚杆开始在自由段施加预应力，随着开挖深度的增加其轴力也在不断的增大，在土钉(锚杆)的末端轴力几乎为零，开挖过程中桩的轴力和剪力都在逐渐增大，桩身的最大剪力逐渐向下移动，上半部分桩的弯矩由小逐渐变大，而在下半部分，基坑底向下1m的范围内，弯矩值逐渐减小的支护结构的内力分布规律。

深基坑；数值模拟；支护结构；土钉；锚杆；桩

引言

随着我国城镇化的快速发展，城市人口剧增，城市的横向发展空间越来越少，迫切要求城市建筑朝纵向空间发展，这就促使我国高层建筑业的蓬勃发展。建筑高度不断增加促使基坑深度也随之相应地加深，这就对基坑支护技术提出了更高的要求。基坑支护尤其是深基坑支护的形式多种多样，常用的如大坡度放坡简易支护、土钉墙支护、锚杆复合土钉墙支护、桩锚联合支护、排桩内支撑联合支护等，各种支护形式均有其适用条件，应根据现场条件、地层情况、施工空间要求、经济性等因素进行综合选择，如采用内支撑的排桩支护结构占用基坑内面积较大因而对基础施工进度的影响较大，故基坑空间狭小的工程就不能采用此种支护形式。深基坑工程是岩土工程的热点问题，支护技术也成为亟待解决的问题。本文以土钉墙和桩锚联合支护结构为研究对象，采用FLAC3D数值模拟分析的方法，重点研究了土钉、护坡桩和锚杆等支护单元的受力规律，为该类支护结构优化设计提供依据[1-3]。

1 工程概况

该工程位于新乡市平原路与胜利路交叉口的东南角，建筑平面设计似倒“品”状，占地总面积5 047m2，建筑总面积9.3万m2，拟设三栋29层点式高层建筑构成倒“品”状排列，地下两层，基础埋深为自然地面下12m，地上总高98m。地下土层第1层：杂填土；第2层：粉质粘土；第3层：粉土；第4层：粉砂；第5层：细中砂；第6层：中砂。地下水位埋深5.7m左右，稳定水位埋深5.5m左右。水位年变幅2.0m左右，各土层参数如表1。

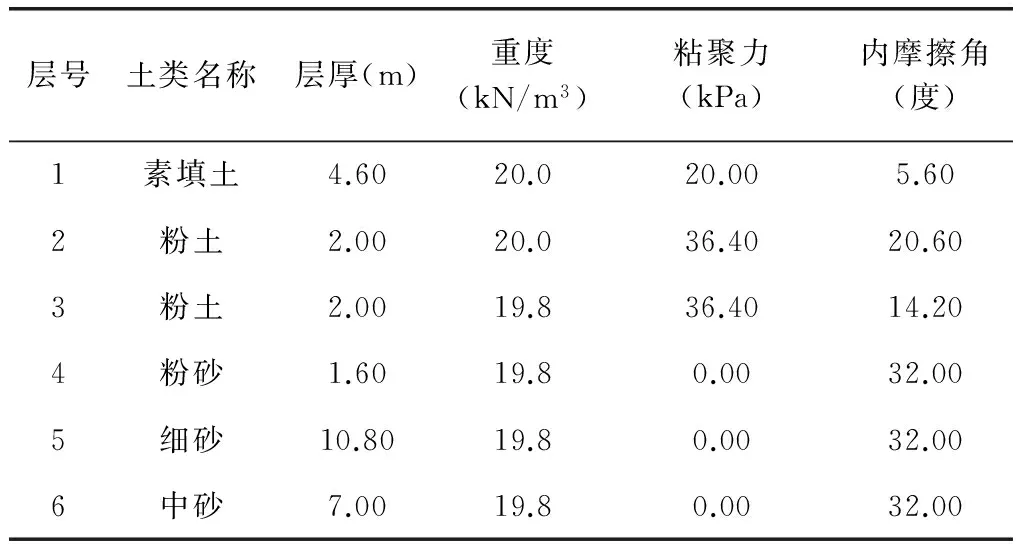
表1 各土层参数

基坑支护形式：自然地面以下5m范围内，按1：0.2放坡，采用土钉墙支护，上下和左右间距均为1.5m，土钉的布置正立面如图1所示；基坑自然地面以下5-12m范围内，采用桩锚联合支护结构支护，锚杆的布置正立面如图2所示。护坡桩采用钻孔灌注桩，桩径为600mm，桩中心距1 000mm，桩长为17m，桩顶以下设两排预应力锚杆，上下和左右间距均为2.0m，采用2根1860级(7ф5)钢绞线作为预应力筋，基坑支护剖面布置情况如图3所示。

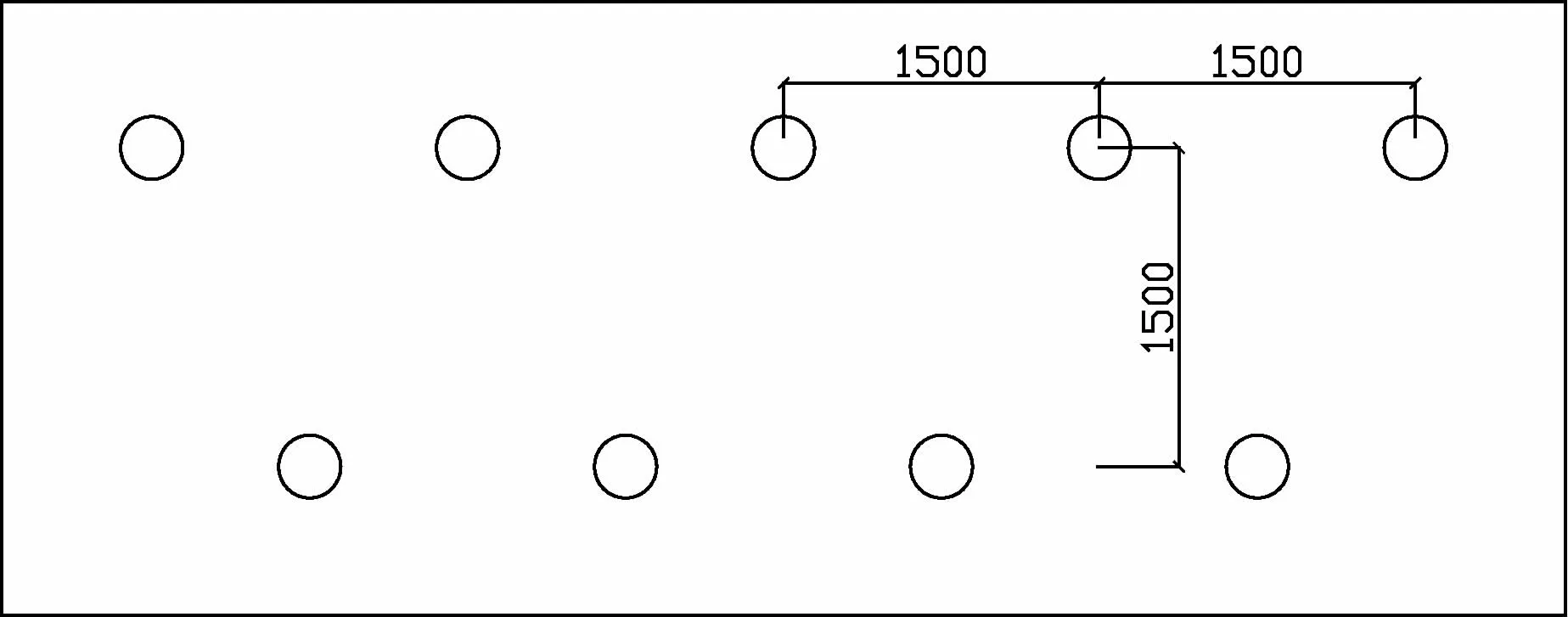
图1 5m以上土钉坡面正立面图

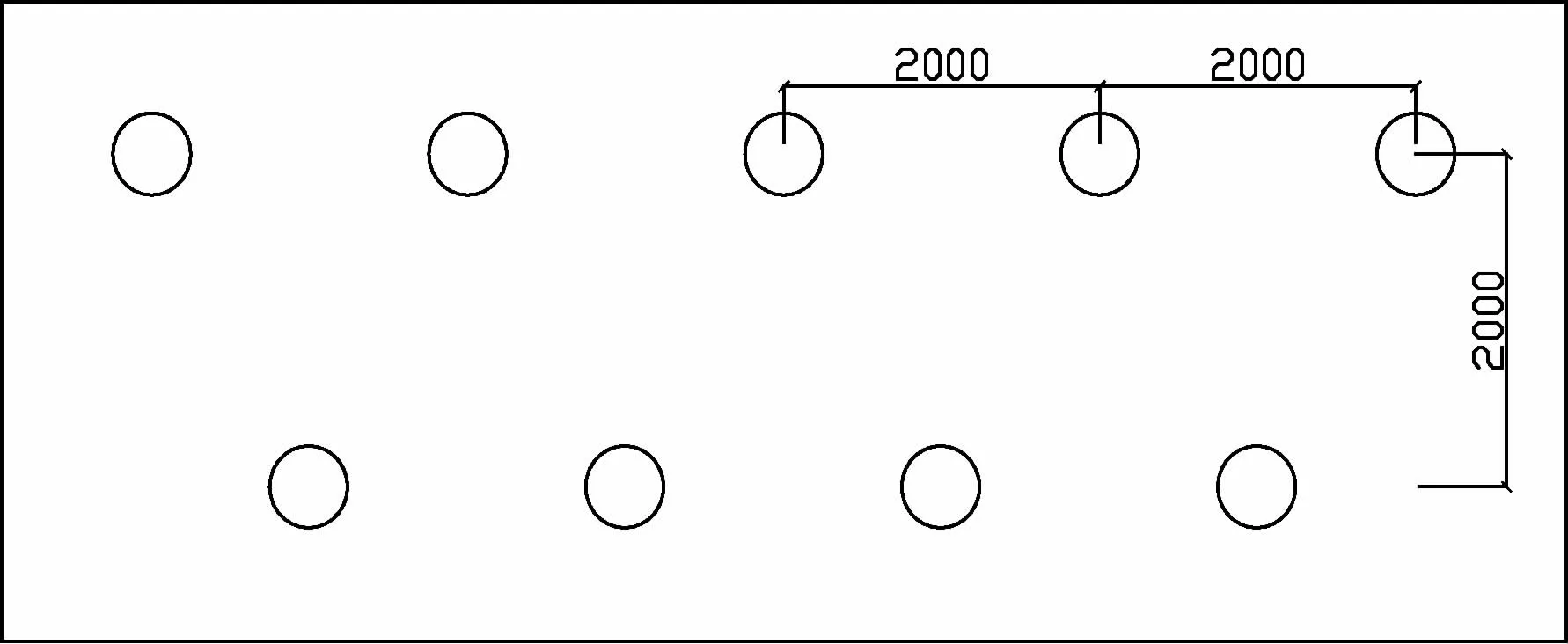
图2 5m以下锚杆坡面正立面图

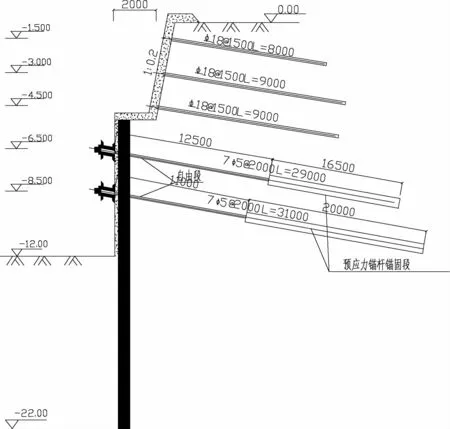
图3 基坑剖面图

2 支护结构受力情况分析

2.1 基本假定

为了便于建立分析模型，结合本工程的实际支护情况，做如下假定：

(1)土钉(锚杆)支护结构是平面应变问题；

(2)土钉(锚杆)与土体作用的锚固力由土体位移产生，若土体没有位移，土钉(锚杆)不受力；

(3)模拟的过程中，不考虑地下水影响，认为地下水位已满足要求(降水至开挖面以下)；

(4)不考虑土钉(锚杆)的横向抗剪作用；

(5)土钉(锚杆)与周围土体完全粘结，满足变形相容条件。

(6)钢筋和浆体为理想弹性体，周围土体理想弹塑性体，服从摩尔一库仑强度屈服准则；

(7)在开挖前，土体在自重状态下固结，开挖以前土体原位应力和性状的改变不予考虑；

(8)桩与周围土体完全粘结，满足变形相容条件；

(9)桩与冠梁是理想弹性体，周围土体为理想弹塑性体，服从摩尔一库仑强度屈服准则。

2.2 模型的建立

深基坑支护结构中的计算采用的是Mohr-Coulomb强度准则。在消除边界效应的原则下，充分考虑深基坑的具体形态特征、客观的工程水文地质条件和支护结构影响范围的情况下，建立计算模型。该模型的坐标系采用空间直角坐标系，xoy平面取为水平面，z轴为铅直方向。坐标系原点取在模型基底部，基坑底部开挖面边缘的正下方。边界条件的设置采用模型周边侧向约束，不允许水平方向位移，底面约束允许铅直方向变形，底面采用固定支座，四面采用可动支座。计算的影响范围垂直方向取为基坑开挖深度的2.5倍，水平向取为基坑开挖深度的4.2倍[4]。

本文利用FLAC3D建立分析模型，结合该工程的实际支护情况，模型的开挖分成6个步进行，本模型长50m、高30m、宽2m，开挖深度为12m；六步开挖分别为：第一步开挖2.0m，第二步开挖1.5m，第三步开挖1.5m，第四步开挖2.0m，第五步开挖2.0m，第六步开挖3.0m。土钉水平间距1.5m，第一排位于1.5m深处，垂直间距1.5m，第三排土钉距坑底7.5m，钻孔直径0.10m，第一排土钉长8m，第二排第三排土钉长均9.0m，倾角10°。护坡桩桩长17m。锚杆水平间距2.0m，第一排位于6.5m深处，垂直间距2.0m，第二排锚杆距坑底3.5m，钻孔直径0.15m，第一排锚杆长29m，第二排锚杆长31m，倾角15°，开挖支护后的模型如图4。

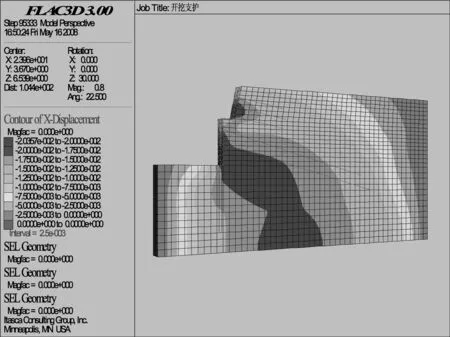
图4 三维模型和结构单元模型

模型由3 000个单元组成，模型采用摩尔-库仑强度准则，并假设其为大变形，因为大变形理论计算结果比小变形理论计算更精确[5-7]。结构单元认为是理想弹性体。

2.3 土钉和锚杆的内力分析

对在同一开挖深度不同土钉(锚杆)的内力分析：

(1)当土钉置入土体后，如果土体不变形土钉就不会受力。土体中土钉主要承受拉力，模拟得出的拉力呈两头小中间大的枣核形或抛物线状分布(图5，图7)，每排土钉的轴力值如图6和图8所示。

(2)图5是开挖第二步时土钉的轴力分布曲线，此时第一根土钉的轴力比第二根土钉的轴力大。最大值约10N，且土钉的末端轴力值基本为零，说明土钉在开挖至第三步时还没有完全发挥其作用。

(3)图7是开挖第三步时每排土钉的受力，由图可看出中间一排土钉轴力较大，第一排和最后一排土钉轴力较小，土钉两端的轴力值基本上为零或很小。

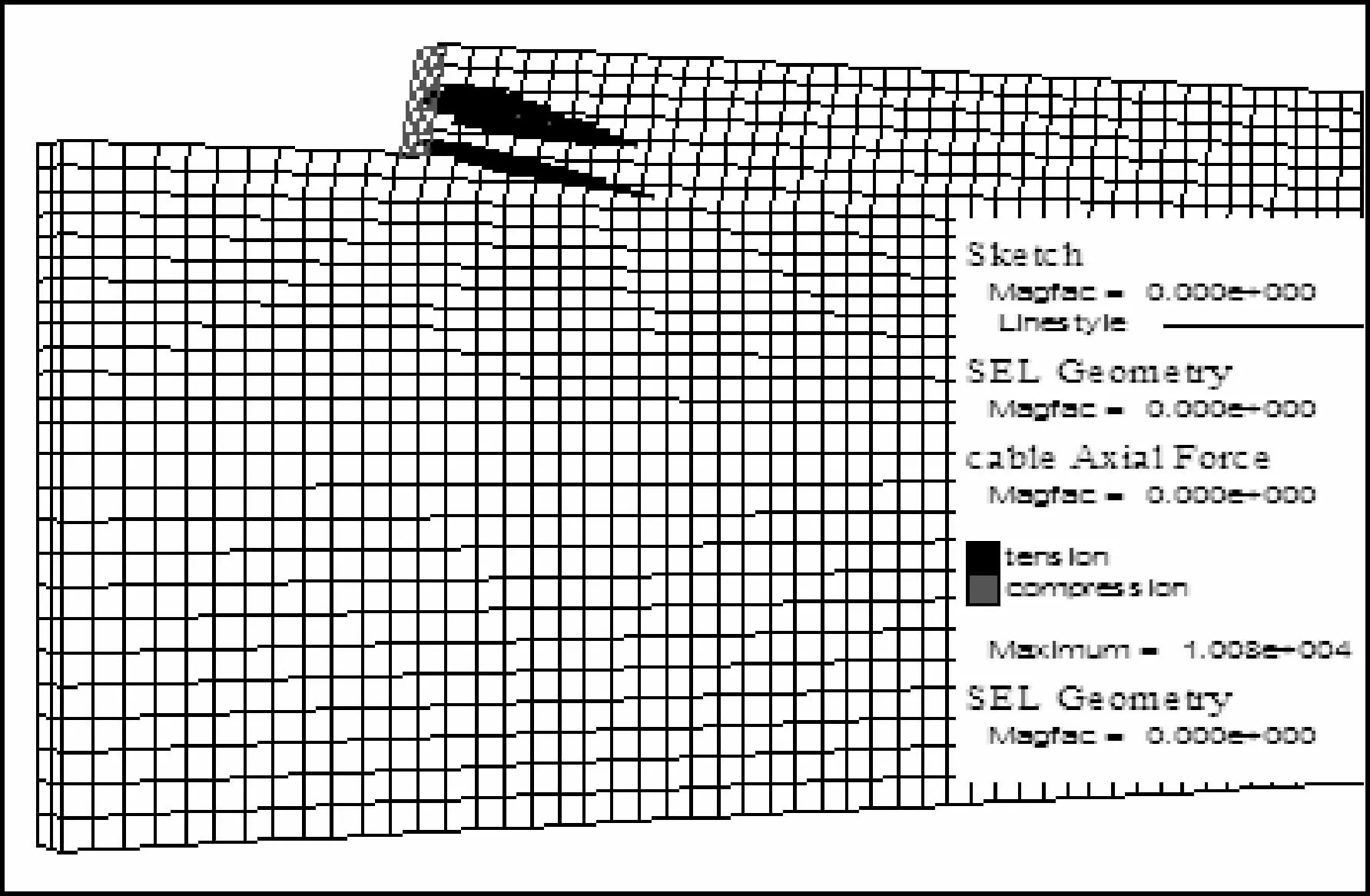
图5 开挖第二步土钉轴力图

(4)模拟结果中每排土钉轴力最大值自上往下逐渐向面层方向偏移，第一排土钉有所差异(图7)。第一排土钉的最大值接近中点靠左位置，最后一排大约在土钉长度的1/3处。各排土钉中第二排轴力最大，约为14kN，符合《建筑基坑支护技术规程》的要求[8]。根据文献[9-10]的研究，在加筋区的较上部分，最大土钉应力一般出现在土钉的中段或接近中间点的面层边。在加筋区的下部，最大拉力点较接近于移向土钉墙开挖面。

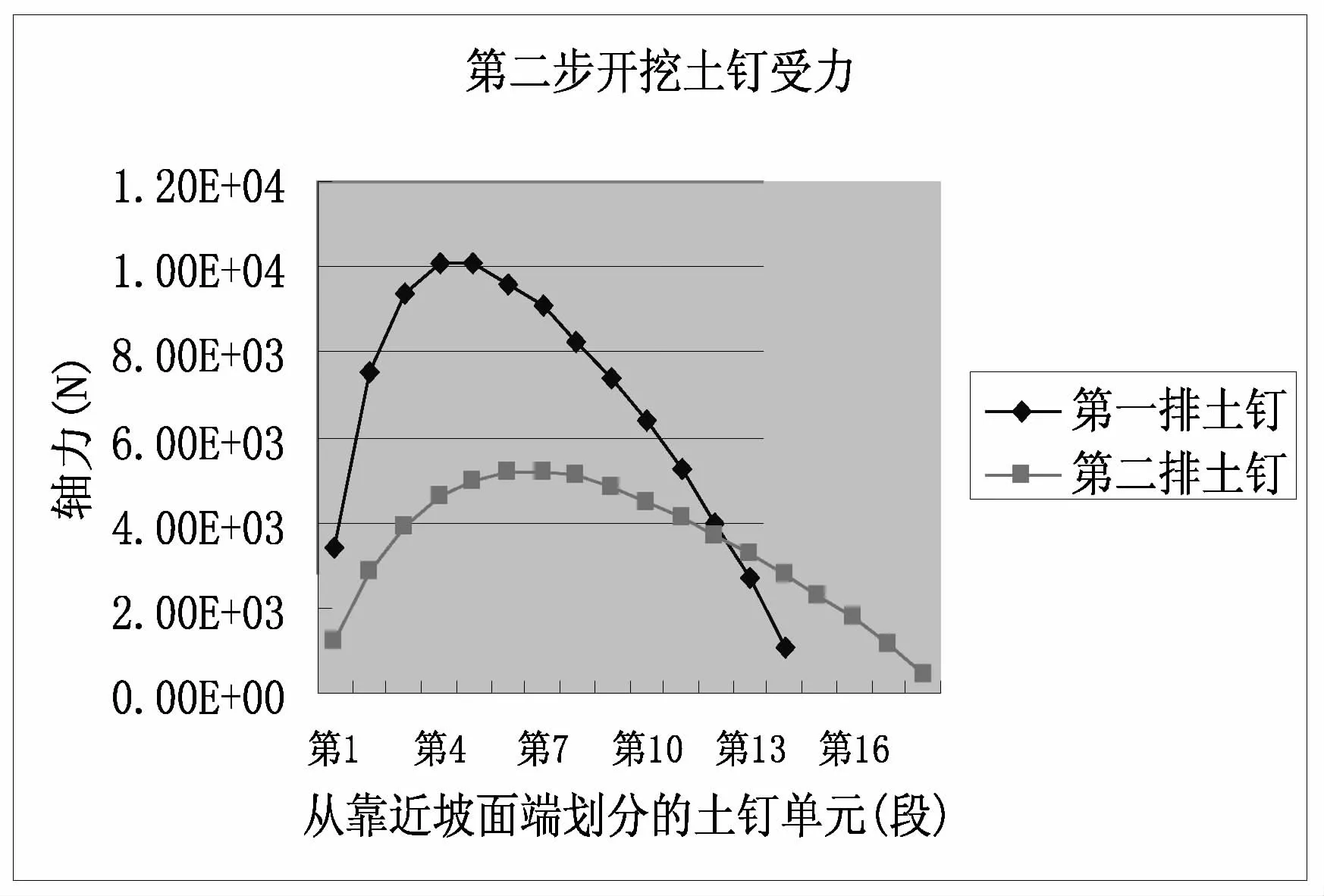
图6 开挖第二步土钉轴力分布曲线

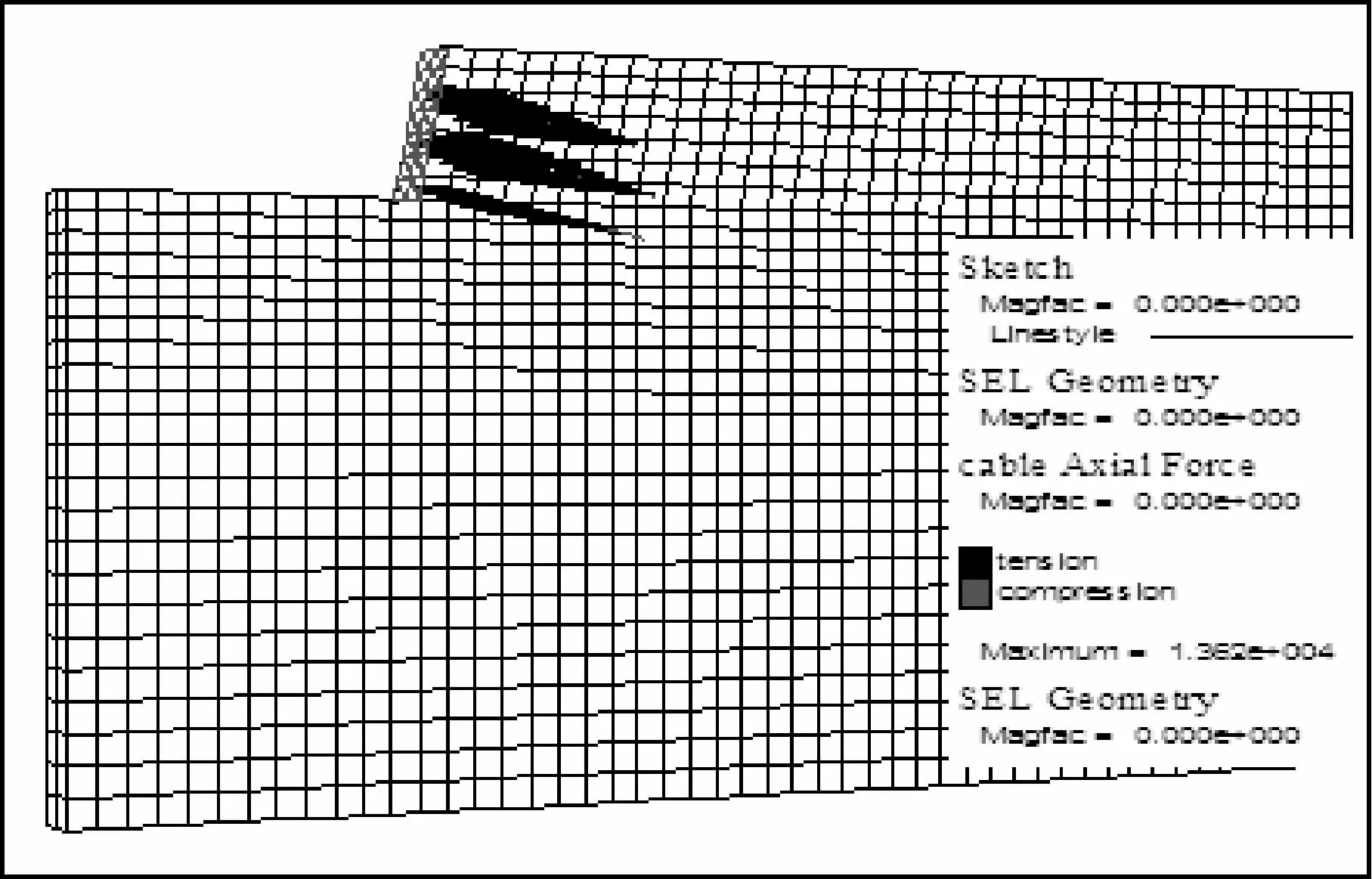
图7 开挖第三步土钉轴力图

图8 开挖第三步土钉轴力分布曲线

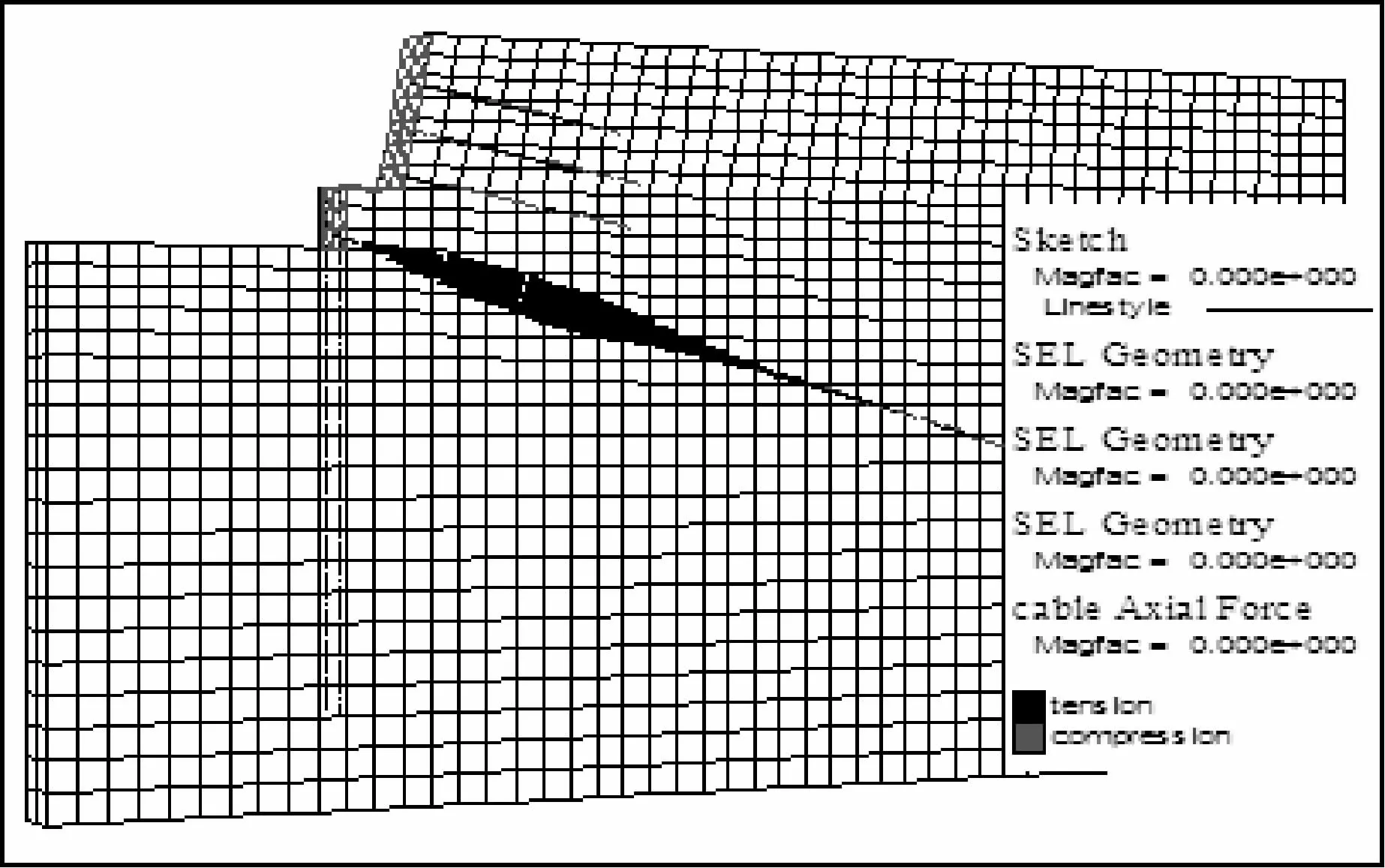
图9 开挖第四步锚杆轴力图

(5)土体中预应力锚杆主要承受拉力，模拟得出的拉力呈两头小中间大的枣核形或抛物线状分布(图9,11)，每排锚杆的轴力值如图10和图12所示。模拟结果中每排锚杆轴力最大值自上往下逐渐向面层方向偏移，图9显示第四步开挖时第一排锚杆的最大值接近中点靠左位置，且锚杆的末端轴力值基本为零，说明土钉在开挖至第四步时还没有完全发挥其作用。各排锚杆中第一排轴力最大，约为300kN，符合《建筑基坑支护技术规程》的要求[8]。图11反映在第六步开挖基坑稳定时锚杆受轴力分布也具有中间大两端小的特点，且锚杆得到充分利用，说明设计锚杆参数是合理的，基坑稳定。

(6)各排土钉(锚杆)轴力最大点的连线，就是边坡最小安全系数的滑动面，即基坑的潜在滑动面。

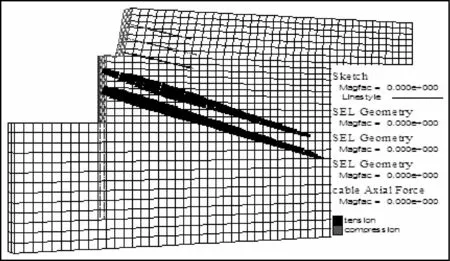
图11 开挖第六步锚杆轴力图

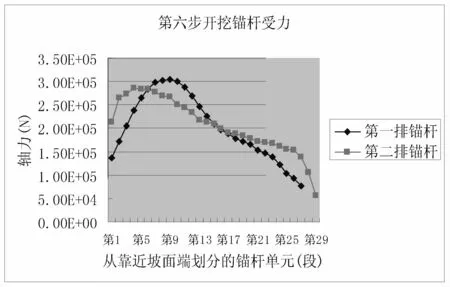
图12 开挖第六步锚杆轴力分布曲线

对不同开挖深度同一排土钉(锚杆)的内力分析：

(1)图13是第一排土钉在每步开挖支护后的土钉轴力分布曲线，可看出随着开挖深度的增加土钉的轴力逐渐变大。第一步开挖后最大轴力约为6.3kN，开挖第四步时最大轴力约为13.5kN。

(2)图14是第二排土钉在第二步至第四步开挖支护后的土钉轴力分布曲线，图中显示随着开挖深度的增加，土钉的轴力也是逐渐增大，第二步开挖时约为5kN，开挖第四步时突然增大至13.8kN。

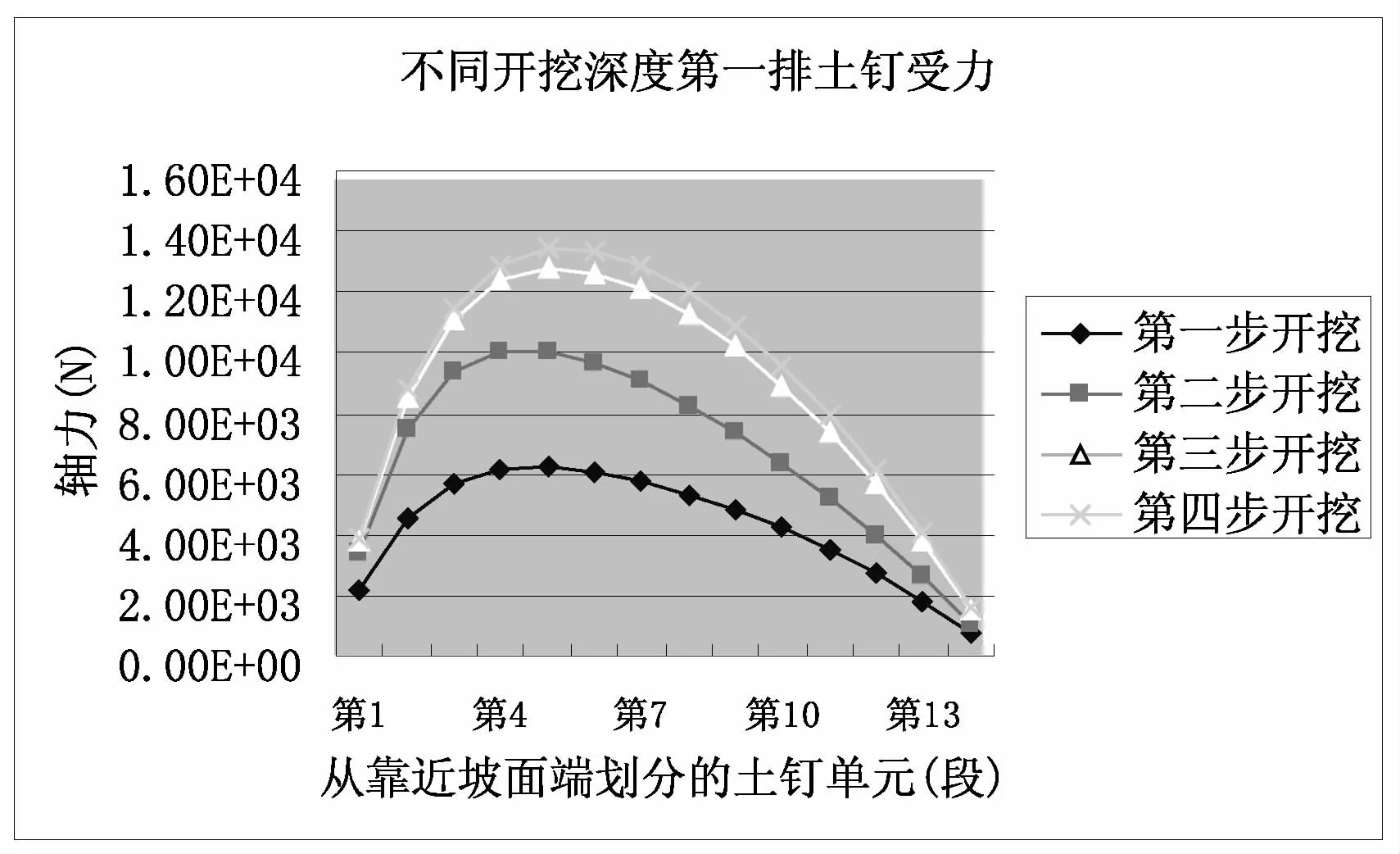
图13 不同开挖深度时第一根土钉的轴力分布曲线

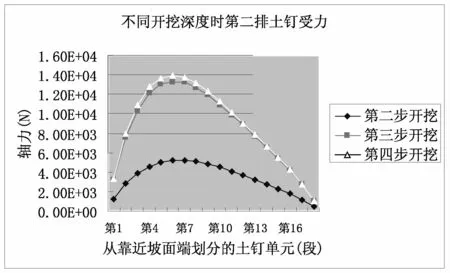
图14 不同开挖深度时第二根土钉的轴力分布曲线

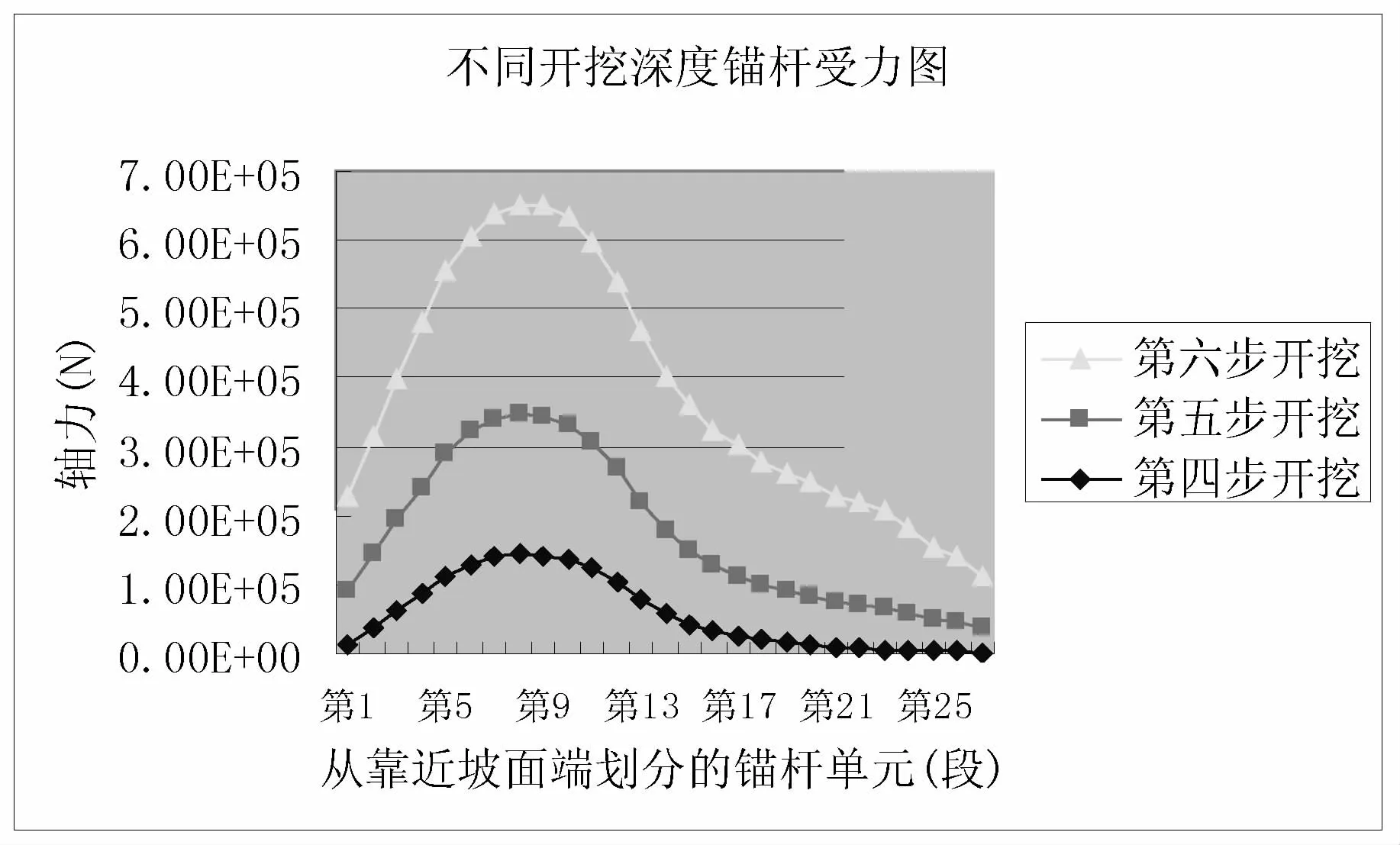
图15 不同开挖深度时第一根锚杆的轴力分布曲线

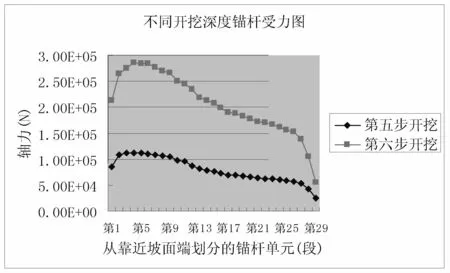
图16 不同开挖深度时第二根锚杆的轴力分布曲线

(3)图15是第一排锚杆在第四步至第六步开挖支护后的轴力分布曲线，可看出随着开挖深度的增加锚杆的轴力逐渐变大。第四步开挖后最大轴力约为150kN，开挖第六步时最大轴力约为300kN。图16是第二排锚杆在第五步至第六步开挖支护后的轴力分布曲线，可看出随着开挖深度的增加锚杆的轴力逐渐变大。第五步开挖后最大轴力约为120kN，开挖第六步时最大轴力约为280kN。

(4)由图13和图14对比分析知，在开挖过程中第一排土钉轴力的增长幅度没有第二排土钉的增长幅度大，且第二排土钉受力大于第一排。而有图15和图16对比可知，第一排的锚杆轴力要比第二排锚杆的轴力大，所以第一排锚杆起主要作用。由以上分析可知，随着开挖深度的增加，受拉土钉的轴向拉力增大，其原因是由于开挖深度越大，开挖面附近土体的位移越大，因此钉土表面的摩擦阻力增大，从而引起土钉的轴力随着开挖深度的增加而增大。土钉的轴向拉力基本上呈抛物线或枣核状，最大拉力点的位置也随着开挖深度的增加而后移。而对于锚杆开始在自由段施加预应力，随着开挖深度的增加其轴力也在不断的增大，由于预应力的存在使其与土体间产生摩阻力达到限制土体变形的目的。

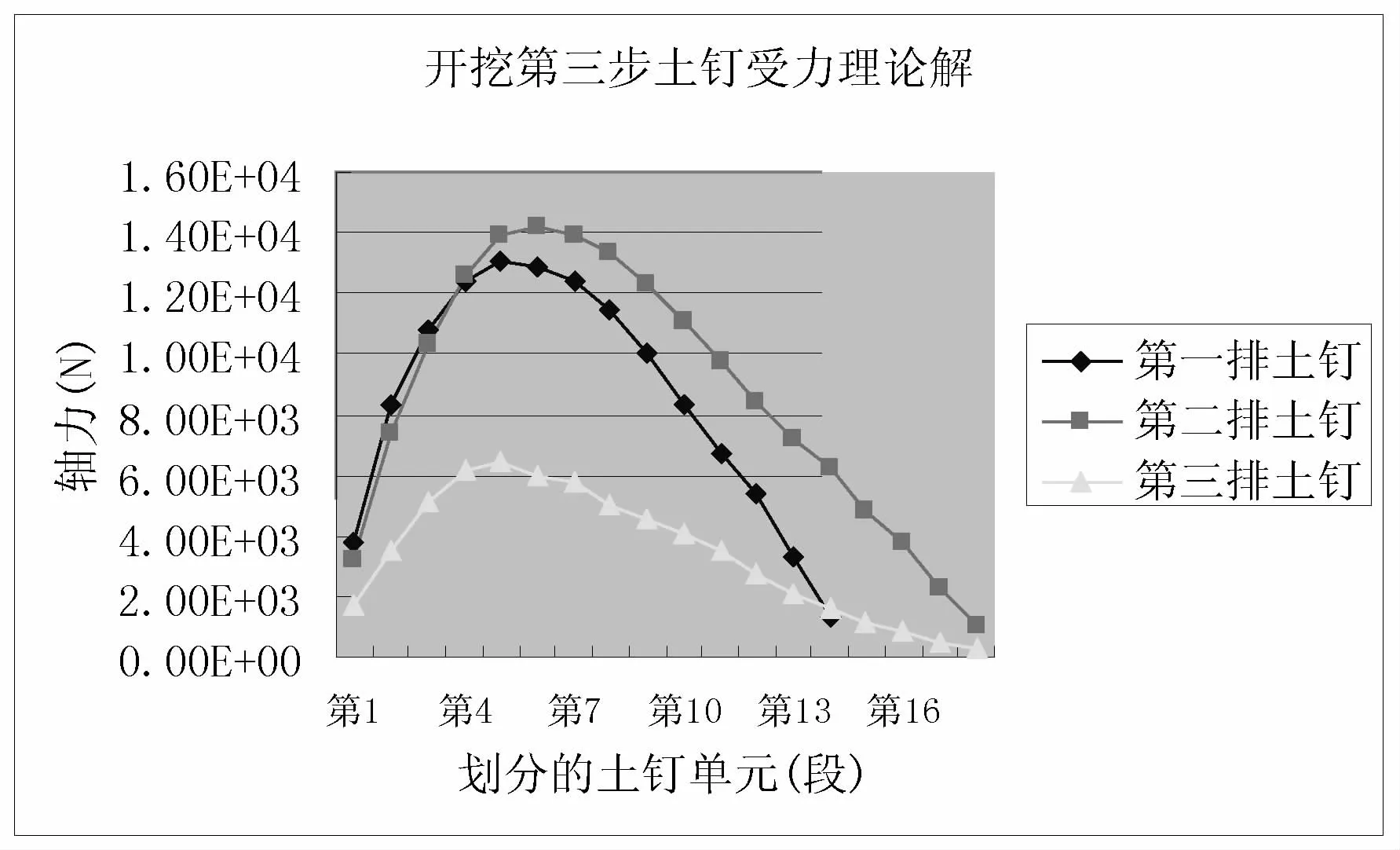
图17 土钉轴力的理论解分布曲线

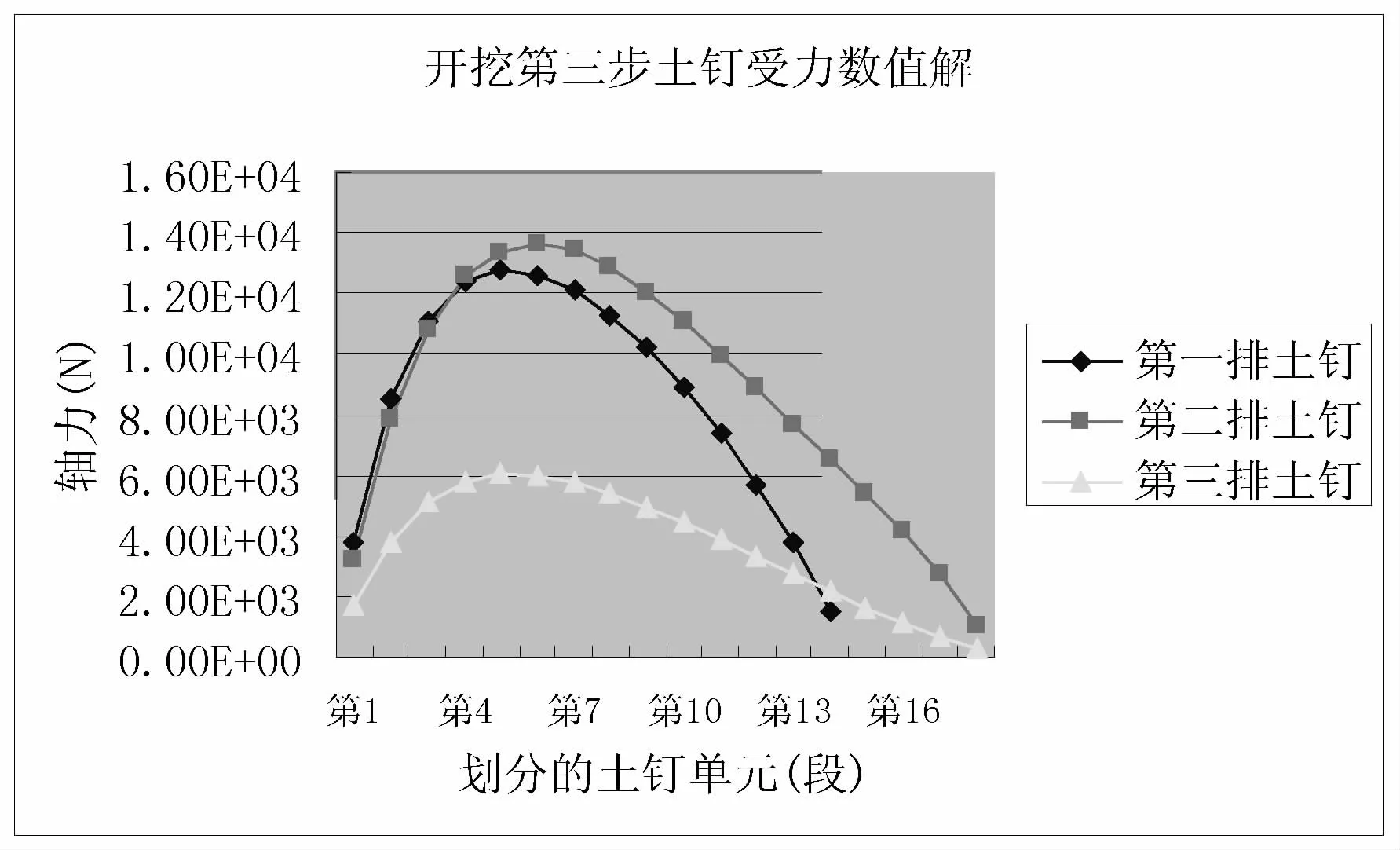
图18 土钉轴力的数值解分布曲线

图17-18和图19-20分别是开挖支护稳定后土钉轴力和锚杆轴力对比曲线，看出曲线基本吻合。模拟结果土钉和锚杆两端的轴力值很小，理论值比模拟值更小，几乎为零。另外，土钉和锚杆两端模拟得出的轴力值比理论公式得出的值稍大，中间部分模拟值比理论值小，但基本一致。

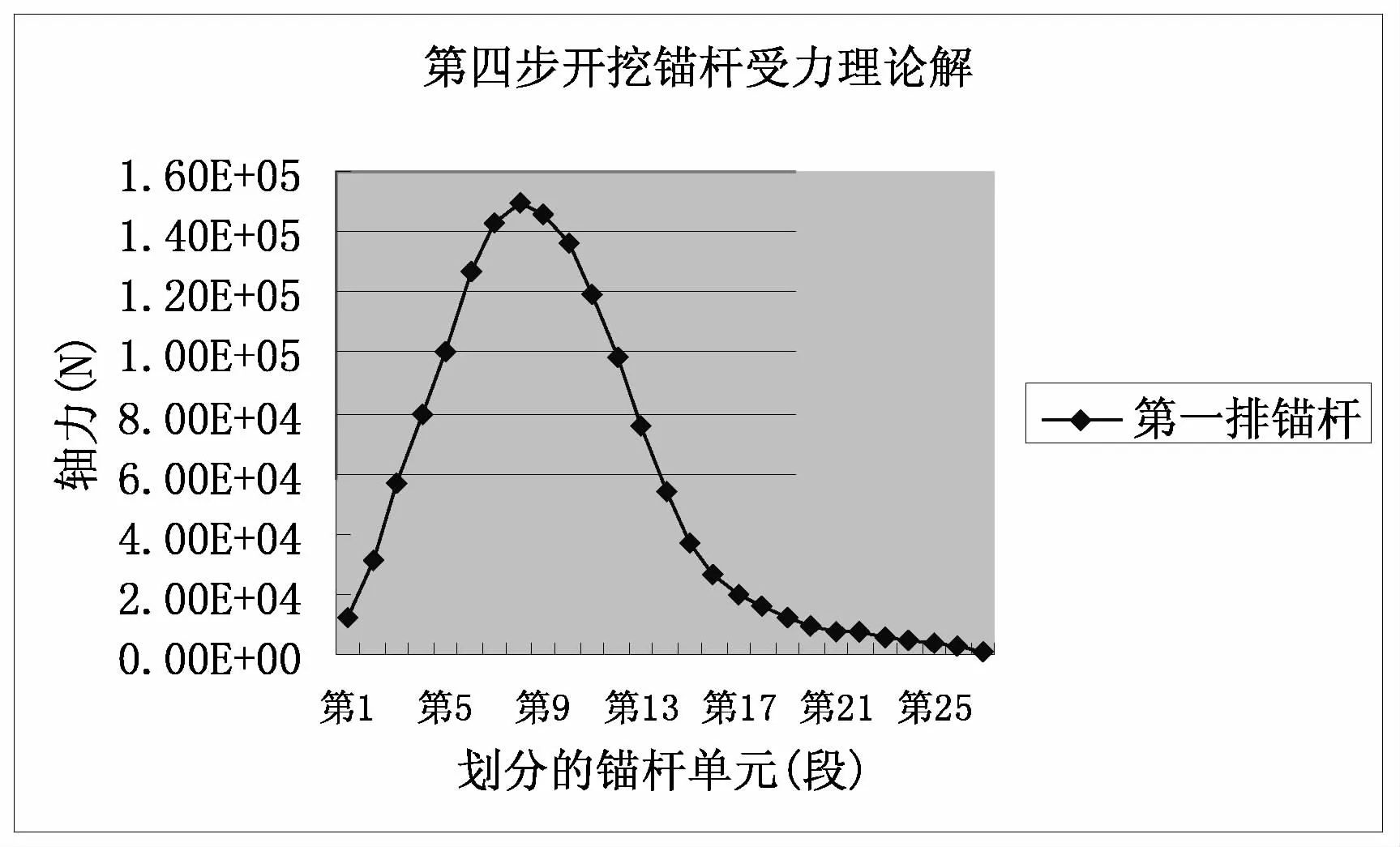
图19 第一排锚杆轴力的理论解分布曲线

由三排土钉轴力对比曲线可以看出，土钉两端的理论解小于数值解，在土钉的末端轴力几乎为零；在土钉中部理论解大于数值解。由理论公式解得第一排土钉的最大轴力为13.8kN，模拟得出的最大轴力为13kN，第三排土钉的最大轴力为6.2kN，模拟得出的最大轴力为6kN，均相差不大。数值模拟的计算结果虽大于实测值，但相差不是太大，而且计算出的内力分布规律与以往的研究成果所得出的结论基本一致，土钉轴向拉力位置与大小都基本吻合。

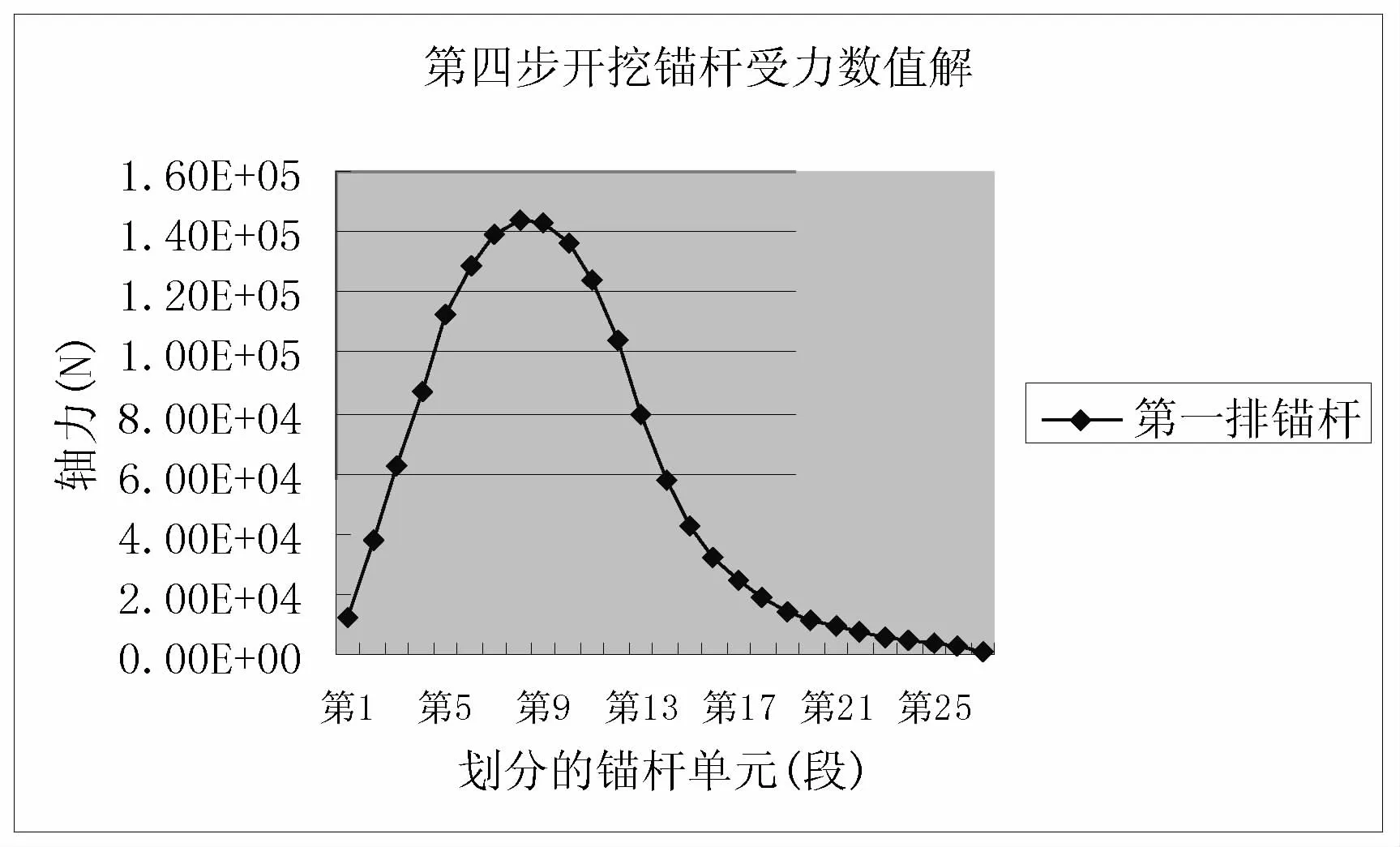
图20 第一排锚杆轴力的数值解分布曲线

同样由第一排锚杆轴力对比曲线可以看出，锚杆两端的理论解小于数值解，在土钉的末端轴力几乎为零；在土钉中部理论解大于数值解。由理论公式解得第一排土钉的最大轴力为150kN，模拟得出的最大轴力为145kN，相差也不大。数值模拟的计算结果虽大于实测值，但相差不是太大，而且计算出的内力分布规律与以往的研究成果所得出的结论基本一致，锚杆轴向拉力位置与大小都基本吻合。

数值模拟的计算值比实测值要大，这主要是由于建模过程中的简化而造成的，本文的方法计算出的结果比数值模拟的结果更大，是由于用了FLAC的计算值进行二次计算，导致误差累加造成的。

2.4 桩体受力分析

由上述不同开挖深度桩轴力对比图21可知，随着开挖的加深，桩的轴力逐渐增大；开挖完成后，桩身与坑底开挖底面处相交位置的轴力最大，往上和往下都比前一阶段的值小。随着基坑施工的进行，桩的轴力最大值逐渐向下推移，桩端处的轴力变化：小-大-小。

图21 不同开挖深度桩轴力分布曲线

由图22可知随着开挖的进行，桩顶处剪力逐渐增大，然后桩身的最大剪力逐渐向下移动。当开挖完后，此时桩身与坑底处交接处的剪力达到最大(见图22中的白线)，最大剪力值处向下1m的范围内，剪力突然降低，再往下桩身的剪力由大逐渐变小，甚至为零，然后到桩端有适当反弹。上部的开挖范围内，桩的剪力变化基本上是直线状。

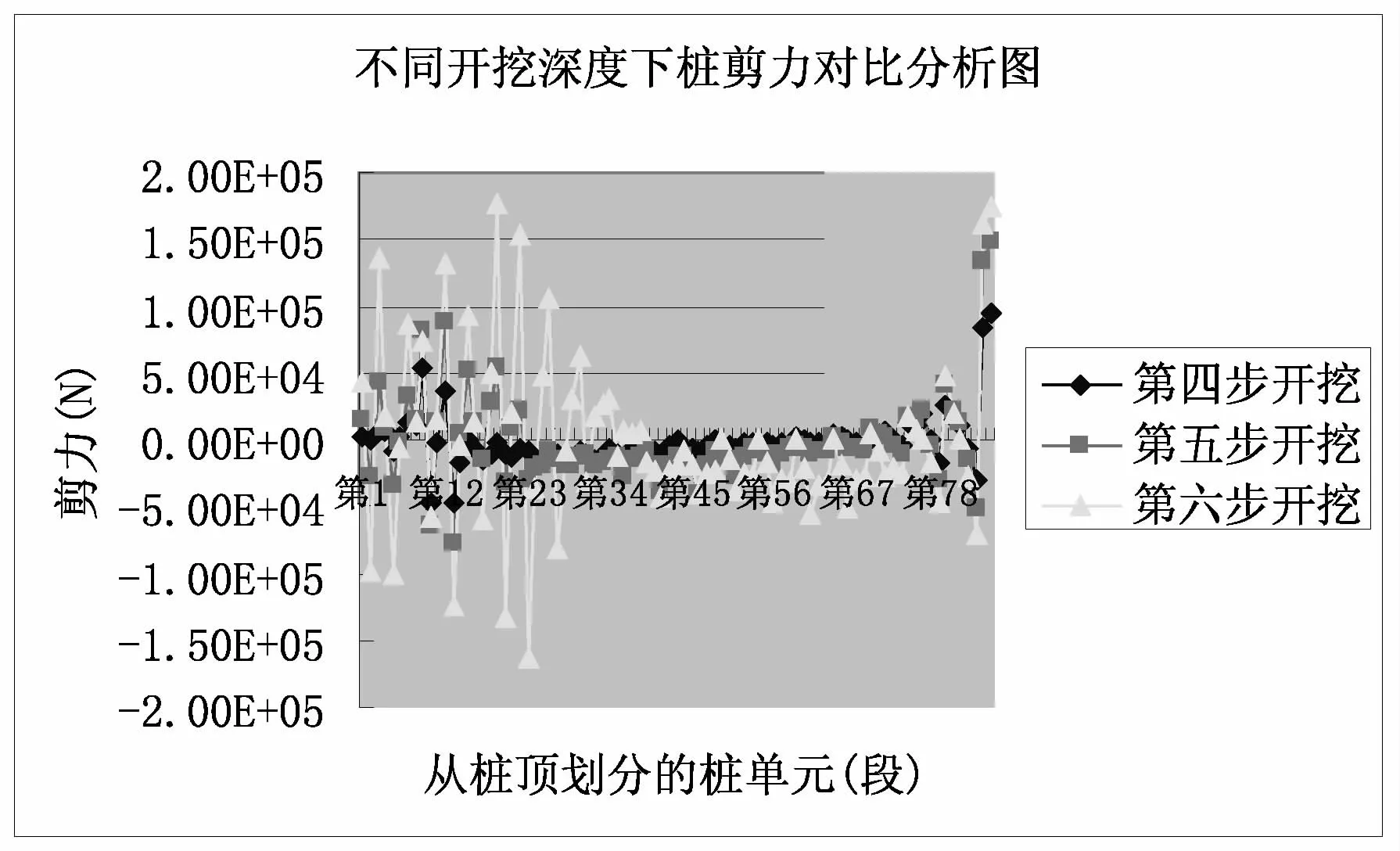
图22 不同开挖深度桩剪力分布曲线

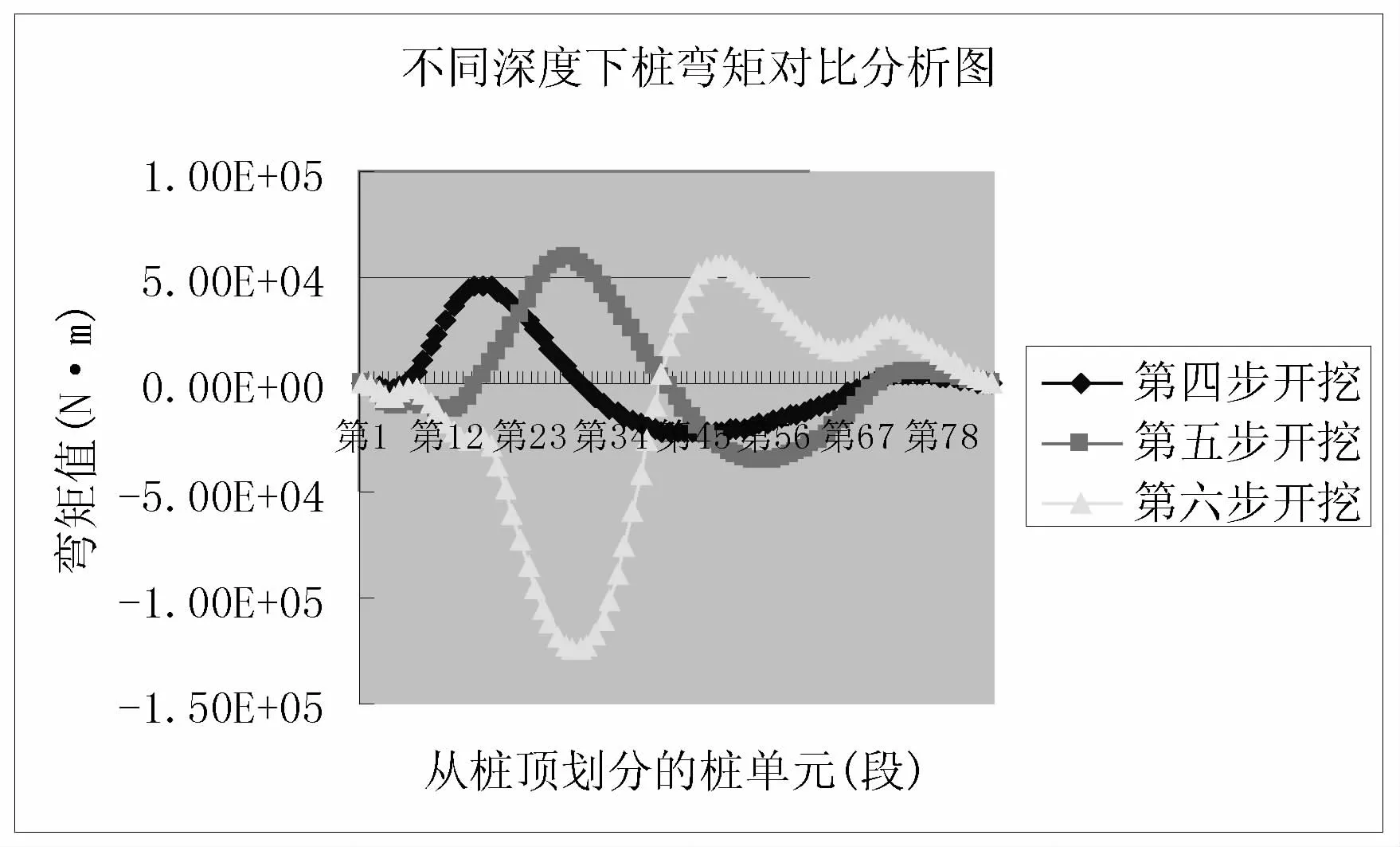
图23 不同开挖深度桩弯矩分布曲线

图23显示随着开挖深度的增加，上半部分桩的弯矩由小逐渐变大，逐渐增加到最大值；而在下半部分，基坑底向下1m的范围内，弯矩值是逐渐减小；当开挖完成时，桩身1/3处达到最大值。桩身弯矩的最大位置随基坑开挖有向下移动的趋势，在桩端处达到最小值。并且弯矩的零值点逐渐下移。当采用平衡理论设计时，正负弯矩相等时，桩横截面积达到最优化。因此桩的正负弯矩对桩结构的合理性有一定的影响。

3 结论

(1)通过理论上计算和数值上的模拟，从而得出了一系列关于基坑土体应力和支护结构的内力分布规律，土体中最大主应力、最小主应力均呈带状分布，其值是从上往下逐渐增加，对于土钉和锚杆所受内力呈“枣核”状或抛物线状分布，每排土钉轴力最大值自上往下逐渐向面层方向偏移。

(2)利用FLAC3D有限差分软件对基坑开挖过程进行模拟计算，对土钉、锚杆和桩的内力进行分析，根据计算数据做出受力曲线图，随着开挖深度的增加，受拉土钉的轴向拉力增大，其原因是由于开挖深度越大，开挖面附近土体的位移越大，因此土钉表面的摩擦阻力增大，从而引起土钉的轴力随着开挖深度的增加而增大。而对于锚杆开始在自由段施加预应力，随着开挖深度的增加其轴力也在不断的增大，由于预应力的存在使其与土体间产生摩阻力达到限制土体变形的目的，并与实测值以及理论计算值进行了对比分析，得出土钉(锚杆)两端的理论解小于数值解，在土钉(锚杆)的末端轴力几乎为零；在土钉(锚杆)中部理论解大于数值解，但相差不是太大，而且计算出的内力分布规律与以往的研究成果所得出的结论基本一致，说明本文所建立的模型是合理的。

(3)随着开挖的加深，桩的轴力逐渐增大，桩顶处剪力逐渐增大，然后桩身的最大剪力逐渐向下移动，上半部分桩的弯矩由小逐渐变大，而在下半部分，基坑底向下1m的范围内，弯矩值是逐渐减小。开挖完成后，桩身与坑底开挖底面处相交位置的轴力最大，往上和往下都比前一阶段的值小；且此时桩身与坑底处交接处的剪力达到最大，最大剪力值处向下1m的范围内；剪力突然降低，再往下桩身的剪力由大逐渐变小；所受弯矩在桩身1/3处达到最大值，在桩端处达到最小值。

[1]马平,申平,秦四清.深基坑桩锚与土钉墙联合支护的数值模拟[J].工程地质学报,2008,(03):401-408.

[2] 王立明,高广运,郭院成.考虑竖向土拱的桩锚与土钉的联合支护[J].岩土工程学报,2006,(z1):1481-1484.

[2] 陈肇元,崔京浩.土钉支护在基坑工程中的应用[M].北京:中国建筑工业出版社,2000.

[4] 刘波,韩彦辉(美国).FLAC原理、实例与应用指南[M],人民交通出版社.2005.

[5] 王广国,杜明芳,侯学渊.深基坑的大变形分析[J] ,岩石力学与工程学报,2000,19(4):509-512.

[6] 张心剑.土钉与桩锚复合支护方案设计方法探讨[J].探矿工程:岩土钻掘工程,2010,(11):39-41.

[7] 王远祥,汪永新.复合式围护结构在深基坑开挖中的应用及有限元分析[J].铁道建筑,2005,(06):56-59.

[8]《建筑基坑工程技术规范》YB 9258-97(冶金部).

[9] 郑刚,顾晓鲁.挡土结构古典内力计算方法的讨论[J],岩土力学,1999,20(2):67-70.

[10]黄强.深基坑支护设计技术[M].中国建材工业出版社.1995.5.

Study on Forces of Supporting Structures of the Soil Nailing Wall and Pile Anchor Combined Supporting System in Deep Foundation Pit

Cheng Yan1，Huang Zhiquan2，Gao Wen1

(1.ChinaAcademyofBuildingResearch,Beijing100013,China;2.NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450045,China)

Through the numerical calculation， this paper shows that soil nail and anchor rod internal force are “coefficient” shaped or parabola，and the maximum force of each row of soil nailing gradually shift towards the direction of the surface layer. With the increase of the depth of the excavation, soil nailing axial tension increases, and for the beginning of prestressed anchor free segment, along with the increase of the depth of the excavation,its axial force increases.The force of the end of the soil nail (anchor) is almost zero. Axial force and shear during excavation piles are gradually increased. The maximum shear pile move downward; the upper half part of the bending moment of pile is gradually increased. In the second half, under the range of 1m of the foundation pit, the moment value decreases the supporting structure of the internal force distribution.

Deep Foundation Pit; Numerical Modeling; Supporting Structure; Soil Nailing; Anchor; Pile

程岩(1983-)，男，博士，工程师。主要研究方向：地基与基础工程，边坡与基坑工程。

TU473·2；TU94+2

A

1674-7461(2015)02-0073-07