善用错解资源生成高效课堂*
☉江苏省溧水高级中学 李宽珍
善用错解资源生成高效课堂*
☉江苏省溧水高级中学 李宽珍
学生出现错误是参与学习的一种必然现象,教师对此通常采用的处理方法是:不管不顾;或不分析错误,直接印发答案;或在课堂上重点讲评学生的错误,并给出正确答案,甚至给出多种解法,但不注意去分析学生错误的原因,如知识、技能的缺陷,思维的片面等.这些做法都不利于学生的思维能力的形成、提高和优化.学生在解题中出错是学生学习活动中的必然现象,老师因势利导,剖析错因,鼓励学生讨论、探究和纠正,善用错解资源,生成动态课堂,必能促进有效教学.下面笔者结合平时的教学实践谈谈如何利用错解生成有效课堂.
一、善用错解资源,引入新课
针对学生在学习中遇到的错误,教师不能全盘否定,可以充分利用,发现错解中的价值.在上课开始时巧设“误区”,让学生从“错误”中启航,一路探索,在与错误的不断碰撞中获取新知、增长才干.
案例1:在学习“数系的扩充与复数”前,笔者先让学生做一个简单的练习:
学生大惊!这个值怎么会是负值呢?题错了吗?方法就是平时的化归思想,没有问题啊!怎么回事呢?这时候教师不要急于指出一些学生的错误,而是鼓励学生在听课过程中自己寻找问题的答案.有学生尝试去解方程:,发现这个方程竟无实数解!这样一下子就激发了学生的学习兴趣和求知欲,使学生在极短的时间内迅速进入学习的最佳状态.学生面面相觑,全部转向教者,于是点题,自然而富有悬念地引入新课.等到学生在课堂上掌握了复数知识后,自然会豁然开朗,体验成功的快乐.
巧妙地利用学生的“错误”良机,能让学生产生认知上的需求,从而积极主动地投入到课堂教学中.在知识逐步完善的过程中,学生不断修正自己的认识,最终自己改正错误.这种教学方式比教师直接将知识硬塞给学生,更能让学生愉快地接受,效果自然也好得多.
二、善用错解资源,调整课堂
由于学生的认知水平、思维方式等方面存在着差异,因而课堂生成难免存在一定的偏颇和失误.教师要树立正确的“错误”观,鼓励学生发言,给学生犯错的机会,并有效地利用学生的错误,引导学生质疑、讨论、探究,促使学生通过比较、分析、反思,获得从失败走向成功的体验,提高对错误的“免疫力”.
案例2:在半径为1的圆上随机地取两点,连成一条弦,则其长超过圆的内接等边三角形的边长的概率是多少?
教师先让学生独立解决,然后交流成果.
生1:记事件A={弦长超过圆内接等边三角形的边长},如图1,取圆内接等边三角形BCD的顶点B为弦的一个端点,当另一点在劣弧CD上时,|BE|>|BC|,而弧CD的弧长是圆周长的,故由几何概型公式得
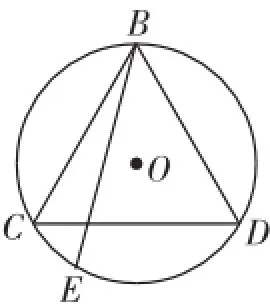
图1
生2:我是过点B作射线,求射线与弧CD相交时的概率.射线绕点B转一圈为2π,而与弧CD相交时转动的弧
不少同学觉得两种解法都有道理,但为什么结论不一样?究竟谁对谁错?
矛盾激起问题的波澜,引起了学生思维的碰撞,课堂开始热闹起来.教师决定利用这预设外的“错误资源”,引导学生讨论辨析.
生3:生2作射线不对,因为射线可能与圆没有交点.生1的解法是正确的.
师:生2的思考方法是可行的,但要借助条件概率才能解决,即求过点B的射线与圆相交的前提下与弧CD相交的概率.这部分内容将在选修2-3中学习.在几何概型公式计算中,主要体现空间测度的计算,即随机事件A发生的概率为(D的测度不为0).其中“测度”的意义由D确定,当D分别为线段、平面图形和立体图形时,相应的“测度”分别为长度、面积和体积.
错误是在教学过程中动态生成的,是可遇而不可求的,教师要善于利用“错误资源”,寻找错误背后隐含的教育价值,使之成为新的教学契机.通过相互交流,深层探究,使学生在正确与错误的矛盾中激起思维碰撞,引发知错、改错、防错的良性反应,并从中审视与体验,从而帮助学生建构起正确的认知结构,对数学学习产生积极的情感体验.数学课堂正是因“错误—发现—探究—归真”的良性循环而灵动充溢.
因此,教师可以抓住学生学习过程中一些可以利用的“错误”,鼓励学生通过自行修改题目从而保留“错误”答案.用这种方式处理学生的“错误”,一方面可以保护出错学生的自尊心,调动学生的学习积极性,另一方面,这种独特的变式训练可以有效地活跃学生的思维,使学生在“错误”中内化知识.
三、善用错解资源,深化课堂
在平时的教学中,教师应该关注学生的生成,而且有一定的调控意识.课堂上可以诱使学生犯错,或者有意识地展示学生的一些错误解法,让学生充分暴露其知识漏洞和思维偏差,从而针对学生的问题,揭示问题的本质,提高教学的有效性.
案例3:已知锐角△ABC中,a=2bsinA,求:
(1)B的大小;
(2)cosA+sinC的取值范围.
课前笔者搜集、整理试卷上出现的两种典型错误,展示给学生,课堂上要求学生分析、交流讨论,找出问题的症结.如果你认为正确,那么你要给出正确的理由;如果你认为错误,那么你要给出错误的原因.
错解展示:(2)解法1:cosA+sinC=cosA+sin(A+B)=
师:他们做得对不对?如果不对,那么这种解法有合理的地方吗?问题出在哪儿?你能帮助改正吗?
学生通过比较、讨论,总结出:都用到诱导公式、两角和的正、余弦公式将二元问题转化为一元函数的值域问题,再通过角的范围求解.只是解法1在用辅助角公式时将两角和的余弦公式记错了!解法2应该是正确答案!
师:解法2没有问题吗?再审读题目,看看条件有没有利用充分!
学生再次沉思,很快有了想法:第二种解法也错了——两种解法角A的范围都错了!角A的范围是而不是
师:为什么?
生5:锐角三角形的充要条件是每个角均是锐角,将角C也用A表示出来,可求得A的范围.
师:很好!本题出错的关键在确定角的范围时,各个角之间是有联系的,要保证每个角都是锐角!不能忽视这个隐含条件,这是我们常见的典型错误.
从两种错误的解法中,学生学会了将多元问题转化为一元问题的常用方法——消元法;从两种错误解法的辨析和改正中,了解了挖掘隐含条件的方法——深刻理解概念,将概念的内涵用外显的式子表达,不能遗漏.
学生的作业、试卷中往往存在诸多错误,当一些关键性的、有普遍意义的错误,被老师及时捕捉并经提炼成为全班学生新的学习资源,再及时而适度地对学生进行引导时,“错误”才可以更好地促进学生的认知能力,帮助学生从对错误的反思中,提高对错误的判断能力,揭示问题的本质,从而能深化课堂,提高课堂的有效性.
四、善用错解资源,反思课堂
《高中数学新课程标准》指出:学生的数学学习活动不应只限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.这些方式有助于发挥学生学习的主动性,使学生的学习过程成为在教师引导下的“再创造”过程.课堂上学生的“错误”很有可能就是一次激发学生进行探究的机会,在课堂上有时故意留点疑问,露点破绽,反而能促进学生认真听讲,反思课堂,更有利于学生对知识的理解与掌握.
案例4:已知a、b∈R+,且a+2b=1,求的最小值.
通过学生的解答,展示几种典型错误解法.
解法1:由a、b∈R+,得两式相加,得
通过上面四种解法的比较和正误的辨别,使学生发现这样一个问题:运用公式a+b≥2时等号成立应当是有条件的,而这也正是利用基本不等式求最值容易出错的地方.
通过利用学生的“错误”,使整个课堂进入一个“思考、探究、获得”的良性循环,学生在自主探究中找到学习的乐趣,成为学习的主人.
学生不出错的课堂,不是真正的课堂,学生不出错的教学,不是真正的教学.“人非圣贤,孰能无过.”更何况“学生的错误都是有价值的(布鲁纳)”.作为教师的我们,要在课堂上抓住学生“错误”的时机,巧妙、合理地处理好学生的“错误”这一教学资源,从学生的认知规律出发,正确引导对错误的分析评价,从纠错中体验快乐和成功,使我们的课堂更加真实、灵动、精彩.A
*本文是南京市“十二五”规划课题《利用错题集培养高中学生反思能力的策略研究》的阶段性成果,课题编号:L/2013/039.

