新课程建构模式下的试题讲评初探

☉浙江省余姚市第二中学 杨福来

新课程建构模式下的试题讲评初探

☉浙江省余姚市第二中学 杨福来

众所周知，数学教学是概念教学—新知教学—解题教学—反馈教学—反思教学等一系列系统的教学综合．对整个高考应试而言，学生更直接领会的是解题教学的好坏，这就要求教师在解题教学中准确实施试题讲评．在国内著名的数学论坛K12或百度贴吧里，笔者常常看到学生的抱怨：我们的老师讲什么都不知道，明明很简单的问题讲的方法又繁又复杂！老师讲的方法我听懂了，可是我们根本想不到！怎么破？……这就表明了解题教学中很重要的一个问题：教师在试题讲评的时候如何做到以生为本？试题讲评如何在新课程理念下让学生积极参与？如何在传统的试题讲评基础上做到螺旋式上升？笔者认为，这是教师关于试题分析教学部分一个值得全新研究的视角．

课程标准的理念一直致力于学生的自主探索和积极建构，其特别提到了数学教学如何尽可能地去形式化，如何通过对特殊情形的认知到达一般化的归纳，如何渗透主动建构知识体系的操作等.从近年的新课程教学来看，在概念教学、新知教学等方面我们做出了很多类似的尝试和探索，在各种公开课中也聆听了许多这样的探求．但是笔者思考：似乎在复习课、解题课、试题分析课等环节，教师对新课程理念的合理运用和渗透并不如新知教学那么普遍，这一点很多教师都有共识．究其原因，笔者认为有三：其一，试题讲评、复习教学等课程的设计不如新知教学方便，尤其在利用情境手段引导学生发现、挖掘情境背后的形式化结果方面，试题讲评、复习教学难度较大，这也是此类课开设不够普遍的原因；其二，教师自身的观念限制和能力限制，我们知道教师在解决问题时存在知识主观的熟练程度和习惯不同，造成了其解决问题往往从自身思考角度入手，有时这种思考角度并非是学生能够入手的思考方向和着力点，致使试题讲评未能缘自学生的思维发展区出发，有些事半功倍；其三，观念的更新，新课程一直提倡教师专业化的成长，而不再是做一个普普通通的教书匠混日子，要有更出色的教学能力和授课水平，必须在学生最为重视的试题分析上做到潜心研究，提高自身专业化的发展．陕西师大罗增儒教授在关于如何解题、析题时说：当下数学教学的核心依旧是解题教学，因此试题的分析能力、解决问题的能力是辨别教师水平最直接的体现，我建议要用新的方式、方法去引导中学生解决数学问题，这里的方法可以是一题多解、启发式讲学、错题辨析等多种不同的手段进行尝试．本文鉴于上述缘由和数学解题教学泰斗罗教授的分析，从试题分析多种方式的探索，结合新课程理念做了一些初探，与大家交流．

一、花出深谷，其香尤浓——学生思维视角讲评

解决某个数学问题有很多方法，教师在试题解决过程中首要考虑的是方法的简便性、运算复杂程度等，有时正是因为考虑上述环节过多导致忽视了学生解决问题的心理机制.我们常常有这样的感受：教师将自己的方式、方法在黑板上积极板演，讲得头头是道，最后学生往往没有吸收进去，而且其自己的方法也没有弄明白，这样的试题讲评是低效的、无效的．尊崇新课程理念，笔者认为试题讲评还需要从学生的学情出发，首先通过批阅查看学生对解题方法使用的分布率，其次是思考学生为何会产生如此的想法解决问题，最后是通过学生思维的视角与学生一起分析试题、解决试题，这样的教学是有生命力的，符合学生看问题的角度，符合新课程鼓励学生探索、积极建构方法解决问题的理念．

案例1：如图1，过x轴上一动点A（a，0）引抛物线y=x2+1的两条切线AP、AQ，P、Q为切点，设切线AP、AQ的斜率分别为k1和k2．

（1）求证：k1k2=-4；

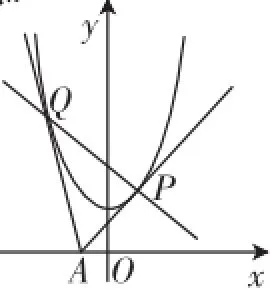
图1

（2）试问：直线PQ是否经过定点？若是，求出该定点的坐标；若不是，请说明理由.

说明：本题是解析几何中直线与抛物线位置关系的一种典型问题，考查了抛物线的切线、动直线过定点的问题.笔者将本题布置为某次作业，在批阅过程中发现学生解决问题的思维视角与教师的想法有些出入，因此笔者研究学生对于本问题的解答思路后进行了课堂试题的学生视角讲评.

第一问讲评如下所示.

本题是研究抛物线的切线，考虑到还未对导数进行授课，因此导数知识运用暂不予考虑.

学生视角讲评1：设过A（a，0）与抛物线y=x2+1相切的直线的斜率是k，则该切线的方程为：y=k（x-a）.

学生视角讲评2：设点P（x1，y1）、Q（x2，y2），在这两点处的切线分别为l1、l2.设l1：y-y1=k1（x-x1）.由

由题意知l1、l2交于点A（a，0），所以

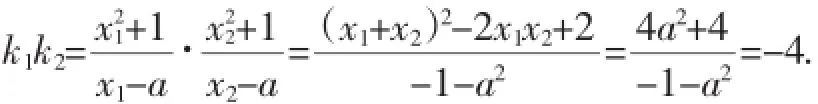
学生视角讲评3：设过A（a，0）与抛物线y=x2+1相切的直线的斜率是k，则该切线的方程为：y=k（x-a）.

说明：为何讲评第一问的解法呢？笔者发现：学生对于相切的认知永远是最直白的接受和表达——Δ=0，对根的认知也非常直接——求根公式求之，因此讲评1是最尊崇学生思维角度的讲评，也是最容易靠拢学生思维的讲评；讲评2借鉴了通过导数求抛物线的切线方程的思想，通过设切点坐标，联立方程后的判别式为0，从而得到切线方程的斜率，计算量较大，但是为解决第二问做好了充分的准备；讲评3是仅有的少数优秀学生的视角，但应该是本题最简化的视角，教师应该将这一优秀学生的视角予以呈现，用韦达定理解之是本问题最简捷的方向.

第二问讲评如下所示.

研究直线过定点是如何实现的？从最基本的知识可以知道，带有一个参变量的直线方程可以研究其过定点，因此讲评的核心是如何将直线PQ表示为关于变量a的直线.在学生解决的过程中，笔者整理了三种不同的方式予以讲评.

学生视角讲评3：设P（x1，y1）、Q（x2，y2），故切线AP的方程是，切线AQ的方程是又由于A点在AP、AQ上，则y2=2x2a+2，则直线PQ的方程是y=2ax+2，则直线PQ过定点（0，2）.

说明：通过批阅发现，学生解决本题最易想到的视角是利用设点—求斜率—写出直线—研究定点，因此视角1与视角2都是按照学生在阅卷中的想法进行的讲评，视角3只有少数优秀学生考虑使用，其合理地借鉴了“过圆外一点作两条切线，则两切点连线所在的直线方程”的推导过程进行了类比处理，是思维较为高端抽象的一种体现，教师讲评视角3是为了提携学生站在更为抽象、有高度的角度看问题．

二、探索建构，悠然自得——启发引导视角讲评

在突出学生解决问题方面，笔者认为要加强学生问题解决的探索能力的培养，在试题讲评中引入学生探索、建构、讲评，将试题讲评交还给学生，使其真正领悟到讲清楚问题比会解问题更容易将知识在自身体系中完善起来．看一个案例.

案例2：设命题p：方程（m-6）x2+（m+6）y2=1表示双曲线；命题q：方程x2+y2-2x+4y+m=0表示的曲线是圆．

（1）当m=5时，判断命题“p且q”的真假，并说明理由；

（2）若命题“p或q”为真命题，求实数m的取值范围．

说明：本题是笔者给予学生讲评尝试的一道数学问题，主要是请学生研究了第二问，从逻辑认知的角度使其认清楚“或”结构的命题是如何讲评的，请学生探索建构．

学生探索建构1：我认为，若命题p为真命题，则-6＜m＜6，若命题p为假命题，则m≤-6或m≥6；若命题q为真命题，则m＜5，若命题q为假命题，则m≥5.因为命题“p或q”为真命题，所以分p真且q假，或p假且q真，或p真且q真三种情况，即解得m＜6．

学生探索建构2：我认为可以从反面认知本问题.若命题“p或q”为假命题，则p假且q假，m≥6，所以当命题“p或q”为真命题时，m＜6．

学生探索建构3：我想在第一位同学的解答中简化就可以，因为命题“p或q”为真命题，所以p和q中至少有一个是真命题，即-6＜m＜6或m＜5，解得m＜6．

说明：第一位同学的解题思路凸显了大部分学生的思路，即将问题分析清楚，分类讨论必须不重、不漏，进而达到目的；第二位同学思维敏捷，考虑到问题的分类比较烦琐，因此利用哲学思想“正难则反易”，从反面突破；第三位同学的认知水平要高于前两位，解决“或”命题何必一定要不重、不漏地分类呢？显然这位同学已经清晰地认知了问题，进而简化了分析和解答．

三、再上层楼，望尽天涯——思想方法视角讲评

讲评问题的最高境界在于引导学生从问题中管窥到思想方法的使用，我们知道数学思想才是高中数学最终给予学生教学最高端的层次，有了思想方法，学生解决问题不再拘泥于技巧，数学学习的眼界和问题解决的思考都能望尽天涯，再上层楼．

说明：通过简单的换元思想，结合数形结合思想，将问题转换为二次函数问题解决，对学生而言，这种问题的处理在于讲评时思想方法的渗透．

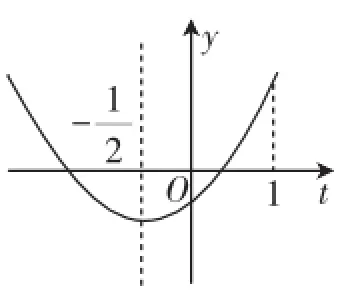
图2

说明：讲评此类含参数的三角、指数、对数等复杂方程解的问题，通常有两种处理思路：一是分离参数构建函数，将方程有解转化为求函数的值域；二是换元，将复杂方程转化为熟悉的二次方程，进而利用二次方程解的分布情况构建不等式或构造函数加以解决．本题正是以典型的问题引导学生对“有解”型问题的处理，增加其解决问题的经验．数学思想方法的学习和运用是一个潜移默化的过程，是在多次领悟、反复应用的基础上形成的．作为教师，应尽可能多地为学生创造条件让学生实践运用数学思想方法来解题，通过实践活动中主体（学生）对客体（问题）的认知结构不断的构建过程，促进学生数学思想的发展．试题讲评是很好的总结、回顾、强化，在运用数学思想方法上肯定能得到“升华”．

总之，试题讲评有了新时代的发展，不同于以往将问题随随便便解答即可的地步．本文从三个层面做了一定的阐述，限于水平有限，恳请读者提出批评指正，共同研究和深化．

1.朱永祥.再谈数学思想方法的挖掘和应用［J］.中学数学（上），2008（2）.

2.罗先礼.数学教学的实践与思考［J］.中小学数学（高中版），2008（12）.

3.展国培.有效教学，从关注学生开始［J］.中小学数学（高中），2013（1）.A