拥抱新年感恩良师*——编拟、赏析与年份相关试题

☉福建省厦门第一中学 王淼生

拥抱新年感恩良师*
——编拟、赏析与年份相关试题

☉福建省厦门第一中学 王淼生

寒暑交迭，万象更新.硕果累累的2014年悄然离去，满怀希望的2015年即将降临.为了感恩心中的良师益友——《中学数学》，作为贵刊忠实的读者、作者，想用自己独特的方式编拟四道与年份相关且集娱乐性、趣味性、知识性及数学文化于一体的不等式试题.让我们在品味数学的博大精深、感受数学的奥妙无穷、欣赏数学的和谐之美中拥抱新年！同时恭祝贵刊新年红红火火！万事如意！

一、编拟试题及解答

例1求满足以下条件时（x-2012）2+（y-2014）2的最小值：

（1）2016（x-1）2015+2014（x-1）2013+2012（x-1）2011+ 2010=0；

（2）2016（1-y）2015+2014（1-y）2013+2012（1-y）2011+ 2010=0.

解析：构造函数f（t）=2016t2015+2014t2013+2012t2011+ 2010.

由（1）、（2）便知f（x-1）=f（1-y），注意到函数f（t）为增函数，据此可得x-1=1-y⇒x+y=2.

由基本不等式a2+b2≥2ab的变式a2+b2≥可得

解析：无论是老教材还是新课标教材，无论是人教版还是其他版本教材，都有这样一道著名的例题，也就是我们常说的糖水不等式，即

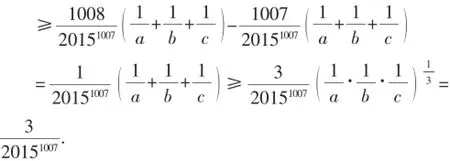
二、赏析试题及感悟

1.上述试题的渊源

客观地讲，上述四道试题难度较大，不亚于全国联赛试题，甚至与国际奥赛试题难度相当.咋一看无从入手！但从上述构思及解答过程不难发现：破解这些高难度不等式试题所采用的策略和工具都是些“草根”，如基本不等式、均值不等式、教科书例题等.这些试题不仅与年份相关，而且结构优雅、对称、和谐，让人在聆听新年钟声敲响之际，同时享受数学精神大餐，让人赏心悦目、心旷神怡.

其实这些试题并非空穴来风、从天而降，而是有源之水、有本之木.

尽管我国对构造法研究的时间不长，相应的构造法方面的论著也较少，但可喜的是近年来发展迅猛.新课标教材中明确涉及构造法，近年来的高考、竞赛中处处渗透构造法，尤其构造函数、图形（如文1、文2）已经成为中学数学中一道靓丽的风景线！构造法是一种神奇的解决问题的策略与方法.构造法没有固定的程序与套路，需要强烈的构造意识及厚实的基本功力，对培养学生思维的敏捷性、独特性及创造性有着不可替代的作用，常常让人豁然开朗、拍案叫绝.

例2的灵感来自著名的糖水不等式.糖水不等式是一个神奇的不等式，不论在不等式，还是在几何（如文3）、三角、函数等方面都有广泛应用.更为有趣的是糖水不等式在建筑设计、芭蕾舞造型、经济建设、军事斗争等方面发挥着越来越重要的作用.

基本不等式：a2+b2≥2ab的本源是在x2≥0中令x=a-b而得，因此我们还可以令，……得到一系列结论：……（如文4）.这些结论看似简单，甚至不屑一顾，其实功能强大！例3正是借助这些结论编拟而来.

2.一点感悟

上述四道试题的渊源说明不少试题是这样编拟命制出来的：依据教科书的定理、性质及结论的变形、引申，或源自教科书上的例题、习题的变式，类比归纳，或利用著名试题（如经典高考试题、全国联赛试题、国际奥林匹克试题等）进行改编、拓展.比如以下四道例题.

例6已知a＞1，b＞1，c＞1，求证：

1.王淼生.构造长方体巧证不等式［J］.数学通讯（教师刊），2012（5）.

2.王淼生.妙用三角形基本性质巧解竞赛试题［J］.中学数学（上），2013（3）.

3.王淼生.糖水不等式的精彩演绎［J］.中小学数学（高中版），2013（6）.

4.王淼生.数学美本质上终究是简单［J］.中学数学教学参考（上），2013（3）.

5.王淼生.追求简捷是数学教师永恒的主题［J］.中学数学月刊，2013（6）.

6.王淼生.运用均值不等式的灵魂在于凑配［J］.中学数学教学参考（上），2013（6）.

7.王淼生.例谈运用均值不等式的方法与策略［J］.数学通讯（教师刊），2013（2）.

8.王淼生.追寻数学问题2080的本来面目［J］.数学通报，2013（11）.

注：本文系全国教育科学规划教育部重点课题（立项批准号：GOA107017）“小学生数感的发展与特征研究及课程设计”；福建省“十二五”规划2013年度课题（立项批准号：FJJKXB13—083）“优化学生思维品质的魅力数学课堂模式研究”及厦门市2013年第三批课改课题（立项批准号：Z3042）“数学构造思想方法优化学生思维品质的实践研究”的阶段性成果.