基于有限元分析的高频轮轨力研究
王晶 陈建政

摘 要:测力轮对是目前最有效的轮轨力测量方法。根据国标要求,测力轮对最高测量频率为90Hz。由于在实际运行中,如果车轮受到与共振频率相同频率的激励时,很可能会产生模态共振,对轮轨力的测量产生很大的影响。文章采用频率为1-3000Hz的扫频激励对车轮进行谐响应分析。设计补偿滤波器,对固有频率处产生的共振峰值进行补偿。
关键词:高频轮轨力;模态;谐响应分析;滤波器
轮轨之间的作用力(简称轮轨力)是评判铁道车辆运行安全性和稳定性的重要参数。测力轮对作为目前测量轮轨力最直接最准确的方法。它的测量原理主要是以轮对作为轮轨力的检测传感器,通过测量车轮辐板有限点处的应变实现轮轨接触力的连续检测。能否精确地获取轮轨间的作用力直接影响着蠕滑、波磨及脱轨等的计算。
在实际的列车运行中,车轮所受的轮对力是一段从低频到高频的广谱。根据模态振动理论,当车轮在某些特定的频率处激励时,会引发模态共振。根据UIC518标准,测力轮对最高测量频率是90Hz,而根据文章仿真结果,轮对的一阶共振频率为159Hz,如果轨道激励中包含一阶或更高阶共振频率,则不可避免的将共振信号叠加到腹板应变上,造成很大的测量误差[1]。
对高频轮轨力的研究,首先对车轮有限元模型进行模态分析,然后对模型进行谐响应分析,求解出车轮应变响应。在应变响应中,各阶固有频率处会产生共振峰值,设计FIR数字滤波器,对频响曲线进行补偿滤波。
1 ANSYS有限元模型的建立及分析
在ansys中建立车轮三维模型,设置材料参数:杨氏模量E=2.1E11Pa,泊松比为0.3。单元类型的选择主要考虑结构的受力特性,选择的原则是对所选的单元可以使计算精度高、收敛速度快、计算量小模型网格划分采用的单元是六面体八节点实体单元Solid185,因为本论文分析的重点是轮辐处的应变,所以这一部分的单元划分密集一些,为了减少单元数,提高计算速度,对于其它部分的网格划分相对疏一些。在车轮内径施加全约束,防止车轮做平动和转动。建好的车轮有限元模型如图1所示。
图1 车轮有限元模型
2 模态计算及分析
模态分析用于确定车轮的振动特性,即结构的固有频率和振型。为获得车轮的固有属性,计算模态采用分块Lanczos法,提取车轮17阶模态,计算结果列于模态分析的基本思想是由于结构的模态密集而且相互耦合,应用物理分离模态技术难于获得模态参数,通过描述结构的动态性能矩阵方程解耦,从而可以使N 自由度的动力学特性用单自由度系统表示。其核心内容是确定用以描述结构系统特性的固有频率,阻尼比和振型等模态参数。计算模态分析从结构特性与材料特性等原始参数出发,采用有限元法形成系统的离散数学模型——质量矩阵和刚度矩阵,然后通过求解特征值的问题,确定系统的模态参数。由模态迭加法,可以分析结构在已知外载荷作用下的动态响应或稳定性问题。求解出车轮振型图提取前4阶如图2所示。
3 谐响应分析
任何作用在结构系统上持续的周期载荷都将在结构系统中产生持续的谐响应。谐响应分析是用于确定线性结构在承受随时间按简谐规律变化的载荷时稳态响应的技术,为了获得车轮在固有频率处实际的各类响应值,对模态分析后的车轮进行谐响应分析。
系统的动态特性可以用冲击响应函数h(t)来描述。t(h)的定义为任意时刻上系统对单位冲击输入的响应,则对任意输入x(t),系统的输出y(t)为
(3-1)
对上式两边去傅里叶变换,令X(?棕)是x(t)的傅里叶变换,Y(?棕)是响应输出y(t)的傅里叶变换,则可以得到响应函数的表达式为
(3-2)
式中, 为幅频特性;
为相频特性。
频率响应函数就是系统的幅频和相频特性。如果假定输入是频率为?棕的正弦波,输出也是一个相同频率的波。同一频率的输出振幅值比,等于系统的模|H(?棕)|;输出和输入的相位差等于系统的相角?准(?棕)[3]。
图3 应变频响曲线
若输入信号x(t)为单位阶跃信号,则进行傅里叶变化X(?棕)=1,H(?棕)=Y(?棕),则系统的输出响应的傅里叶变化即为系统的传递函数。文章设计的谐响应载荷输入为幅值恒定为1N,频率为1-3000Hz,经过计算求解出车轮应变的幅频和相频响应函数,由幅频响应曲线可知幅频响应中对应固有频率处会产生共振峰值。截取一段车轮上某个节点的应变频响曲线如图3所示。
4 FIR数字滤波器的设计
滤波器的作用是对输入信号起到滤波的作用。文章采用频率采样法设计FIR滤波器,滤掉共振频率下的共振峰值。
频率抽样法则是从频域出发,把给定的理想频率响应Hd(ej?棕)加以等间隔抽样得到Hd(k)即:
(4-1)
然后以此Hd(k)作为实际FIR滤波器的频率特性的抽样值H(k),即
(4-2)
根据Hd(k),由DFT定义可唯一确定有限长序列H(k),即:
(4-3)
根据采样定理,可以由频率响应函数在[0,2?仔]上的N点进行间隔采样利用这N个频域抽样值H(k),同样利用频率内插公式可得FIR滤波器的系统函数H(z),即:
图4 频率采样法设计流程
频率采样法内插公式: (4-4)
在抽样点之间存在一定的逼近误差。误差大小取决于理想频率响应的曲线形状,曲线变化越平缓,则内插值越接近理想值,逼近误差越小[4]。具体设计步骤流程如图4所示。
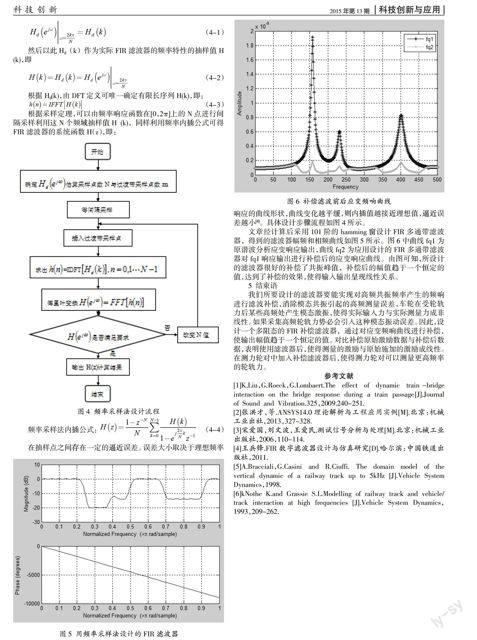
文章经计算后采用101阶的hamming窗设计FIR多通带滤波器,得到的滤波器幅频和相频曲线如图5所示。图6中曲线fq1为原谐波分析应变响应输出,曲线fq2为应用设计的FIR多通带滤波器对fq1响应输出进行补偿后的应变响应曲线。由图可知,所设计的滤波器很好的补偿了共振峰值,补偿后的幅值趋于一个恒定的值,达到了补偿的效果,使得输入输出呈现线性关系。
5 结束语
我们所要设计的滤波器要能实现对高频共振频率产生的频响进行滤波补偿,消除模态共振引起的高频测量误差,车轮在受轮轨力后某些高频处产生模态激振,使得实际输入力与实际测量力成非线性。如果采集高频轮轨力势必会引入这种模态振动误差。因此,设计一个多阻态的FIR补偿滤波器,通过对应变频响曲线进行补偿,使输出幅值趋于一个恒定的值。对比补偿原始激励数据与补偿后数据,表明使用滤波器后,使得测量的激励与原始施加的激励成线性。在测力轮对中加入补偿滤波器后,使得测力轮对可以测量更高频率的轮轨力。
参考文献
[1]K.Liu,G.Roeck,G.Lombaert.The effect of dynamic train-bridge interaction on the bridge response during a train passage[J].Journal of Sound and Vibration.325,2009.240-251.
[2]张洪才,等.ANSYS14.0理论解析与工程应用实例[M].北京:机械工业出社,2013,327-328.
[3]宋爱国,刘文波,王爱民.测试信号分析与处理[M].北京:机械工业出版社,2006,110-114.
[4]王兵锋.FIR数字滤波器设计与仿真研究[D].哈尔滨:中国铁道出版社,2011.
[5]A.Bracciali,G.Casini and R.Ciuffi. The domain model of the vertical dynamic of a railway track up to 5kHz[J].Vehicle System Dynamics,1998.
[6]kNothe K.and Grassie S.L.Modelling of railway track and vehicle/track interaction at high frequencies[J].Vehicle System Dynamics,1993,209-262.

