基于复杂网络的Braess悖论现象

刘 巍，曾庆山

（郑州大学 电气工程学院，河南 郑州450001）

0 引 言

Braess悖论是城市交通中一个看似矛盾的现象，其理论基础是博弈论中的纳什均衡［1］，即每个人的策略都是对其他参与人策略的最优反应。在交通网络中，由于每个人都不考虑自己的选择对其他出行者的影响，使得即使增加道路，交通延滞也不会减少，反而增加了出行者的出行时间。若增加道路后，城市交通系统总阻抗没有降低，则新增道路无意义。因此，在城市道路建设中应尽量避免Braess悖论现象的发生。

目前对于城市交通中的Braess悖论现象的研究大多局限于简单的交通网络模型［2－7］，而在复杂城市交通网络中，存在大量路段、交叉路口以及居民起讫点 （origin destination，O－D），不同起讫点间的居民有大量可选出行路径，且居民的出行行为互相影响。路段流量、阻抗随着居民出行行为的改变而变化，任一路段阻抗或起讫点间居民出行行为的改变均会对整个网络造成影响。本文根据城市交通网络的特点，应用复杂网络理论建立双层城市交通网络，并依据Braess悖论现象的成因对城市交通网络进行交通配流，同时分析路段实际通行能力、居民起讫点及新增道路对城市交通网络的影响，确定出造成Braess悖论现象的路段，给出改善城市交通的方案。

1 城市交通网络模型

本文基于复杂网络理论利用MATLAB建立一双层城市交通网络模型，下层网络为n×n网格的城市道路网络，上层为居民出行网络。

考虑到城市道路网络具有无标度性和流量集中性［8，9］，且居民往往集中在公园、商城、火车站等地，故居民出行网络采用无标度网络。

双层城市交通网络模型如图1所示。

图1 双层城市交通网络模型

虚线为城市道路网络，其为一5×5的网格，虚线为路段，两虚线交叉处为交叉路口。该网络具有25个交叉路口及40条道路。本文用G｛J，L｝表示城市道路网络，其中J为交叉口集合，L为路段集合。

双划线为居民出行网络，其为一含10个节点、15条边的无标度网络。每个节点的度至少为1，即至少有一个边经过该点，设定居民只能沿网格出行。为方便计算，居民出行点及目的地均设定在交叉路口处。用H｛B，E｝表示居民出行网络，其中B为O－D对端点的集合，E为任意O－D对间边的集合。为方便观察，设定在所研究时间段内所有O－D对间的流量均为1。

2 交通阻抗

交通阻抗是指交通网络上路段或路径之间的运行距离、时间、费用、舒适度，或这些因素的综合［10］。不同交通网络的阻抗随关注度不同而有所侧重。

交通阻抗包括路段阻抗和节点阻抗两部分。

2.1 路段阻抗

用路段走行时间表示路段阻抗，采用美国公路局开发的BPR函数，其形式为

式中：tij（0）——路段 （i，j）上的车辆平均自由走行时间，即路段上流量为零时车辆自由形式所需的时间；eij——路段 （i，j）的实际通行能力，即单位时间内可通过的最大车辆数；α、β为模型参数，一般的：α＝0.15、β＝4；Qij为路段 （i，j）上的车流量。

2.2 节点阻抗

节点阻抗为车辆在交叉路口花费的时间。城市交通网络中，由于交叉口多种多样，导致了其计算方法各异。

为方便计算，设定各个交叉路口的阻抗均相等，并将其阻抗计入到与之相连的路段上。

2.3 路径阻抗

O－D对间的路径阻抗即为连接O－D对的最短路径上的所有路段阻抗与节点阻抗之和。其可用图论中的经典算法Dijkstra算法求得。

在传统Dijkstra算法中，每次更新已识别点集都需要计算所有未识别点与起始点间的距离，随着城市道路网络网格数的增加，网络节点大幅增加，采用传统Dijkstra算法的运行时间也会大幅增加。考虑到城市交通网络中，绝大多数已识别点最多与3个未识别点直接相连，在路段阻抗差距不大时，搜索范围将在以起始点为中心的网格上逐步向外扩散，本文在原始Dijkstra算法的基础上新建一邻点表，该表中包含所有与已识别点直接相连的未识别点。新算法步骤如下：

（1）设初始节点为s，终止节点为m，J为网络所有节点的集合，P为网络已识别点的集合，U为网络中与任意已识别点直接相连的点的集合。对任意节点v∈J－P，D（v）为节点v到节点s的路径阻抗。

初始化：P＝ ｛s｝，U＝ ｛s1，s2…sn｝，s1，s2…sn为与节点s直接相连的点

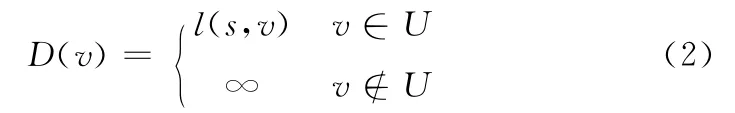
从集合U中寻找一节点w，其D（w）为最小，将节点w加入到集合P中，从集合U中删除节点w，并将w的所有不在集合U、P中的邻点加入到集合U中。D（w）计算规则如下

（3）判断节点m是否在集合P中，若在，结束运算，若不在，重复步骤 （2）。

表1为计算相同两点间阻抗时，不同算法的运行时间，可以看出，针对城市交通网络，改进Dijkstra算法运行速度有了明显提高。

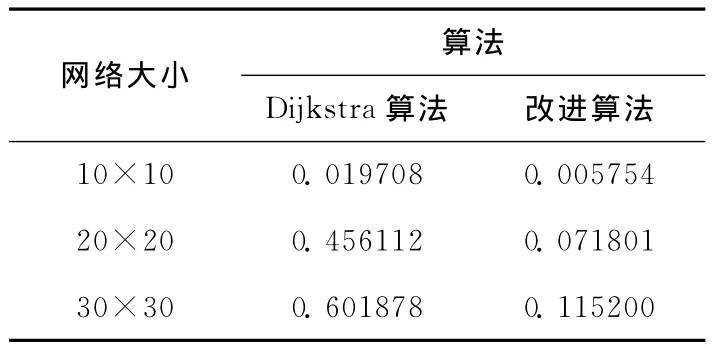
表1 两种算法的运算速度／s

2.4 网络总阻抗

交通网络的总阻抗为网络上的总行驶时间，可用下式计算

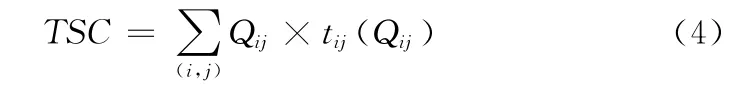
式中：TSC——网络总阻抗；Qij——路段 （i，j）上的流量；tij——路段 （i，j）上的阻抗函数。

网络总阻抗是判断交通网络是否出现Braess悖论现象的重要指标。

3 复杂交通网络上用户平衡配流

交通分配是指将交通需求按一定的择路原则分配到交通网络上，主要有两种分配模型［11］：用户平衡配流模型（UE配流模型）和系统最优配流模型 （SO配流模型）。

用户平衡配流模型中，每个人都力图使自己的出行时间最小，系统最优配流模型则力图使系统总出行时间最小。

因Braess悖论实质就是UE分配下的各个出行者间的不合作性，即每个人都力图使自己的出行时间最短，而不考虑自己的选择对他人的影响，故本文采用UE配流模型。

Wardrop平衡配流原则描述如下：在起止点间所有可供选择的路线中，使用者所利用的各条路线上的出行费用全都相等，而且不大于未利用路线上的出行费用。

1956年Beckmann等学者提出了满足Wardrop准则的数学规划模型，该模型如下

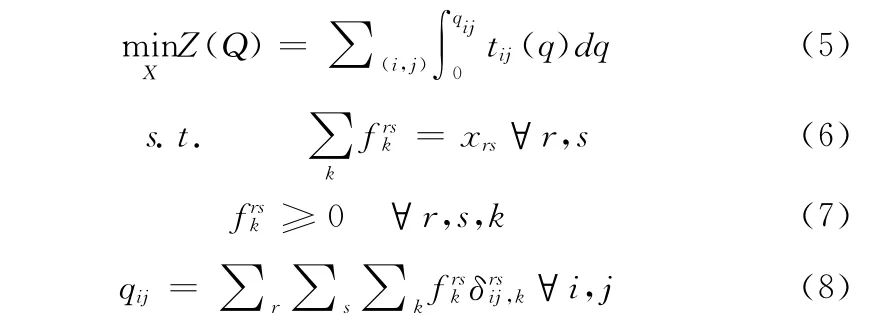
式中：tij——路段 （i，j）上的费用；qij——路段 （i，j）上的流量；frsk——O－D对r－s之间路径k 上的流量；xrs——所研究时间段O－D对r－s之间的交通需求量；为若路段 （i，j）在O－D对r－s之间的路径k上，其值为1，否则为0。

基于上述数学规划模型采用Frank－Wolfe方法利用MATLAB对双层城市网络进行用户平衡配流［12］，步骤如下：

（1）初始化，q0ij令路段流量q0ij＝0，采用BPR函数计算路段阻抗t0ij＝tij（q0ij），用 “全有全无”法将所有O－D对间的流量一次性加载到城市道路上，得到新的道路流量q1 ij，令迭代次数n＝1；

（2）更新路段阻抗，令tn ij＝tij（qn ij），对城市道路重新进行一次 “全有全无”交通流分配，得到一组附加流量pn ij；

（3）解方程

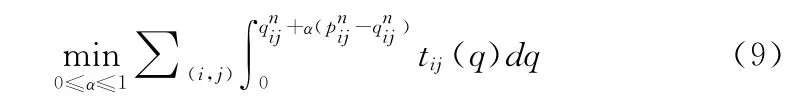
求得迭代步长αn，确定新的迭代点

（4）若满足

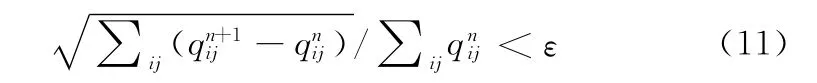
ε＞0为误差限值，则qn＋1 ij为平衡解，计算结束；否则，令n＝n＋1，返回步骤 （2）。

本文对图1所示双层城市交通网络进行用户平衡配流。

为方便观察，对所有路段 （i，j），令tij（0）＝1，eij＝5，对所有O－D对r－s，令xrs＝1。

进行用户平衡配流后的城市交通网络如图2所示。实线为道路流量网络，其中路段流量越大，线条越粗。系统总阻抗为40.2619。

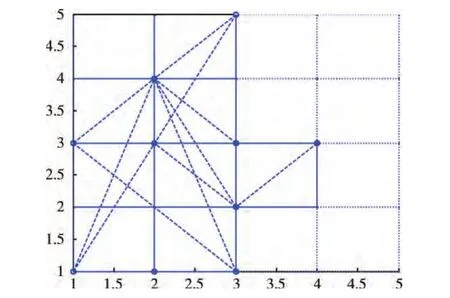
图2 进行用户均衡配流后的城市交通网络

本文采用G1（J1，L1）表示道路流量网络，道路流量网络为城市道路网络中删除流量为0的路段及节点后的网络。

4 复杂交通网络上的Braess悖论现象

通过查询城市道路网络中是否存在无意义的道路来判断城市交通网络中是否存在Braess悖论现象。

在对原始城市交通网络进行用户平衡配流后，依次查询流量大于0的路段对城市交通的影响，若删除该道路后，系统总阻抗并未增大，则该道路无意义。

在图2所示流量道路网络中，删除任一道路，系统总阻抗均会增加，即该城市交通网络并不存在Braess悖论现象。

分别讨论改变路段实际通行能力、新增居民起讫点或新增路段的情况下的Braess悖论现象。

4.1 改变路段实际通行能力

在城市交通网络中，经常需要通过拓宽城市道路以改善交通状况，本文研究城市交通网络中路段实际通行能力发生改变时的Braess悖论现象。

对所有流量大于0的路段 （i，j），依次令其道路通行能力eij＝10，即增强路段的通行能力。对图1所示城市交通网络重新进行用户平衡配流，计算系统总阻抗。

通过计算发现，存在5个方案，使得增强某路段通行能力后，系统总阻抗并未增加，其中，当增强点 （2，1）与 （2，2）间的路段通行能力时，系统总阻抗最高，为40.2768。

令点 （2，1）与 （2，2）间的路段通行能力e在区间［1，20］内变化，通过进一步的计算发现，当1≤e≤5或e≥6时，系统总阻抗随着e的增大而降低。其中当e＝6时，系统总阻抗为40.2789；当e＝12时，系统总阻抗降到40.2592，小于原系统阻抗40.2619，而后随着e的增大系统总阻抗基本保持不变。

由上述结果可以看出，在城市交通网络中，增强路段通行能力未必能够有效的缓解交通压力，有时甚至会增大系统总阻抗。在城市交通网络中，选择合适而非更大的路段通行能力能够更有效的改善城市交通。

4.2 新增居民起讫点

公园、居民区、医院、学校的建立会导致新的居民起讫点的出现，产生新的O－D对，使得城市交通网络发生改变。

在图1所示双层城市交通网络上，新增一居民出行点（2，2），并将该点以0.33的概率与其它居民出行点相连，生成一含11个节点，19条边的新的居民出行网络。

新的城市交通网络如图3所示，图中虚线为城市道路网络、实线为道路流量网络、双划线为居民出行网络。系统总阻抗为49.6153。

图3 增加居民出行点后的城市交通网络

将图3与图2对比，可以看出，新增居民出行点 （2，2）后，在用户平衡配流下，节点 （1，3）、（2，3）间的路段反而不再被使用。这是由于新的居民出行点的出现使得部分路段的阻抗增大，进而使部分O－D对之间的最短路径阻抗增大，该O－D对上的出行者将不再沿该路径出行，使得该路径上的路段流量受到影响，便出现了上述新的居民出行点的出现反而导致了原始路段不再被使用的现象。

若删除G1中的任意路段 （i，j）后，居民可沿城市道路网络G中的除 （i，j）外的路段出行，则无意义的路段数为6，即存在6个方案，使得删除城市交通网络中某一路段后，系统总阻抗并未增加。其中当删除点 （3，4）与（3，5）间的路段时，系统总阻抗最低，为49.5145，同时删除该路段后，部分流量将重新分配到节点 （1，3）、（2，3）间的路段上。

若删除G1中的任意路段 （i，j）后，居民仅能沿G1中剩余路段出行，则无意义的路段数为6。其中当删除点（3，3）与 （4，3）间 的 路 段 时，系统 总 阻 抗 最 低，为49.5313。

通过上述计算可知，新的居民出行点的出现可能会导致原本被使用的路段不再被使用，同时亦可能会引起Braess悖论现象的出现。

对某一存在Braess悖论现象的城市交通网络，相比于仅删除某个无意义的路段，在删除某个路段的同时合理增加部分原本看似无用的路段，可更加有效的降低系统总阻抗。

4.3 新增路段

为缓解交通压力，提高车速和通行能力，城市交通中往往会建立一些高架桥。

在点 （1，1）、（5，5）间建立一高架桥，构建图4所示城市交通网络。该网络中tij（0）＝1，eij＝5。

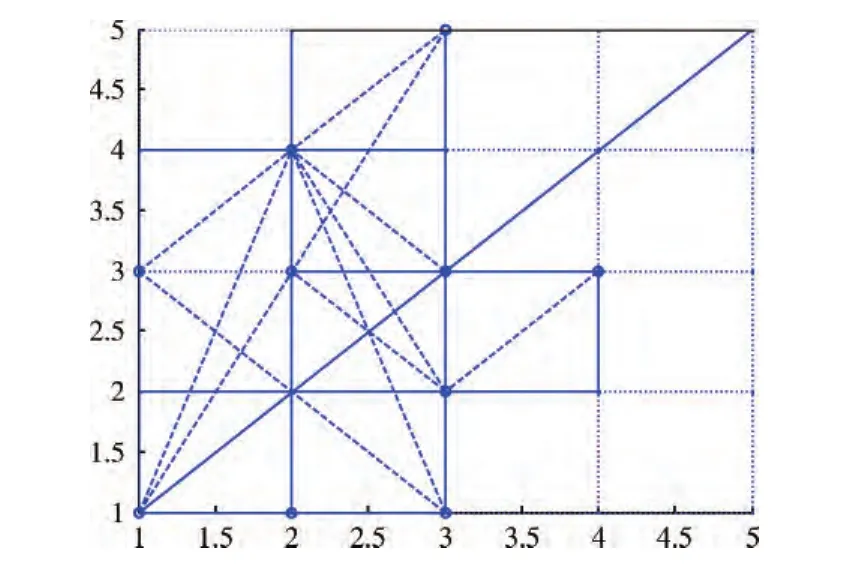
图4 建立高架桥后的城市道路网络

进行用户均衡配流后的道路流量网络如图，系统总阻抗为37.1696，小于原城市交通网络的系统总阻抗40.2619，系统性能有了较大提高。

由图4可以看出，该高架桥的建立导致了节点 （1，3）、（2，3）间的路段不再被使用，这是因为新的路段的出现使得部分O－D对间的居民沿新的最短路径出行，进而对其它O－D对间的居民出行路线产生影响，最终导致流量重新分配，使得任意O－D对间的最短路径都不再包括该路段。

通过计算发现，当删除点 （3，4）与 （3，5）间的路段后，用户平衡配流下的出行者将沿G1中剩余路段出行，系统总阻抗会降低，其值为37.1670。

通过建立高架桥，虽大幅降低了系统总阻抗，却也同时产生了Braess悖论现象，使得原来有意义的路段变得无意义，通过删除该路段可使系统总阻抗得到进一步降低。即建立新路段后合理删除部分原路段可使系统性能得到进一步的提高。

5 结束语

针对复杂城市交通网络中存在大量的路段及O－D对，使得通过传统方法研究复杂城市交通网络中的Braess悖论现象变得困难的情况，本文采用复杂网络理论，依据城市网络具有的无标度性和流量集中性，构建了一双层城市交通网络，其中上层为无标度居民出行网络，下层为城市道路网络。考虑到Braess悖论现象的实质便是博弈论中的纳什均衡，对城市交通网络进行用户平衡配流。在此基础上，研究复杂城市交通网络中的Braess悖论现象。

研究结果表明，在复杂城市交通网络中，相比于单纯的提高路段实际通行能力，选择合适的路段通行能力能更加有效的缓解交通压力。而改变居民起讫点及新增道路时，均可能造成Braess悖论现象的出现或消失。相比于仅通过拆除无意义道路或新建道路来改善城市交通，同时将两种方法配合使用，能取得更好的效果。本文在确定造成Braess悖论现象的路段同时，给出了改善网络状况的方案。本文采用方法及所得结果可为城市交通规划提供决策依据，具有一定的理论意义和实用价值。

［1］Macko M，Larson K，Steskal L’.Braess’s paradox for flows over time ［J］.Theory of Computing Systems，2013；53 （1）：86－106.

［2］Pala M，Baltazar S，Huant S，et al.Transport inefficiency in branched－out mesoscopic networks：An analog of the Braess paradox［J］.Physical Review Letters，2012，108 （7）：076802.

［3］ZHAO Chunxue，FU Baibai，WANG Tianming.Braess’paradox phenomenon of congested traffic networks ［J］.Journal of Transportation Systems Engineering and Information Technology，2012，12 （4）：155－160 （in Chinese）. ［赵春雪，傅白白，王天明.拥挤交通网络的Braess’s悖论现象 ［J］.交通运输系统工程与信息，2012，12 （4）：155－160.］

［4］Park K.Detecting Braess paradox based on stable dynamics in general congested transportation networks ［J］.Networks ＆Spatial Economics，2011，11 （2）：207－232.

［5］Lin Weihua，Hong K Lo.Investigating Braess’paradox with time－dependent queues ［J］.Transportation Science，2009，43（1）：117－126.

［6］Rapoport A，Kugler T，Dugar S，et al.Choice of routes in congested traffic networks：Experimental tests of the Braess paradox ［J］.Games ＆ Economic Behavior，2009，65 （2）：538－571.

［7］Askoura Y，Lebacque J，Haj－Salem H.Optimal sub－networks in traffic assignment problem and the Braess paradox ［J］.Computers ＆ Industrial Engineering，2011，61 （2）：382－390.

［8］WU Jianjun.Studies on the complexity of topology structure in the urban traffic network ［D］.Beijing：Beijing Jiaotong University，2008（in Chinese）.［吴建军.城市交通网络拓扑结构复杂性研究 ［D］.北京：北京交通大学，2008.］

［9］Jiang B.A topological pattern of urban street networks：Universality and peculiarity ［J］.Physica A，2007，384 （2）：647－655.

［10］ZHAO Yue.Study on the congestion characteristics and control methods on complex traffic network ［D］.Chengdu：Southwest Jiaotong University，2009 （in Chinese）. ［赵月.复杂交通网络拥堵特性及控制方法研究 ［D］.成都：西南交通大学，2009.］

［11］WU Jianjun，GAO Ziyou，SUN Huijun，et al.The complex of urban transport system ［M］.Beijing：Science Press，2011：36－40 （in Chinese）.［吴建军，高自友，孙会君，等.城市交通系统复杂性 ［M］.北京：科学出版社，2011：36－40.］

［12］ZHANG Hui.The analysis of the traffic flow distribution and failure of correlated traffic complex networks ［D］.Beijing：Beijing Jiaotong University，2012 （in Chinese）.［张辉.具有相关性的复杂交通网络流量分布及失效特性分析 ［D］.北京：北京交通大学，2012.］