技术创新网络的演化:杂交水稻育种技术案例①

宋天华，张庆普

(1.哈尔滨工业大学图书馆，哈尔滨 150090；2. 哈尔滨工业大学 经济与管理学院，哈尔滨 150090)



技术创新网络的演化:杂交水稻育种技术案例①

宋天华1，2，张庆普2

(1.哈尔滨工业大学图书馆，哈尔滨 150090；2. 哈尔滨工业大学 经济与管理学院，哈尔滨 150090)

研究了杂交水稻育种技术创新网络的演化规律，完成了对无标度网络度分布的精确数学推导。结果显示: 杂交水稻育种技术创新网络以S-曲线增长，遵循正态年龄分布修正的优先链接机制，是符合幂率分布的无标度网络。该研究结果补充和丰富了Barabsi无标度网络的增长机制和优先链接机制。相关创新组织和管理部门可以根据上述规律制定针对性的创新发展战略和创新指导政策，使创新组织获得领先技术创新优势，引领中国的创新行业抢占全球技术创新的制高点。

技术创新网络；专利引文网络；网络演化；杂交水稻育种技术

在经济发展中，技术创新扮演着最重要的角色。专利和专利引文是评价技术创新与扩散的两个有效指标，专利引文网络能很好地代表被授予专利的技术形成的创新网络[1,9]。一些学者基于美国专利和商标局专利数据研究了多技术领域[10,11]，探讨了全球技术创新网络的动态演化，一致认为网络遵循优先链接的概率模型。这意味着，新加入网络的专利创新倾向于链接那些有更多连接的专利创新，也倾向于链接年龄更大的专利创新。一些学者探讨了全球纳米技术领域的创新发展，认为专利引文网络很好地揭示了技术创新在国家、机构和技术主体中的扩散和发展[12]。Verspagen和Fontana等探讨了燃油电池的技术路径演化[13]。一些学者探讨了人造关节技术演化的连接性[14]、电处理聚合纳米混合物技术的演化[15]和核磁共振技术的演化[16]。这些学者从不同视角研究了技术创新的动态演化，认为技术创新的演化具有非线性、复杂性和累积生长性的特点，技术创新网络符合小世界网络的特点。

然而，以上研究没有深入揭示专利创新网络中创新节点年龄的影响。一些复杂网络研究[10，17-19]虽然证明了无标度网络优先链接的普遍存在性，但是其重要假设——网络以固定的速度增长——值得进一步探讨。此外，对技术创新网络的增长、拓扑特征、创新年龄影响及连接机制等进行整体而全面的研究是特别重要的——既能反映所研究技术领域的增长阶段、支配网络演化的重要创新和网络演化规律，还能丰富复杂网络理论的实证基础。但是，目前还没有对技术创新网络演化进行整体而全面的研究。

杂交水稻育种技术是一项先进的水稻育种技术。杂交水稻研究可追溯到20世纪。1964年，袁隆平首先在中国取得了研究突破，率先成功培育出成杂交水稻，从此打开了世界农业历史的新篇章。杂交水稻育种技术的主要目的是培育高产水稻。经过近50年的发展，大面积种植亩产900千克和亩产1 000千克的水稻的目标已在2011年和2014年实现[20-23]。中国的杂交水稻非常适合在许多国家种植。如果世界上杂交水稻累积种植面积达到7 500万公顷，那么，按每公顷增产2吨计算，将增加15 000万吨食物，能多养活4亿～5亿人口，能有效地保障世界食品安全[21]。因此，研究杂交水稻育种技术的创新演化具有特别重要的意义。

本文对杂交水稻育种技术创新网络的演化进行全面的实证研究和理论推导，既揭示了杂交水稻育种技术的演化，又丰富了技术创新理论和复杂网络理论。本研究集中于杂交水稻育种技术创新网络的更重要的性质——包括平均距离演化、聚类系数演化、增长规律、年龄链接模型和链接模型，基于技术创新网络的拓扑动力机制建立个体技术创新网络的演化模型，并应用平均场的理论方法精确计算个体技术创新网络演化模型的度分布方程。

1 研究数据和研究方法

1.1 数据处理

本文采用杂交水稻专利及其引文数据研究网络链接演化机制，所用数据为德温特创新系统的专利数据。获取数据的方法是: 以“hybrid rice”为检索词，选择主题途径作为检索项——包括专利题名和专利文摘，时间跨度是48年(1963—2010年)。最终共得到233件杂交水稻专利、51件后向专利引文、33件前向专利引文，所有这些专利及专利引文形成数据集。汇总这些数据后形成时间序列数据，对之进行清洗、整理和处理。

1.2 研究方法与模型

1.2.1 技术网络的重要属性特征与计算框架

(1) 度分布。将点i的度ki定义为连接到点i的其他点的数量。计算具有相同度数的点的数量产生度分布方程，表示为P(k)。不同类型的网络具有不同的度分布方程。

(2) 网络成长速度。定义每单位时间加入网络的新节点的数量为网络的成长速度。在通常情况下，用每年进入网络的新节点的数量作为网络的成长速度g，记gi=f(ti)。其中，ti是时间变量，gi是网络成长速度。

(3) 平均距离演化。平均距离是网络中任意两点间连接的边的平均数量，也叫平均最短路径。在技术创新网络中，一个更短的平均距离或最短路径意味着技术在网络中不同部分之间的扩散或传递更迅速。平均距离随时间的推移而不断变化，从而形成了平均距离的演化，记为DP(t)。平均距离的演化能指示出“网络距离”是怎样随时间推移而变化的。

(4) 聚类系数演化。聚类系数是一个测量网络聚类程度的重要指标。用Ci(Ci∈[0，1])表示点i的聚类系数，即点i与网络中其他点之间实际存在的边的数量与可能存在的边的数量之比。网络的平均聚类系数为1/N·∑Ci，即网络中全部节点聚类系数的平均值，反映了网络聚类的平均程度。这里聚类系数的演化是指网络平均聚类系数的演化，记为1/N·∑Ci(t)，表示网络的聚类程度或聚集程度随时间变化的变化。

1.2.2 技术创新网络链接核概率模型

复杂网络演化中最重要的是其链接机制。网络中的节点是如何链接的？网络是如何增长的？由前文研究可知，技术创新网络基本上都是无标度网络。由于无标度网络都遵守优先链接机制，因此本文假设新节点进入系统遵循优先链接机制，在优先链接机制下与系统内其他节点链接的概率∏(ki)与这些节点的度数ki相对应，节点的度越大则链接概率越大。复杂网络优先链接机制一般如方程(1):

(1)

同时，每个技术创新都有自己的生命周期，包括创新的产生、发展、成熟和衰落等阶段。在通常情况下，一个创新的专利引文(或其吸引力)会随着年龄Ai的增长而逐渐衰退。定义如下创新年龄吸引力的概率方程:

(2)

式(2)，f(Ai)是创新的专利引文(吸引力)的年龄变化分布，不同的技术创新网络可能存在差异。鉴于此，本文设计了技术创新网络中一个旧专利被进入网络的新专利引用的连接核概率方程，包含对应其度的优先链接和对应其年龄引文分布的连接概率。连接概率核方程如下:

(3)

式(3)中，β是一个调节参数。该核方程∏(k,A)决定了技术创新网络的链接演化。

2 个体技术创新网络演化机制与特征

用个体技术创新网络的度分布数据(网络的时间跨度为1963—2010年)拟合其最优曲线。专利引文网络的度分布和其拟合函数如图1所示。由图1可知，其数据趋势线在双对数坐标下近似是一条直线。其度分布趋势函数如下:

(4)

该分布是一个幂率分布。式(4)中:P(k)是度分布概率；k是节点的度；幂率指数γ为-2.01；α′是系统合成的常数，为81.12。该方程表明，杂交水稻技术创新网络是一个无标度网络。

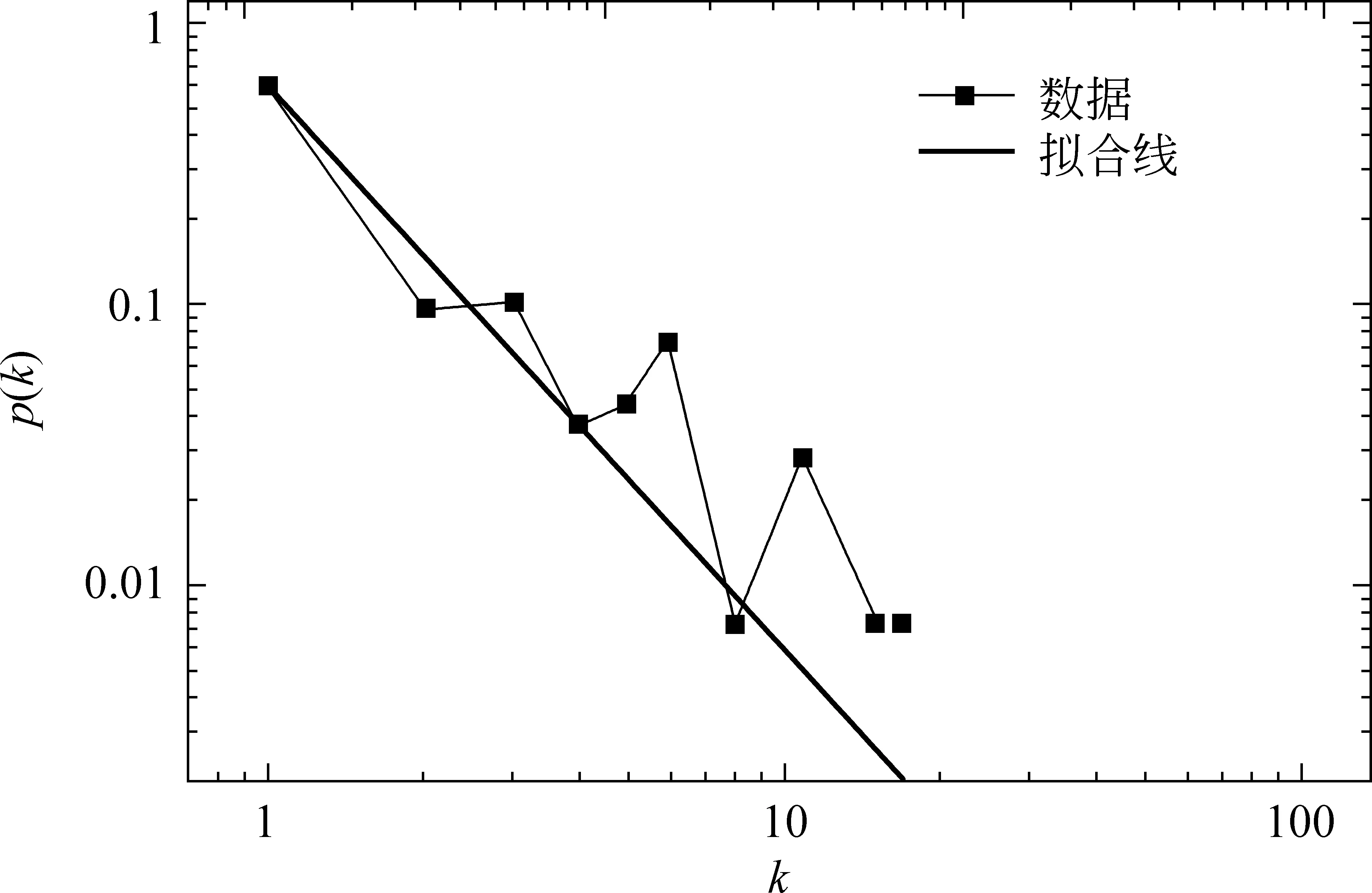
图1 杂交水稻技术创新网络的度分布

2.1 优先链接机制

无标度网络中的最重要机制是成长与优先链接，因此本文先检验其优先链接机制。由于一年的样本数据量太小，因此本文抽取1963—1994年的专利引文数作为度数k，抽取1995—2001年的专利引文数作为待分析的网络链接概率∏(ki)。为了减少该网络的数据波动，计算累积优先链接概率，定义为[24]

(5)

式(5)中，κ(k)为累积链接概率，结果见图2。从图2可看出: 虽然数据线显示出杂交水稻技术创新网络具有很好的优先链接性，但是它更接近一条曲线而非直线。这意味着: 如果只检验度，那么结果不是一个很好的线性优先链接。而符合幂率分布的优先链接应是线性优先链接，严格的无标度特征只能是线性优先链接的结果。在前文对度分布的拟合中，我们已得出该技术创新网络的度分布符合幂率分布。因此，除了节点度外，一定还有其他因素影响链接，否则不会出现这样的结果。前文设计的链接核包含年龄因素。如果年龄也是一个影响因素，那么我们推算，若检查某一段确定年龄专利引文的优先链接，则应能得到好的线性优先链接结果。

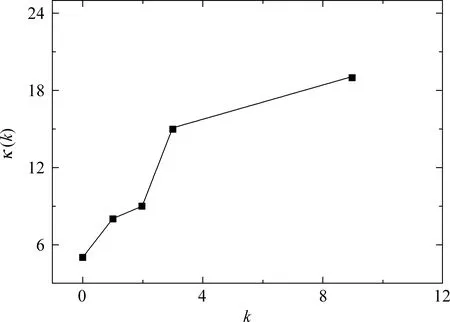
图2 基于度的杂交水稻技术创新网络优先链接

下面验证这一假设。抽取年龄为9～11岁的专利。专利年龄Agep的计算方法是: 以数据统计时间作为基准时间Yearbase，用基准时间减去专利许可时间(也即专利产生时间)Yearborn再加1，即

Agep=Yearbase-Yearborn+1

(6)

用9～11岁专利的引文数进行拟合，结果如图3所示，该年龄段的网络度分布基本符合线性优先链接。数据是累积优先链接的结果，对应的是累积年龄9～11岁专利的度k数据。这证实了被引专利的年龄对专利引文网络的链接具有重要影响。下一步将检验个体技术创新网络的年龄链接机制。

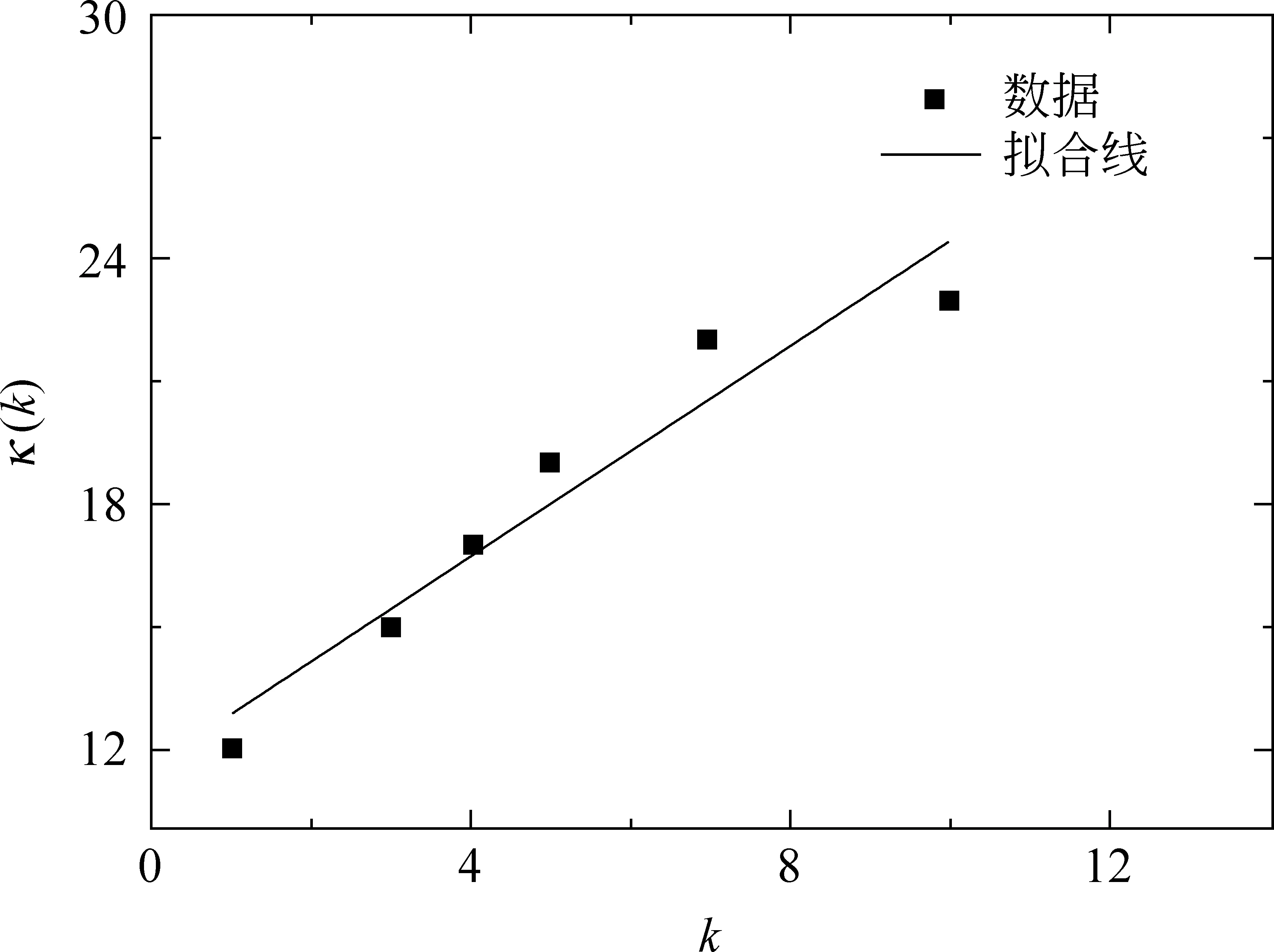
图3 年龄修正的杂交水稻技术创新网络的度优先链接

2.2 年龄链接机制

按照实证数据得到技术创新网络链接的年龄分布，见图4。图4中: 数据点为专利引文；横坐标是产生引用时的专利年龄A，纵坐标是专利引文数f(A)；带方块的实线是数据线，光滑的实线是拟合曲线。该拟合结果表明，技术创新网络年龄链接机制符合对数正态分布，该分布不同于以往文献中给出的年龄分布[10，13-16，24]。该方程表达形式如下:

(7)

式(7):A为被引专利的年龄；f(A)为年龄对应的专利引文数；y0为该网络中最初存在的引文数；Ac为峰值年龄点，在该年龄点之前的专利引文是不断增长的，在该年龄点之后的专利引文数量是不断地衰退的；D和w是两个系统参数。在该网络中，y0=-1.40，Ac=4.93，D=43.89，w=0.46。这表明: 在杂交水稻育种技术中，并非年龄最小的创新最有吸引力，年龄约为5岁的创新才最有吸引力。深层原因可能是: 在杂交水稻这个创新不太活跃的领域，创新被发现、被认识和被接受需要一定的过程和时间，这造成创新扩散与传播延迟。如何更早地认识创新的价值，认识并利用新出现的有价值的创新，缩短创新扩散与传播的时间延迟，提高创新及其扩散效率，是创新组织与管理机构应该思考的问题。

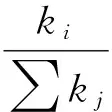
(8)

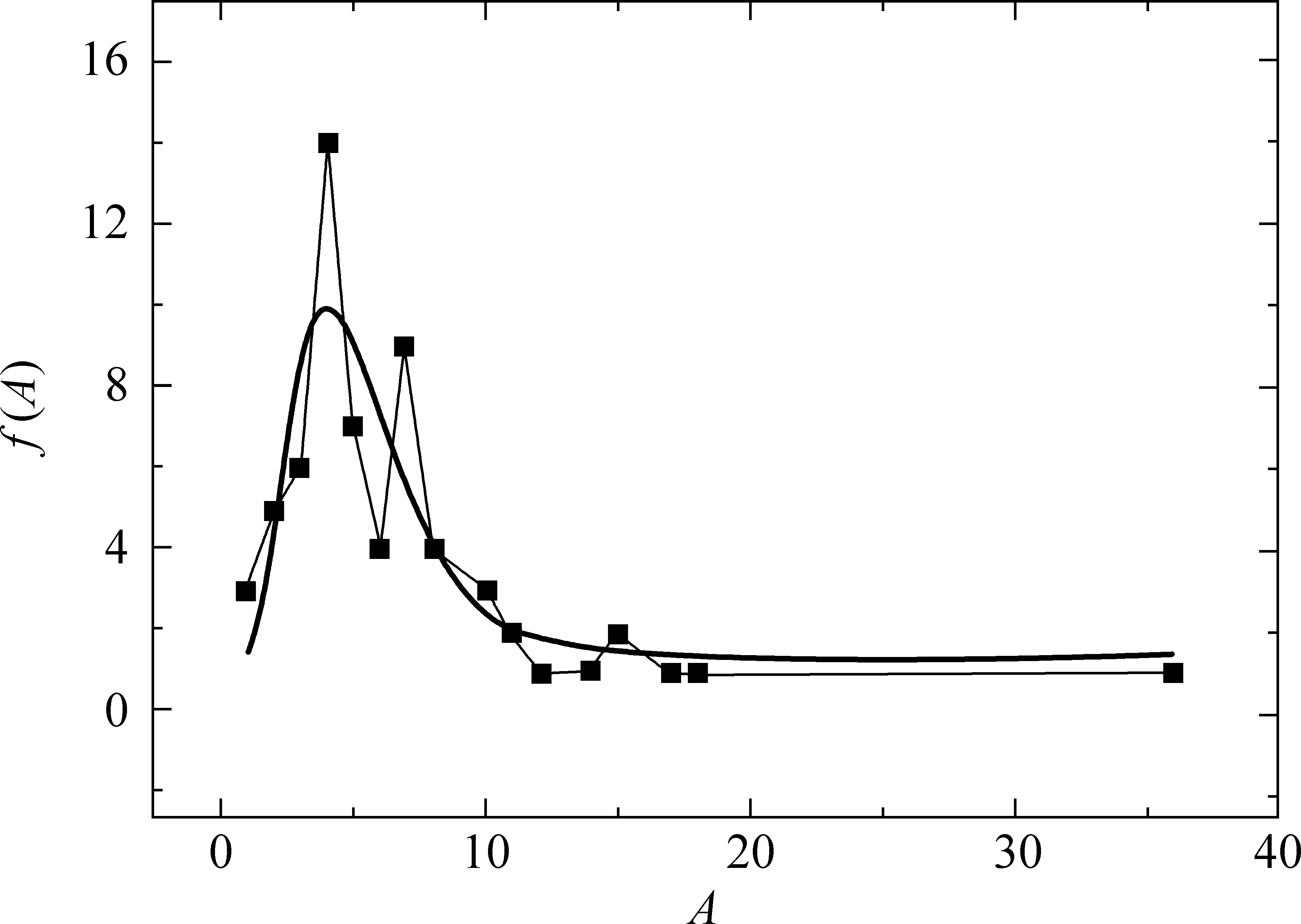
图4 杂交水稻技术创新网络链接的年龄分布

2.3 网络增长机制

无标度网络的重要演化机制是增长与链接，本节论述技术创新网络的增长机制。

许可专利进入专利数据库系统通常有时间延迟，如果将所有专利进入数据库系统的时间看作专利连接到网络的时间，那么系统时间延迟误差则会相互抵消。为了计算简化，本文将专利进入数据库系统的时间作为其连接到网络的时间。另外，专利引用也存在延迟，但该延迟可忽略。初步拟合杂交水稻技术创新网络的增长分布，如图5所示。由图5可知，多数数据点在图中直线分布两边，可看成一个线性分布。该分布方程如下:

(9)

式(9)中:ti是网络演化的第i时间步，因此ti值与i值是一样的；

a和b分别是曲线斜率和截距。该结果不同于多数文献设定的分布，多数文献认为随时间的推移网络的增长速度是固定不变的[10，23]。

图5 杂交水稻技术创新网络的增长速度

实际网络的增长分布起伏较大，虽然能得出大致的增长趋势，但是增长趋势曲线拟合得不好。为了更精确地计算网络增长的分布函数、降低系统噪声，本文计算了网络累积增长速度YG，其方程表达式如下:

(10)

式(10)中:g(ti)为技术创新网络的成长速度。

利用网络累积增长速度方程，可计算技术创新网络在29年期间的累积成长情况，结果如图6所示。杂交水稻技术创新网络的增长速度的最好拟合曲线是S-逻辑斯蒂曲线，其分布方程如下:

(11)

式(11)中:a是饱和期进入网络的节点的速度；b是决定曲线形状系统的参数；tc是反曲时间点，即增长速度最高的点，在该点前速度不断提高、在该点后速度不断下降、在饱和期速度达到最大。在该网络中，a=127.8，b=0.21，tc=15.03。这表明: 杂交水稻育种技术从1963年开始发展，到1982年出现第一个成熟创新，经历了约15年的不断加速增长进入快速发展期，随后进入高速发展期，目前其创新已逐渐接近成熟发展阶段。如果要取得更大进步，即进入新的创新成长周期，则需要获得突破性创新技术。

图6 杂交水稻技术创新网络的累积增长速度

2.4 平均距离与平均聚集系数的演化

杂交水稻技术创新网络的平均距离在整个网络成长的40年里保持在1.5左右(见图7)，基本上是不变的。这也说明该网络是“小世界网络”。

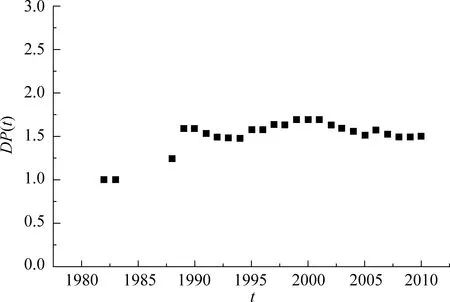
图7 杂交水稻技术创新网络平均距离的演化

在约40年里，杂交水稻个体技术创新网络的平均聚类系数近似向下线性下降(见图8)，这说明: 该网络的聚集性越来越低，同时该网络变得越来越均匀。随着网络的演化，支配网络成长的绝对重要技术越来越少，但是相对重要的技术越来越多，技术创新的发展越来越均衡。

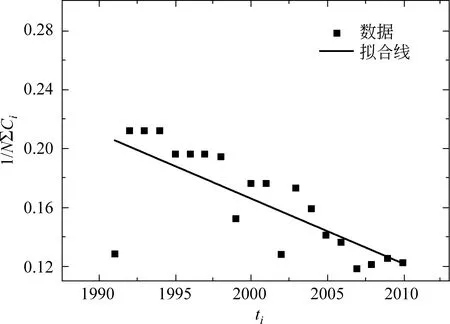
图8 杂交水稻个体技术创新网络平均聚类系数的演化

3 技术创新网络演化模型

3.1 技术创新网络动态建模

本文用前文获得的演化机制和演化规律构建个体技术创新网络的数量模型。重点强调的是: 构建该模型旨在获取影响该技术创新网络演化的主要机制，而非细化测量网络的每个数量细节。杂交水稻技术创新网络的特征不是独一无二的。尽管多数技术领域的创新网络因具有不同的生命周期而呈不同的年龄分布，但是大多数技术创新网络是优先链接机制与年龄分布共同作用的结果。另外，互联网也是一个复杂的演化网络，联系的增加和移出随着网页年龄的变化而不断变化，网络的拓扑性质很大程度上由这些动态性决定，因此其演化具有技术创新网络的一些特征。综上，下面设计的网络演化模型具有一定的普适性。

设: 在时间步t节点i的联系数为ki(t)；T(t)和N(t)是时间点的总数和联系的总数。设存在于系统中的所有点都是比较活跃的，它们能引起更多的创新。与图4一致，新节点是以下面函数的形式链接入网络的:

(12)

要强调的是，多数技术创新网络都有自己的增长模式，但是技术的生命周期规律决定了大多数技术创新网络的累积成长曲线都是S-曲线。

在t时刻，系统中每个点的平均联系数量〈k〉为

(13)

这样，我们可以系统地构建支配技术创新网络演化的动态模型，该模型包含支配技术创新网络演化的基本机制:

• 节点以S-曲线分布即方程(12)的分布方式加入网络；

• 将进入网络的节点遵循度数优先的原则与网络中的原有节点连接，优先链接分布方程为

(14)

其中m是网络初始状态下存在的联系数量；

• 将进入网络的节点按照网络中节点年龄的正态分布规律与网络中的原有节点连接，其分布函数为方程(7)；

• 综合链接分布模型∏(k,A)是度优先链接与节点年龄分布的核方程，其分布形式为方程(8)。

3.2 技术创新网络演化模型的度分布

本文基于前文构建的个体技术创新网络演化模型推算其度分布形式。文献[18]和文献[24]设计了利用连续理论计算一个技术创新网络的度分布的函数，该函数以个体节点的度和年龄为连续变量。在网络增长期，可近似地认定一个节点的度随着时间的推移按一定比率变化，是新增加联系的数量和其年龄分布之积所成的比率:

(15)

该方程的分母是在时间范围t下有向图中边的总数

(16)

那么，有

(17)

因为年龄链接f(A)是一个独立函数，因此先假设它是一个固定值。

由初始条件可知，每个节点在时刻ti有ki(ti)=m个联系，则有

(18)

更进一步，一个点有度ki(t)

(19)

这里，

(20)

一个节点在时间步ti进入系统的概率随时间的推移以S-曲线增长，即

(21)

(22)

对方程(22)求导，获得度分布P(k)，即

(23)

(24)

t→∞，则A→∞，有

(25)

设α=a·m·β·y0，则

(26)

方程(26)揭示了杂交水稻育种技术创新网络的度分布遵循典型的幂率分布，这与大量网络测量得到的分布形式非常一致。

4 结论

杂交水稻育种技术创新网络的度分布遵循典型的幂率分布，而网络增长符合S-曲线分布规律，目前该创新网络已接近技术成熟阶段。该网络的平均距离基本保持不变，网络随时间的推移变得越来越均匀、越来越不聚集——这是网络接近成熟阶段的特点。网络中的新节点也按网络中节点年龄正态分布与网络连接。年龄约为5岁的创新具有最大吸引力，因此相关创新组织应重视该年龄段的创新。

本文根据上述计算结果构建了技术创新网络演化整体模型，包括方程(12)、(14)、(7)和(8)。相关创新组织可以根据上述特点制定针对性的创新战略，以取得领先的创新优势。有关政策部门可以根据上述技术创新的特点制定相应的技术政策和创新政策，加速国家技术创新的步伐，加快推进相应创新行业步入新的创新周期，强占全球创新的制高点。

本文通过研究技术创新网络丰富和修正了无标度网络演化模型。本文的计算结果表明: 无标度网络的增长模式是多样的——不只是固定速度的增长，还包括S-曲线增长和指数增长等自然界和人类社会领域中各种增长模式。无标度网络的优先链接包含更多行为，特别是与网络节点年龄有直接关系。在真实世界中，只有在年龄修正的情况下，才能显示出明显的优先链接。最后，基于具体的增长模式和年龄修正的优先链接，本文精确地计算出杂交水稻育种技术创新网络遵循一个幂指数为-2的幂率分布。

[1] Meyer M S.Patent citation analysis in a novel field of technology: an exploration of nano-science and nano-technology[J].Scientometrics，2001(1): 163-183.

[2] Jaffe A B，Trajtenberg M.Patents，Citations & Innovations: A Window on the Knowledge Economy[M].MIT Press，2002.

[3] Murray F.Innovation as co-evolution of scientific and technological networks: exploring tissue engineering[J].Research Policy，2002(31): 1389-1403.

[4] Wartburg I V，Teichert T，Rost K.Inventive progress measured by multi-stage patent citation analysis[J].Research Policy，2005(34): 1591-1607.

[5] Park Y，Yoon B，Lee S.The idiosyncrasy and dynamism of technological innovation across industries: patent citation analysis[J].Technology in Society，2005(27): 471-485.

[6] Huang Z.Connecting NSF funding to patent innovation in nanotechnology(2001—2004)[J].Journal of Nanoparticle Research，2006(8): 859-879.

[7] Wong P K.Knowledge sources of innovation in a small open economy: the case of Singapore[J].Scientometrics，2007，70(2): 223-249.

[8] Silverberg G，Verspagen B.The size distribution of innovations revisited: an application of extreme value statistics to citation and value measures of patent significance[J].Journal of Econometrics，2007(139): 318-339.

[9] Wang J，Chang C -H，Lin S-W.Network structure of innovation: can brokerage or closure predict patent quality[J].Scientometrics，2010(84): 735-748.

[11] Valverde S，Solé R V，Bedau M A.Topology and evolution of technology innovation networks[J].Physical Review E，2007，56(118): 1-7.

[12] Li X，Lin Y L，Chen H C，et al.Worldwide nanotechnology development: a comparative study of USPTO，EPO，and JPO patents(1976—2004)[J].J. Nanopart Res.，2007(9): 977-1002.

[13] Verspagen B.Mapping technological trajectories as patent citation networks—a study on the history of fuel cell research[Z].Working Paper，2005.

[14] Davida B-T，Fernandoa J-S，Itziar C-M.Mapping the importance of the real world: the validity of connectivity analysis of patent citations networks[J].Research Policy，2011(40): 473-486.

[15] Lee P-C，Su H-N，Wu F-S.Quantitative mapping of patented technology-the case of electrical conducting polymer nanocomposite[J].Technological Forecasting & Social Change，2010(77): 466-478.

[16] Ribeiro L C，Ruiz R M，Motta E D.The diffusion of technological knowledge through interlaced networks[J].Computer Physics Communications，20110(182): 1875-1878.

[17] Jeong H，Néda Z，Barabsi A-L.Measuring preferential attachment for evolving networks[J].European Physics Letters，2003(61): 567.

[18] Youtie J，Iacopetta M，Graha S.Assessing the nature of nanotechnology: can we uncover an emerging general purpose technology?[J].J. Techno Transfer，2008(33): 315-329.

[20] 袁隆平.超级杂交水稻育种研究新进展[J].中国农村科技，2010(2/3): 24-25.

[21] 袁隆平.从育种角度展望我国水稻的增产潜力[J].杂交水稻，1996(4): 1-2.

[22] 刘春瑞.袁隆平的超级水稻突破亩产900公斤[EB/OL].(2011-09-20)[2012-04-15].http: //news.sina.com.cn/c/2011-09-20/040923182635.shtml.

[23] 成舸.超级稻大面积亩产首破千公斤[EB/OL].(2014-09-29)[2015-02-07].http: //news.sciencenet.cn/htmlnews/2014/9/304495.shtm.

Evolution of Technology Innovation Network: Case of Hybrid Rice Breeding Technology

Song Tianhua1，2，Zhang Qingpu2

(1. Library of Harbin Institute of Technology，150090 Harbin，China；2. School of Management，Harbin Institute of Technology，150001 Harbin，China)

This paper studies the evolution of innovation network for hybrid rice breeding technology，and calculates accurately the degree distribution of technological innovation network.The results show as follows: the growth of hybrid rice innovation network follows S-curve by time；the innovation network fits preferential attachment as amended aging Lognormal distribution，and the degree distribution of technology innovation network follows a power law distribution.These results adds and enriches the growth mechanism and preferential attachment of Barabsi’s scale-free network.Innovation organization and management departments could make directed innovation strategies and fitted managing policy based on the above regular，and make them gain the advantage of leading technology，and lead domestic innovation sections to hold a commanding point of technology innovation in globe.

technological innovation network；patent citation network；network evolution；hybrid rice breeding technology

受国家自然科学基金项目“基于引文网络图数据挖掘的热点技术领域预测研究”(71003020)、“开放式创新环境下装备制造企业知识吸收能力演化机理与提升路径研究”(71202159)的资助。

宋天华(1973— )，男，黑龙江人，哈尔滨工业大学经济与管理学院博士后，研究方向: 科学计量学、科技管理、技术创新。张庆普(1956— )，男，黑龙江人，哈尔滨工业大学经济与管理学院教授，博士生导师，研究方向: 知识管理、科技管理。

G353.12

A