含杂质的卢瑟福散射的蒙特卡罗模拟

李新霞，岳东宁，雷晓晨

(1.南华大学 核科学技术学院，湖南 衡阳 421001；2.中国科学院 等离子体物理研究所，安徽 合肥 230031)

含杂质的卢瑟福散射的蒙特卡罗模拟

李新霞1,2，岳东宁1，雷晓晨1

(1.南华大学 核科学技术学院，湖南 衡阳 421001；2.中国科学院 等离子体物理研究所，安徽 合肥 230031)

采用蒙特卡罗方法数值研究了杂质对α粒子卢瑟福散射的影响。杂质原子根据靶材的纯度以给定的概率随机替换靶材原晶格的原子。研究结果表明，考虑杂质后，出射粒子随散射角分布的曲线中形成了新的峰，峰的位置随杂质元素原子序数的增加向大角度方向移动；杂质的原子序数越低、含量越高，对卢瑟福散射出射粒子角分布的影响越明显；同时，入射粒子能量越低，杂质产生的峰对分布曲线的影响越明显。此外，对典型的C6+、N7+等重离子束的卢瑟福散射的模拟计算结果表明，重离子束对杂质有更好的分辨率。

卢瑟福散射；杂质；散射角；蒙特卡罗模拟

卢瑟福α粒子散射实验证实了原子的核式结构。在α粒子与靶原子的弹性散射过程中，由于库仑相互作用，α粒子的运动轨迹发生偏转，偏转角与靶材料原子序数及靶的晶体结构密切相关[1-3]。因此，理论上通过分析出射粒子在散射角方向的统计分布特征，可获得靶材的元素种类、材料的组分以及靶中杂质的含量等[2-5]。目前，卢瑟福散射技术被广泛应用于薄膜厚度测量、杂质成分及含量分析、化合物组分分析等核技术应用分析领域。

卢瑟福散射分析技术的关键是散射粒子的产额分析，它取决于具体的散射截面。对α粒子卢瑟福散射理论的研究表明，当碰撞参数b(入射粒子与靶原子核无相互作用情况下的最小直线距离)接近原子大小时，核外电子屏蔽效应导致小角度处的散射截面偏离卢瑟福散射公式[1]。刘宇等[2]通过计算机模拟散射过程证明在核力和核外电子屏蔽可忽略的合理能量范围内，靶原子间存在相互遮掩以及入射粒子发生多次散射是导致小角发散的原因。分析和测定材料组分是卢瑟福散射分析技术非常重要的应用。由于具有分析速度快、准确度高等优点，卢瑟福背散射(RBS)技术在国外已发展成为薄膜成分标准物质的定值方法[6-7]。刘运传等[8]利用RBS分析技术测定了第3代半导体材料AlxGa1-xN晶体薄膜中的铝含量,也获得了该晶体表面结构的信息。靶材样品均匀性的下降导致谱图分析过程复杂，即使采用RUMP、SIMNRA等专门的解谱软件，出现的多解现象最终降低了定量分析的精度。如何快速、准确地获得靶材的组分参数仍是卢瑟福散射分析技术研究的重点。

本文基于蒙特卡罗方法，运用计算机模拟研究杂质元素对卢瑟福散射实验中出射粒子在散射角方向的分布的影响。以散射实验中常用的金箔为例，杂质原子根据靶材的纯度以给定的概率随机替换金晶格的原子，具体计算几种典型的杂质，如Ag、Cu、Pb等的影响。此外，还研究杂质对C6+、N7+等重离子束卢瑟福散射实验的影响。

1 模型与理论分析

假定入射粒子与靶原子间相互作用过程为库仑力作用下的完全弹性碰撞，若同一时刻只考虑与单个靶原子的相互作用，出射粒子的散射角由库仑散射公式给出。

(1)

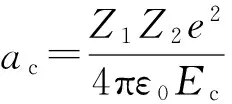
图1为1 MeV的α粒子沿极轴反方向轰击金原子靶发生卢瑟福α粒子散射的示意图，入射粒子数为2 000。

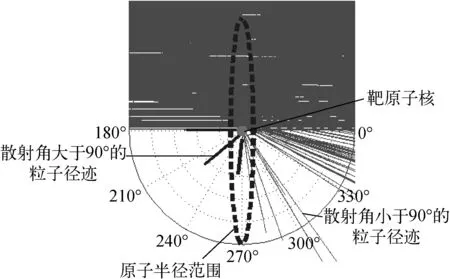
图1 卢瑟福α粒子散射示意图Fig.1 Schematic plot of Rutherford scattering experiment with Au target

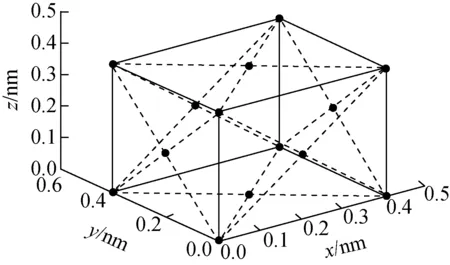
图2 金晶体结构示意图Fig.2 Schematic diagram of gold crystal structure

假设靶材为Au，其面心立方结构的点阵参数为a=b=c≈0.4 nm[9]。建立坐标系，选择晶面指数(001)，则垂直于晶面的法向量为(0,0,1)。晶面绕y轴旋转的角度记为β1(0<β1≤π/2),绕x轴旋转的角度记为β2(0<β2≤π/2)。选择β1=π/6，β2=π/3。金晶体结构如图2所示。

考虑杂质情况，假定杂质原子以某概率随机取代晶体中某位置的金原子，其中，概率由杂质的含量确定。本文根据金靶中常见杂质种类选择Ag和Cu。由于Ag和Cu与Au不在同一个元素周期内，因此对散射的影响更显著。

2 结果与讨论

选择薄靶并忽略原子间相互遮掩及多次散射的情况，首先模拟研究散射粒子在探测球面上的分布，如图3所示。入射粒子沿z轴负方向入射，粒子能量按平均能量Eave=1.5 MeV、σ=100 keV高斯分布随机选择，入射粒子数为5×105，探测球面的半径为3 m。由图3可知，绝大部分入射粒子只发生小角度的偏转，极少部分入射粒子发生大角度散射，这与卢瑟福散射实验的结论一致。

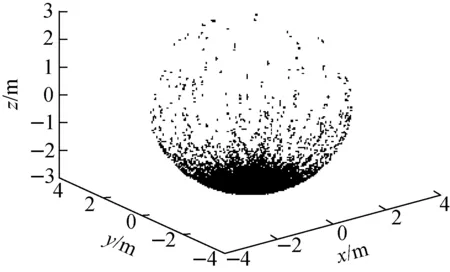
图3 散射粒子在探测球面上的分布Fig.3 Distribution of scattering particles in detection of spherical surface

对散射到以θ为中心角的微小角度内的粒子个数进行统计，并计算其在所有入射粒子中的归一化比例P(θ)，结果如图4所示。这里，考虑靶材为金晶体结构，即原子按面心立方结构排列。图中分别给出了入射粒子平均能量为1.2、1.5、2.0、2.4 MeV时P(θ)随θ的分布，随着入射粒子平均能量的增加，P(θ)的峰值向小角度方向移动，且峰值增大。这个现象与式(1)的结论一致：碰撞参数b不变，当Ec增大时，θc减少。因此，实验时，为获得较好的产额分析，入射粒子的能量不宜太高。

图4 散射粒子角分布Fig.4 Angular distribution of scattering particles

图5分别示出了Ag和Cu杂质浓度不同时散射粒子的角分布。引入杂质后，散射粒子的角分布出现了明显的第二峰，同时，新的峰随原子序数的增加向大角度方向移动，这表明杂质元素的原子序数越低，入射粒子发生小角散射的概率越高。表1列出了不同浓度的杂质Ag和Cu对散射粒子角分布峰值PM的影响。在本次模拟参数下，杂质Ag的含量每增加1%，对应PM降低约0.020%；杂质Cu的含量每增加1%，对应PM降低约0.034 4%。Ag相对于Cu，由于其原子序数更接近于Au，使得Ag对PM的贡献更大。

图5 Eave=1.5 MeV时杂质Ag和Cu对散射粒子角分布的影响Fig.5 Effect of impurities Ag and Cu on angular distribution of scattering particles with Eave of 1.5 MeV

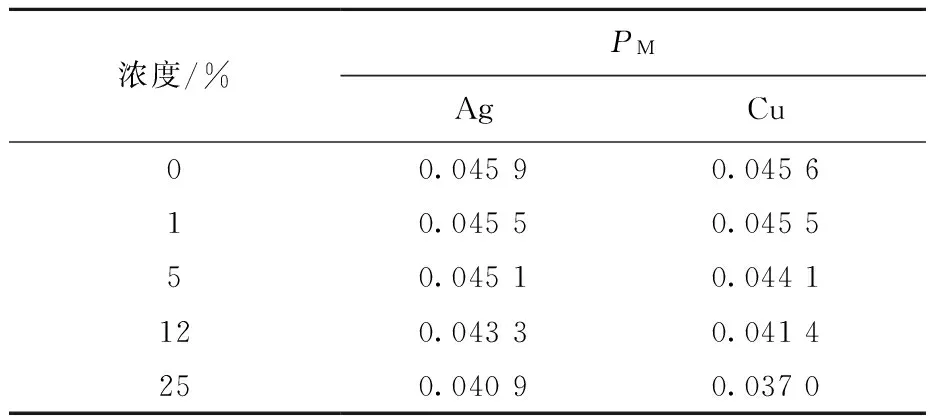
表1 Eave=1.5 MeV时不同浓度杂质Ag和Cu对PM的影响Table 1 Effect of impurities Ag and Cu on PM with Eave of 1.5 MeV

图6、7分别示出了入射粒子能量为0.9和2.4 MeV时，杂质Ag和Cu对散射粒子角分布的影响。这里，计算靶纯度为100%、99%、95%、88%、75%(对应的杂质含量为0%、1%、5%、12%、25%)的5组参数。经比较不同入射粒子能量下杂质对角分布的影响可知，入射粒子束的平均能量越低，P(θ)随散射角θ的变化曲线越平滑，杂质对大角散射的影响越明显，PM越小；平均能量越高，PM对应的θ越小，杂质对大角散射的影响越小，PM越大。在图中，P(θ)在θ很小时近似为0，这是由于在实验上正入射时粒子发生了强烈的背散射现象。计算不同平均能量对应不同的临界角θS，出射粒子的散射角θ>θS，θS由靶材料中原子序数较低的元素决定。表2列出了不同能量下Ag和Cu对应的临界角θS。

图8示出了在入射粒子束平均能量Eave=2.0 MeV时，入射粒子分别为He2+、C6+、N7+情况下，杂质Ag对P(θ)分布的影响。其他计算参数与图6相同。相比而言，C6+、N7+对杂质粒子有更好的分辨率，P(θ)的峰值向大角度方向移动，更利于实验的统计分析。同时，卢瑟福微分散射截面σc∝(Z1/E)2，入射粒子质量基本不影响卢瑟福散射角分布。

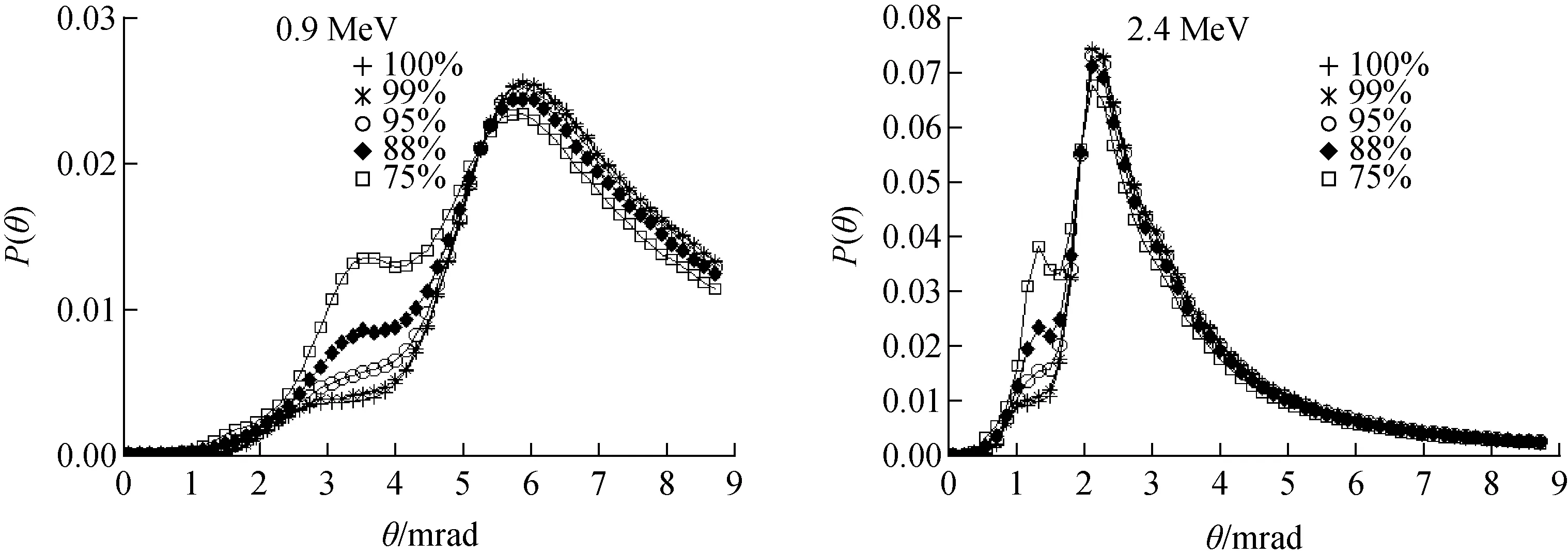
图6 Eave=0.9 MeV和2.4 MeV时含杂质Ag的出射粒子角分布Fig.6 Angular distribution of scattering particles with presence of impurity Ag under Eave=0.9 MeV and 2.4 MeV

图7 Eave=0.9 MeV和2.4 MeV时含杂质Cu的出射粒子角分布Fig.7 Angular distribution of scattering particles with presence of impurity Cu under Eave=0.9 MeV and 2.4 MeV

图8 He2+、C6+、N7+入射时含杂质Ag的出射粒子角分布Fig.8 Angular distribution of scattering particles with presence of impurity Ag for He2+, C6+ and N7+

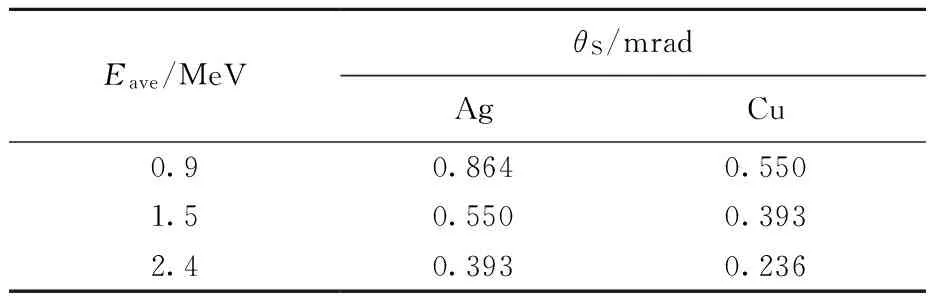
表2 不同能量下Ag和Cu对应的临界角θSTable 2 Critical angle θS for Ag and Cu under different injected energy

3 小结

本文采用计算机模拟研究了杂质对卢瑟福散射的影响。根据金靶的纯度引入杂质随机替换原来面心立方点阵结构中的金原子。研究结果表明：杂质导致了出射粒子角分布P(θ)形成新的峰，该峰的位置随杂质元素原子序数的增加而向大角度方向移动；同时，杂质的原子序数越低，含量越高，PM下降越快；出射粒子的散射临界角θS由靶材中原子序数较低的元素决定；不同粒子束平均能量下，随着能量的降低，杂质对角分布的影响更明显。此外，典型的C6+、N7+等重离子束散射分析模拟结果表明，采用重离子束能获得更好的分辨率。本文的研究将为与卢瑟福散射相关的核技术分析中实验数据的处理以及快速、准确测定杂质的种类和含量等提供参考。

[1] 杨福家. 原子物理学[M]. 北京：高等教育出版社，2008.

[2] 刘宇,唐昌建. 卢瑟福散射及其计算机模拟[J]. 原子能科学技术，2010，44(11):1 281-1 286.

LIU Yu, TANG Changjian. Rutherford scattering and its computer simulation[J]. Atomic Energy Science and Technology, 2010, 44(11): 1 281-1 286(in Chinese).

[3] 赵国庆. 卢瑟福背散射分析[J]. 理化检验:物理分册,2002，38(1):41-46.

ZHAO Guoqing. Rutherford backscattering analysis[J]. Physical Testing and Chemical Analysis: Physical Testing, 2002, 38(1): 41-46(in Chinese).

[4] MORGAN D V. Thin-film analysis using Rutherford scattering[J]. J Phys D: Appl Phys, 1974, 7: 653-662.

[5] 刘超卓. 分析薄膜厚度与成分的卢瑟福背散射技术[J]. 理化检验:物理分册，2010，46(7):436-440.

LIU Chaozhuo. Rutherford backscattering technique for analysing the thickness and composition of thin films[J]. Physical Testing and Chemical Analysis: Physical Testing, 2010, 46(7): 436-440(in Chinese).

[6] WU M F, VANTOMME A, HOGG S. Rutherford backscattering/channeling study of a thin AlGaN layer on Al2O3(0 0 0 1)[J]. Nucl Instrum Methods Phys Res B, 2001, 174(1): 181-186.

[7] ECKSTEIN W, MAYER M. Rutherford backscattering from layered structures beyond the single scattering model[J]. Nucl Instrum Methods Phys Res B, 1999, 153: 337-344.

[8] 刘运传,周燕萍,王雪蓉,等. AlxGa1-xN晶体薄膜中铝含量的卢瑟福背散射精确测定[J]. 物理学报，2013，62(16)：162901-1-162901-5.

LIU Yunchuan, ZHOU Yanping, WANG Xue-rong, et al. Accurate Rutherford backscattering spectroscopy measurement of aluminium composition in AlxGa1-xN crystal film[J]. Acta Physica Sinica, 2013, 62(16): 162901-1-162901-5(in Chinese).

[9] 刘培生. 晶体点缺陷基础[M]. 北京：科学出版社，2010.

Monte Carlo Simulation of Rutherford Scattering with Presence of Impurity

LI Xin-xia1,2, YUE Dong-ning1, LEI Xiao-chen1

(1.SchoolofNuclearScienceandTechnology,UniversityofSouthChina,Hengyang421001,China;2.InstituteofPlasmaPhysics,ChineseAcademyofSciences,Hefei230031,China)

The effect of impurities on the Rutherford scattering experiment was analyzed numerically based on the Monte Carlo method. The positions of target atoms in the crystal lattices were replaced by impurity’s atoms and it is proportional to the purity quotient of target. Taking into account the effect of impurity, the results show that the presence of impurity leads to a new peak in the angular distribution of the outgoing particle and the location of this new peak moves to the larger angle with increasing atomic number. Meanwhile, the lower the atomic number and the higher the content of the impurity element are, the more contribution to the formation of newly angular distribution peak is. At the same time, lower average energy of incident particles results in significant effect of the impurity. In addition, the analysis results of the typical heavy ion beam of C6+and N7+on the Rutherford scattering experiment with the presence of impurities indicate that improved distinguishability could be obtained comparing with the α particle.

Rutherford scattering; impurity; scattering angle; Monte Carlo simulation

2014-06-16;

2014-09-03

国家自然科学基金资助项目(11347002)；湖南省教育厅优秀青年基金资助项目(12B107)

李新霞(1973—)，男，湖南湘潭人，副教授，博士，从事核技术及应用研究

O571

A

1000-6931(2015)10-1740-05

10.7538/yzk.2015.49.10.1740