离心式上充泵首级叶轮空化特性与试验研究
朱荣生,蒋旭松,付 强,龙 云,王秀礼,习 毅
(江苏大学 流体机械工程技术研究中心,江苏 镇江 212013)
离心式上充泵首级叶轮空化特性与试验研究
朱荣生,蒋旭松,付 强,龙 云,王秀礼,习 毅
(江苏大学 流体机械工程技术研究中心,江苏 镇江 212013)
为研究和改善核电站离心式上充泵首级叶轮空化性能,采用数值模拟方法进行优化分析。将叶片数改为4片,研究了泵的最佳空化性能、扬程和效率。结果表明,最大流量工况点扬程模拟值与试验值的相对误差为2.9%,空化余量相对误差为3.6%,试验结果和模拟结果相吻合。将空化细分为初生空化、发展空化、临界空化、严重空化和断裂空化5个阶段,分析表明:初生空化时汽泡首先出现在叶片进口背面处,临界空化状态以后叶片工作面也开始出现汽泡;在发展空化到严重空化状态之间,空化和叶轮蜗壳动静干涉共同影响叶轮内的压力脉动规律;严重空化状态之后,空化成为主要影响因素,压力脉动变得相对稳定,叶轮进口和中部的压力脉动幅值明显减小,但叶轮出口处仍然保持较高幅值且比较规律的压力脉动。
上充泵;首级叶轮;空化;压力脉动;数值模拟
离心式上充泵是核电站一回路化学和容积控制系统的重要组成部分,也是难度仅次于主泵的核安全Ⅱ级设备[1]。上充泵具有流量小、高扬程、高转速、功率大的特点,属于低比转速泵。
国内外不少学者对上充泵进行了研究。文献[2]简要分析了上充泵主轴断裂事故的原因;王延合等[3]介绍了300 MW离心式上充泵技术要求、结构特点和材料选用;付强等[4]对1 000 MW级离心式上充泵的转子轴系进行了扭振计算。
空化(又称汽蚀)会导致泵性能下降,损坏过流部件并产生振动和噪声。Couiter-Delgosha等[5]结合CFD技术和试验对离心泵汽蚀进行了研究;王维军等[6]提出了离心泵空化初生判定准则,并给出了一种空化分类;张德胜等[7]通过建立的瞬态数学模型对特种涡轮驱动混流泵的瞬态空化特性进行了分析;刘厚林等[8]采用3种不同的空化模型对离心泵空化进行了数值计算;王松林等[9]对比分析了离心泵叶轮在空化和非空化状态下内部的压力脉动特性。
本文对上充泵首级叶轮叶片数进行优化,将模拟和试验结果进行对比,对上充泵首级叶轮的空化特性进行详细分析。
1 计算模型及设置
1.1 样机参数和结构
离心式上充泵为多级泵,空化发生在首级叶轮处。为研究上充泵首级叶轮空化特性,专门设计了上充泵首级样机,采用环形吸水室结构,压水室使用双蜗壳,初始叶片数为3,其结构示意图如图1所示。叶轮进口直径为140 mm,出口宽度为12 mm。首级叶轮上充工况点流量Q=34 m3/h[1],转速n=4 500 r/min,最大流量工况点Q=160 m3/h,必需空化余量(NPSHR)≤7.8 m。
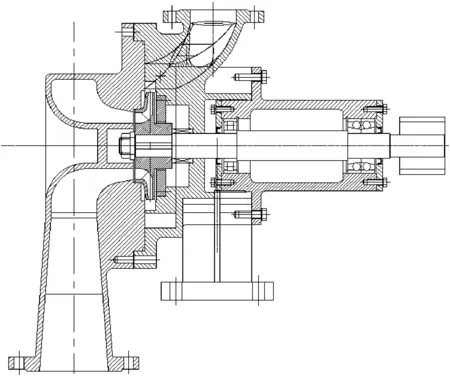
图1 首级样机结构Fig.1 Structure of the first prototype
1.2 三维建模和网格划分
采用Pro/E对上充泵首级模型进行建模,选用ANSYS ICEM和四面体非结构化网格对模型进行网格划分,并对局部区域加密。其中,环形吸入室网格数为431 856,叶轮网格数为703 867,蜗壳网格数为568 329。经过无关性检查表明网格满足计算要求。网格划分如图2所示。
图2 网格划分Fig.2 Grid division
1.3 计算设置
整个流体计算域采用SSTk-ω湍流模型;使用Zwart-Gerber-Belamri空化模型[8]描述汽泡生成和溃灭;使用压力进口、流量出口作为边界条件;水的饱和蒸汽压为3 170 Pa,汽泡平均直径设为2×10-6m,进口处水的体积分数设为1,汽泡的体积分数设为0。
2 叶片数优化设计
叶片数过多会增加进口排挤,降低叶片空化性能。因此,文献[1-4]中上充泵首级叶轮统一采用3叶片数的方案。但增加叶片数可增加叶片表面受力面积,减小工作面和背面压差,这有利于提高空化性能。因此,本文对3叶片数方案进行改进,设计了叶片数Z=3、4、5、6、7,共5种方案。
最大流量工况点下不同叶片数时的扬程H、效率η和NPSHR列于表1。由表1可见,随着叶片数增加,扬程逐渐增加,其中3叶片数方案的扬程比4叶片数方案低了11.5%,差别较大,Z=4、5、6、7叶片数方案扬程相差不大。3叶片数方案的效率比4叶片数方案低了10.3%,Z=4、5、6、7叶片数方案的效率相差很小。随着叶片数的增加,空化性能呈现先变好后变差的趋势。4叶片数方案的空化性能最好,3、4、5叶片数方案的空化性能相差不大。叶片数较少时,工作面和背面压差是影响空化性能的主要因素,从5叶片数开始,叶片进口排挤成为控制空化性能的主要因素,使得空化性能越来越差。综合水力性能和空化性能的对比,结合实际铸造加工等因素的影响,选择4叶片数叶轮为最优方案。
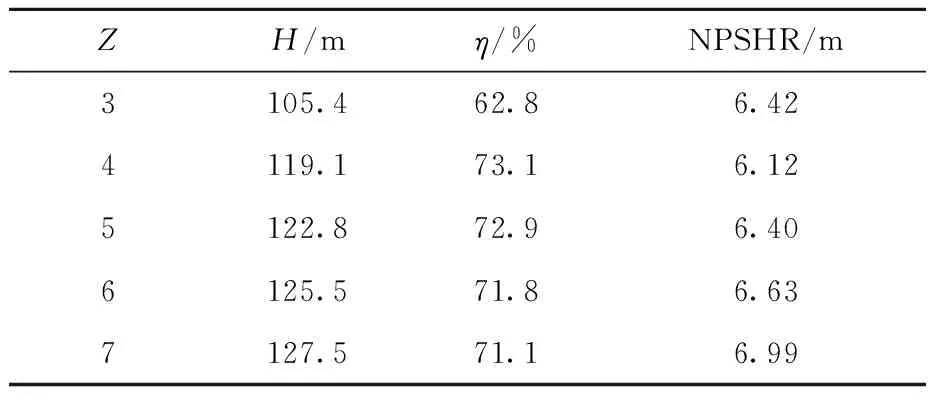
表1 泵性能参数Table 1 Pump performance parameters
3 空化试验
3.1 空化试验台
空化试验方法很多,在开式试验台上做空化试验是最常用的方法之一。采用开式试验台做空化试验操作简单、安装快捷、试验成本低,但如果设备选择不合理,安装操作不当,会严重影响试验精度。为保证进口密封性,在进口阀门处采取水封措施。空化试验时,测定空化余量的方法是关小进口阀门,增加进口阻力,逐渐降低泵吸入口压力,直到泵扬程下降3%。图3示出空化试验台原理图。图4示出首级叶轮水体图和实物图。
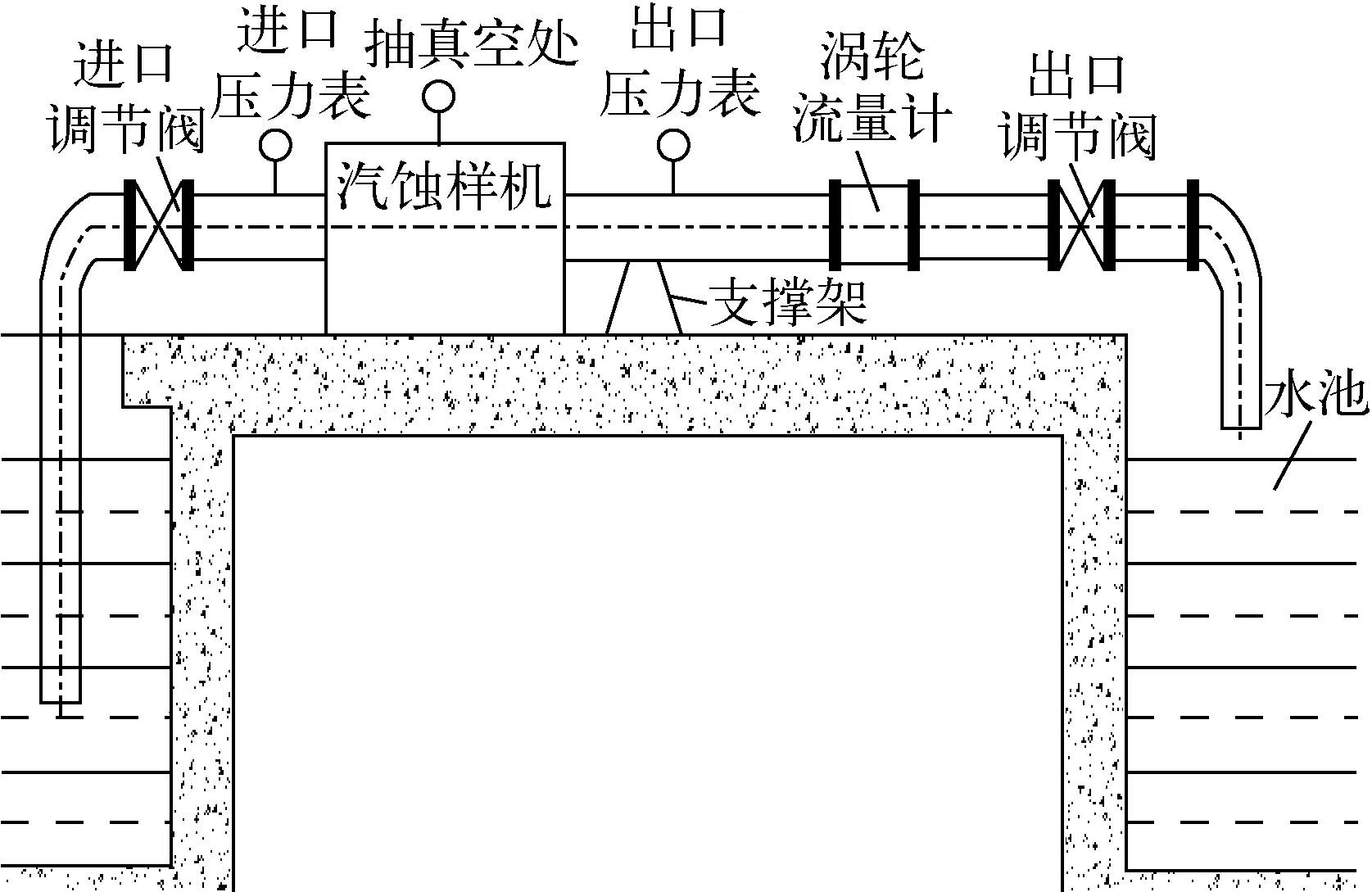
图3 空化试验台原理图Fig.3 Schematic of cavitation test device

图4 首级叶轮水体图和实物图Fig.4 Water body and material of the first stage impeller
3.2 试验结果及分析
水力性能模拟与试验结果如图5所示。由图5可见,上充工况点的扬程模拟值为157.6 m,试验值为149.9 m,两者相对误差为5.1%。最大流量工况点的扬程模拟值为119.1 m,试验值为115.7 m,两者相对误差为2.9%。最高效率在流量为140 m3/h附近,其模拟值为75.2%,试验值为73.3%,两者相对误差为1.9%。综合数值计算和试验结果可看出,从零流量点到大流量点,模拟值和试验值逐渐接近,最高效率点往大流量点偏移,这是因为设计时为了保证最大流量工况点的空化性能,偏向大流量点设计的缘故。上充泵首级叶轮首先要保证空化性能,其次才要兼顾水力性能,上充泵的水力性能主要由后11级叶轮保证,因此这种偏差是合理的。
要想真正理解这首词,首先得思考两个问题。一是作者为什么要写这首词?二是作者想要通过这首词来表达什么?首先从这首词的历史背景来探求其创作原因。

图5 水力性能模拟与试验结果Fig.5 Simulation and experimental results of hydraulic performance
图6为上充泵大流量工况点的空化模拟与试验数据,NPSH为空化余量。由图6可见,NPSHR模拟值为6.12 m,试验值为6.35 m,两者均小于技术规范要求的7.8 m,其相对误差为3.6%。综合水力性能试验和空化试验数据可认为模拟结果是正确的。
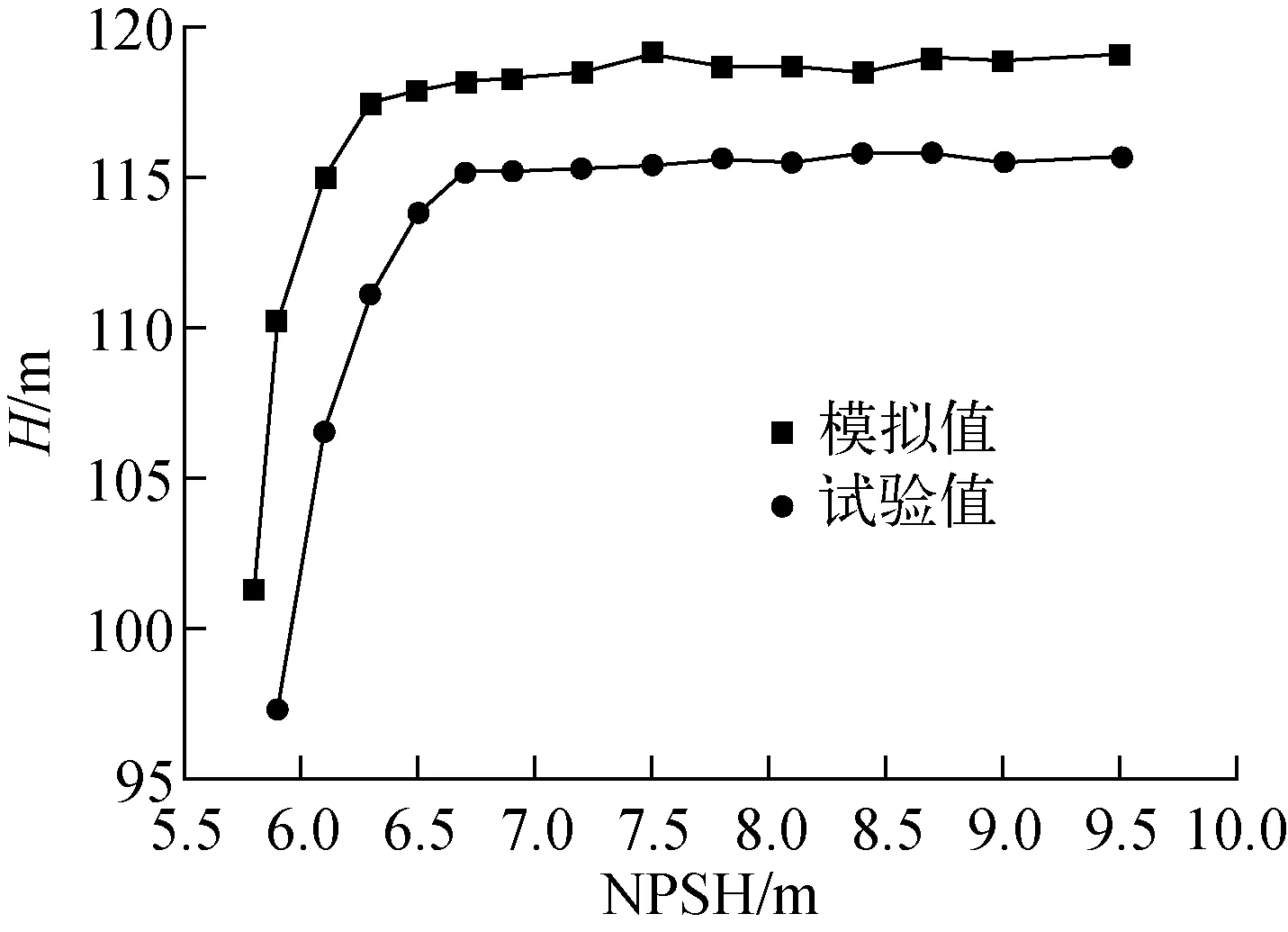
图6 空化模拟与试验结果Fig.6 Results of cavitation simulation and experiment
4 空化特性分析
4.1 监测点设置与空化状态分类
非定常计算中以定常计算的结果作为初始值。叶轮每转3°作为一个时间步长,时间步长为1.111×10-4s,叶轮旋转9个周期,总计算时间为0.12 s,经过3个周期后计算趋于稳定,选后6个周期进行分析。在叶轮流道中,从进口到出口均匀取Ⅰ、Ⅱ、Ⅲ监测点,所有监测点均取在中截面上,如图7所示。
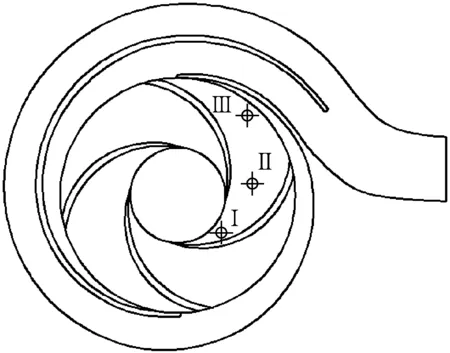
图7 监测点位置Fig.7 Position of monitoring point
静压值统一转化成无量纲的压力系数Cp,其定义为:
(1)
其中:u2为叶轮出口圆周速度;p为静压;ρ为密度。
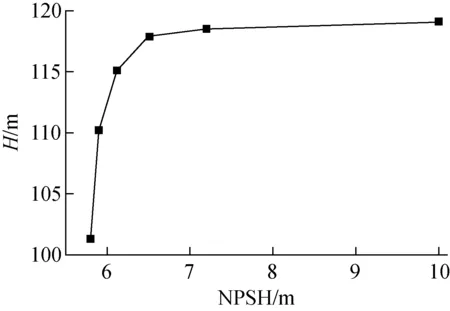
图8 5种空化状态Fig.8 Five kinds of cavitation states
文献[7-9]对空化状态的分类不同,学术界对空化状态的细分也无统一标准。在试验验证了数值计算可靠性的前提下,本文将叶轮空化分为5个阶段,分别是初生空化、发展空化、临界空化、严重空化和断裂空化,如图8所示。图8中,从右往左依次选取6个点进行分析:第1个点是正常工况,NPSH=10 m;第2个点是初生空化状态,NPSH=7.2 m;第3个点是发展空化状态,NPSH=6.5 m,此时泵扬程效率等没有发生明显变化;第4个点为临界空化状态,NPSH=6.12 m,对应泵扬程下降了3%;第5个点是严重空化状态,泵扬程下降了7.5%,NPSH=5.9 m;第6个点是断裂空化状态,扬程下降了15%,NPSH=5.8 m,此时进一步降低进口压力,扬程迅速陡降,空化试验很难再进行下去。
4.2 汽泡分布规律
为更好分析汽泡分布规律,给出汽泡沿叶轮径向位置的分布,如图10所示。图10中,R为径向半径,φ为汽泡体积分数。本文中叶轮轮毂直径为100 mm,外径为236 mm,因此径向半径为0.05~0.118 m。由图10可见:初生空化状态下,汽泡主要分布在叶轮进口侧0.05~0.057 m的位置,汽泡体积分数最大也仅为0.61;发展空化状态下,汽泡沿径向延伸到0.067 m的位置,最大汽泡体积分数也增加到0.74;临界空化状态下,汽泡主要分布在叶轮进口侧0.05~0.075 m的位置,汽泡数量大大增加,汽泡体积分数最大高达0.87;当达到严重空化状态时,汽泡沿径向延伸到0.087 m的位置,最大汽泡体积分数增加到0.92;断裂空化状态下,汽泡迅速蔓延到叶轮出口侧,靠近出口侧0.09~0.118 m位置的汽泡数量急剧增加,汽泡充斥整个叶轮流道内部。
4.3 压力脉动特性
不同空化状态下的叶轮内静压脉动如图11所示。图11中横坐标为步长,120步为1个周期,共720步。正常情况下,每个周期中叶轮内各监测点的压力脉动均很规律。叶轮进口处点Ⅰ的压力系数Cp在0.24~0.27范围内小幅度波动,点Ⅱ处Cp在0.37~0.45范围内小幅度波动,点Ⅲ处Cp明显大于点Ⅰ和点Ⅱ,在0.49~0.64范围内小幅度波动。越靠近叶轮出口处压力脉动幅值越大。初生空化状态下,叶轮内压力脉动仍较为规律,和图11a相比压力略有下降,脉动幅度略有上升。发展空化状态下,空化与叶轮蜗壳之间的动静干涉共同影响叶轮内的流场分布,使得叶轮内的压力脉动规律变得较为杂乱,大约需要2.5个周期,叶轮内的压力脉动才能完成1次完整的变化,且每次变化的脉动规律也有一定的差别。点Ⅰ处Cp最小值为0.1,最大值为0.27,差值为0.17;点Ⅱ处Cp最小值为0.25,最大值为0.44,差值为0.19;点Ⅲ处Cp最小值为0.34,最大值为0.64,差值为0.3。从叶轮进口到出口,点Ⅰ、Ⅱ和Ⅲ的瞬态压力逐渐增加,压力脉动幅度也越来越大。临界空化状态下,叶轮内各点的压力脉动更加紊乱,不同周期之间波动也无明显相似的规律。其中两个周期点Ⅰ的瞬态压力接近0,出现较大的波谷,而点Ⅱ、Ⅲ压力脉动尽管依然不规律,但未出现太大的突变。这是由于点Ⅰ处于叶轮进口处,此时汽泡和水流运动共同干扰点Ⅰ处的流场,使得点Ⅰ的压力脉动极为紊乱。严重空化状态下,点Ⅰ处Cp最小值为0.03,最大值为0.08,差值为0.05;点Ⅱ处Cp最小值为0.27,最大值为0.34,差值为0.07;点Ⅲ处Cp最小值为0.38,最大值为0.54,差值为0.16。点Ⅱ、Ⅲ处的压力脉动重新变得较为规律;点Ⅰ处压力脉动在后3个周期仍然比较杂乱,证明此时叶轮进口处大量的汽泡依旧无规则地干扰点Ⅰ的脉动规律。可见严重空化状态下,空化替代叶轮蜗壳动静干涉,逐渐成为控制叶轮流道内压力脉动规律的主要因素,各点的压力脉动慢慢变得较为稳定。断裂空化状态下,点Ⅰ、Ⅱ处的瞬态压力接近0,波动程度很小,对比图9e可知,此时叶轮进口和中部均存在大量汽泡密集区域,点Ⅰ、Ⅱ正好都处于汽泡密集区,液态水很少,导致点Ⅰ、Ⅱ处的瞬态压力极低。点Ⅲ处Cp在后3个周期稳定后的平均压力脉动幅值为0.15,脉动很有规律。此时汽泡延伸到叶轮出口,并在叶轮出口和蜗壳内的高压区域迅速溃灭,对叶片和泵体产生剧烈冲击,空化试验时会听到有规律的振动声,叶轮出口有较强烈且有规律的振动,导致点Ⅲ处存在比较规律且幅值较高的压力脉动。此时空化已完全成为控制叶轮流道内压力脉动规律的主要因素。

a——初生空化;b——发展空化;c——临界空化;d——严重空化;e——断裂空化

a——初生空化;b——发展空化;c——临界空化;d——严重空化;e——断裂空化
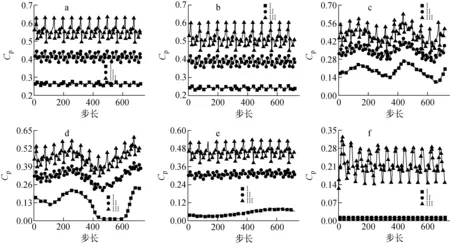
a——正常情况;b——初生空化;c——发展空化;d——临界空化;e——严重空化;f——断裂空化
最后1个周期不同空化状态下的叶轮内压力脉动频域如图12所示。图12中,f为频率。本文中叶轮转速为4 500 r/min,叶片数为4,因此转频为75 Hz[10-11]。结合图12a、b可看出,初生空化状态下,由于汽泡很少,对泵运行几乎无影响,因此图12a、b差别很小。从叶轮进口到出口,随着压力的升高,点Ⅰ、Ⅱ、Ⅲ的主频幅值逐渐增加,各点主频均为150 Hz,是转频的2倍。发展空化状态下,主频幅值翻倍增加,点Ⅰ、Ⅱ、Ⅲ的主频幅值分别为0.061、0.059、0.074,分别是初生空化时的6.4倍、2.8倍和1.6倍。此时各点主频均在转频75 Hz处,相差不大,中高频区压力脉动更为紊乱,衰减速度更快。临界空化状态下,点Ⅱ、Ⅲ的主频幅值很小,仅为0.034和0.032,点Ⅰ处的主频幅值远大于另外两个点,高达0.157,这与图11d中点Ⅰ的压力脉动极不规律,并出现较小的极值相对应。3个点主频全部在转频75 Hz处。严重空化状态下,主频幅值从叶轮进口到出口依次增加,点Ⅰ、Ⅱ、Ⅲ处的主频幅值分别为0.005、0.019和0.041。点Ⅰ的主频出现在转频75 Hz处,点Ⅱ、Ⅲ的主频出现在150 Hz处。断裂空化状态下,由于叶轮进口和中部位置存在大量汽泡,点Ⅰ、Ⅱ的瞬态压力值极低,对应的脉动幅值很小,点Ⅰ、Ⅱ的主频幅值几乎相等,均为0.006,出现在转频75 Hz处。点Ⅲ的主频幅值为0.076,出现在150 Hz处。这和图11e相对应,叶轮出口侧仍保持较规律的压力脉动和较高的主频幅值,且中高频部分的频率急剧衰减。综合图12可看出,叶轮内压力脉动主要产生在低频区,并呈现周期性降低的趋势,主频及次主频幅值均为转频的整数倍。
需要补充说明的是,上充泵为低比转速泵,而不同类型的泵在不同空化状态下的表现不一定相同,但可以本文叙述的方法为基础去研究其他类型泵的空化特点。
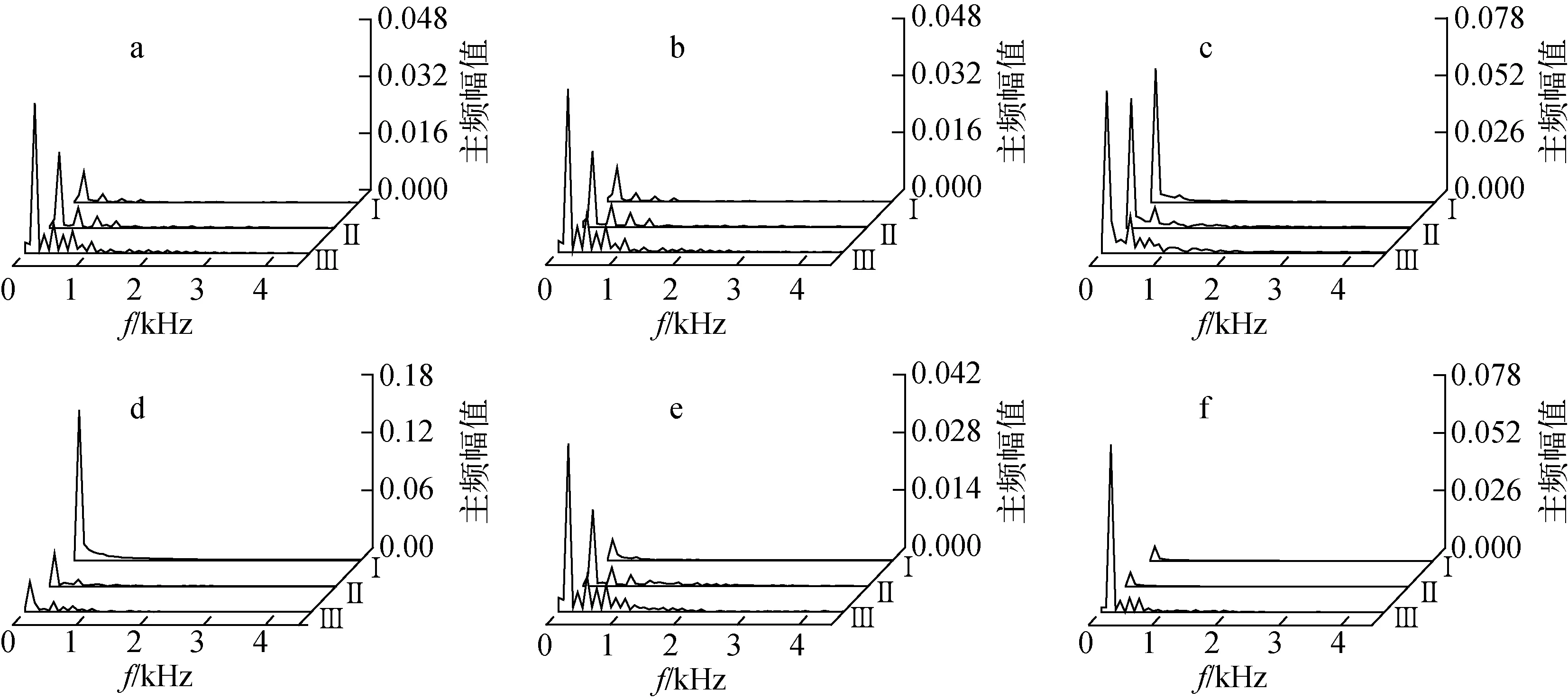
a——正常情况;b——初生空化;c——发展空化;d——临界空化;e——严重空化;f——断裂空化
5 结论
1) 增加叶片数会加剧进口排挤,但同时也会降低叶片工作面和背面的压差,前者会降低泵空化性能,后者会提高空化性能。通过计算选择了4叶片数方案,既保证了最佳空化性能,又有效提高了泵扬程和效率。
2) 最大流量工况点扬程模拟值与试验值的相对误差为2.9%,空化余量相对误差为3.6%,数值计算结果与试验结果的变化趋势相同,验证了数值模拟的可靠性。
3) 初生空化状态下汽泡主要分布在叶片进口背面处,随着空化程度的加深,叶轮流道内沿径向位置的汽泡数量迅速增加,临界空化状态下叶片背面也开始产生汽泡,断裂空化状态下汽泡充斥整个叶轮内部。
4) 从初生空化到断裂空化,叶轮流道内部压力脉动呈现比较规律→逐渐不规律→极不规律→逐渐规律→比较规律的变化过程。在发展空化到严重空化状态之间,由于空化和叶轮蜗壳动静干涉共同影响,叶轮内压力脉动较为杂乱,脉动幅值较大。当达到严重空化状态后,空化成为控制叶轮内压力脉动规律的主要因素,压力脉动变得相对稳定。断裂空化时叶轮进口和中部处的瞬态压力剧烈下降,脉动幅值很小,但出口处仍然保持幅值较高且比较规律的压力脉动。
[1] 许德忠,孔令杰,林冲. CPR 1 000 MW核电站上充泵介绍[J]. 水泵技术,2007(6):9-14.
XU Dezhong, KONG Lingjie, LIN Chong. Introduce of charging pump in CPR 1 000 MW nuclear power plants[J]. Pump Technology, 2007(6): 9-14(in Chinese).
[2] JNES. Break of charging pump main shaft: Ikata power station Unit-3[R]. Japan: Currentstatus of Nuclear Facilities in Japan, 2004.
[3] 王延合,于水. 300 MW核电站上充泵的设计[J]. 水泵技术,1999(2):6-9.
WANG Yanhe, YU Shui. The charging pump design in 300 MW nuclear power plants[J]. Pump Technology, 1999(2): 6-9(in Chinese).
[4] 付强,袁寿其,朱荣生,等. 1 000 MW级核电站离心式上充泵转子轴系的扭振特性[J]. 排灌机械工程学报,2013,31(5):394-400.
FU Qiang, YUAN Shouqi, ZHU Rongsheng, et al. Torsional vibration characteristics of rotor for centrifugal charging pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(5): 394-400(in Chinese).
[5] COUITER-DELGOSHA O, FORTES-PATELLA R,REBOUD J L. Experimental and numerical studies in a centrifugal pump with two-dimensional curved blades in cavitating condition[J]. Journal of Fluids Engineering, 2003, 125: 970-978.
[6] 王维军,王洋,刘瑞华,等. 离心泵空化流动数值计算[J]. 农业机械学报,2014,45(3):37-44.
WANG Weijun, WANG Yang, LIU Ruihua, et al. Numerical simulation of cavitation flow in a centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(3): 37-44(in Chinese).
[7] 张德胜,施卫东,郎涛,等. 特种涡轮驱动混流泵瞬态空化特性[J]. 华中科技大学学报:自然科学版,2014,42(2):40-45.
ZHANG Desheng, SHI Weidong, LANG Tao, et al. Transient cavitation characteristics of a special mixed-flow turbopump[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 2014, 42 (2): 40-45(in Chinese).
[8] 刘厚林,刘东喜,王勇,等. 三种空化模型在离心泵空化流计算中的应用评价[J]. 农业工程学报,2012,28(6):54-59.
LIU Houlin, LIU Dongxi, WANG Yong, et al. Applicative evaluation of three cavitating models on cavitating flow calculation in centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(6): 54-59(in Chinese).
[9] 王松林,谭磊,王玉川. 离心泵瞬态空化流动及压力脉动特性[J]. 振动与冲击,2013,32(22):168-172.
WANG Songlin, TAN Lei, WANG Yuchuan. Characteristics of transient cavitation flow and pressure fluctuation for a centrifugal pump[J]. Journal of Vibration and Shock, 2013, 32(22): 168-172(in Chinese).
[10]王秀礼,袁寿其,朱荣生,等. 基于CFD数值模拟的复合叶轮核主泵压力脉动特性研究[J]. 原子能科学技术,2014,48(1):99-105.
WANG Xiuli, YUAN Shouqi, ZHU Rongsheng, et al. Numerical simulation on pressure fluctuation of reactor coolant pump with complex impeller based on CFD technique[J]. Atomic Energy Science and Technology, 2014, 48(1): 99-105(in Chinese).
[11]张宁,杨敏官,李忠,等. 侧壁式压水室离心泵的压力脉动特性[J]. 机械工程学报,2012,48(14):164-168.
ZHANG Ning, YANG Minguan, LI Zhong, et al. Pressure pulsation of centrifugal pump with tilt volute[J]. Chinese Journal of Mechanical Engineering, 2012, 48(14): 164-168(in Chinese).
Cavitation Characteristics and Experimental Study on the First Stage Impeller of Centrifugal Charging Pump
ZHU Rong-sheng, JIANG Xu-song, FU Qiang, LONG Yun, WANG Xiu-li, XI Yi
(ResearchCenterofFluidMachineryEngineeringandTechnology,JiangsuUniversity,Zhenjiang212013,China)
In order to study and improve cavitation performance of the first stage impeller of centrifugal charging pump in nuclear power plant, the numerical simulation was used for optimization and analysis. The number of the blades was changed to 4, and the best cavitation performance, the head and efficiency of pump were studied. The results show that in the maximum flow rate condition, the relative error of head between simulation and experimental results is 2.9% and the relative error of net positive suction head is 3.6%. The numerical results and experiment results are consistent. The cavitation is divided into 5 stages: incipient cavitation, developing cavitation, critical cavitation, severe cavitation and fracture cavitation. The analysis results indicate that the bubbles appear firstly in the inlet of the blade suction surface in incipient cavitation and they appear in the blade pressure surface after critical cavitation. The cavitation and dynamic and static interference in the pump body affect pressure fluctuation in the impeller between developing cavitation and severe cavitation. The cavitation plays a main role after severe cavitation, then pressure fluctuation becomes relatively stable and amplitudes of pressure fluctuation significantly reduce in the inlet and central part of the impeller, but pressure pulsation with relatively high amplitude and regularity still remains in the impeller outlet.
charging pump; the first stage impeller; cavitation; pressure pulsation; numerical simulation
2014-06-08;
2014-11-25
国家自然科学基金资助项目(51379091);国家科技支撑计划资助项目(2011BAF14B04);江苏省自然科学基金科技项目资助(BK20130516);江苏高校优势学科建设工程资助项目(PDPA)
朱荣生(1964—),男,湖南永州人,研究员,博士,从事流体机械水力设计及内部流动研究
TH212;TH213.3
A
1000-6931(2015)10-1778-08
10.7538/yzk.2015.49.10.1778

