升潜条件下矩形窄缝通道绝热层流流动解析解

周 磊，葛 超，昝元锋，闫 晓，陈炳德

(1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室，四川 成都 610041；2.中核核电运行管理有限公司，浙江 嘉兴 314300)



升潜条件下矩形窄缝通道绝热层流流动解析解

周 磊1，葛 超2，昝元锋1，闫 晓1，陈炳德1

(1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室，四川 成都 610041；2.中核核电运行管理有限公司，浙江 嘉兴 314300)

本文采用数学分析方法对矩形窄缝通道内绝热层流流动进行了研究。通过合理简化得到了分析对象的控制方程，基于固定流量和固定通道压降两种不同的边界条件，求解得出方程的解析解，从而可定量分析升潜条件对速度分布、压降、摩阻系数等的影响规律。

升潜条件；矩形窄缝；绝热层流；解析解

和陆基反应堆不同，由于自身机动和风、浪、涌的影响，船用反应堆处于瞬变的时空场，受到运动附加力的影响。升潜作为一种典型的海洋条件，对热工水力特性的影响是一值得学术界和工程界关注的问题。国外的一些先进反应堆采用了板型燃料元件以便减小装置体积、提高堆芯功率密度，其冷却剂流道为矩形窄缝。绝热层流流动物理过程较简单，从而有望获得解析解来作为实验对比和程序验证的基准，也可为其他复杂热工问题提供定性参考。

文献[1]对竖直和水平放置、摇摆运动条件下的圆管单相水摩擦阻力特性进行了实验研究，结果发现在摇摆条件下竖直管内单相摩擦阻力系数不仅是雷诺数的函数，而且还受管径、摇摆周期以及摇摆角度的影响。文献[2]针对科氏加速度对阻力特性的影响进行了研究，研究结果表明垂直于流动方向的附加科氏惯性力对流动阻力的影响可以忽略。文献[3]通过实验的方法研究了升潜和摇摆条件下矩形窄缝通道的绝热单相流动阻力特性，并采用CFX对实验结果进行了模拟。文献[4]采用实验、理论和大涡模拟等手段对典型海洋条件下加热矩形窄缝通道的单相流动阻力特性进行了研究，其中在理论研究方面，基于轴向一维流体动力学主导机制，分别在层流和湍流流态下，通过解析方法和零方程模型结合壁面函数方法求解海洋条件下矩形窄缝通道内层流和湍流速度及温度分布，初步建立海洋条件下矩形窄缝通道内单相流动及传热理论模型。文献[5]对于固定流量的矩形窄缝通道，分别求得了绝热和加热条件下单相层流流动的理论解和阻力系数。

以上研究主要是实验研究和数值模拟，理论求解相对较少，且研究仅针对固定流量这一种边界条件，使得研究结论局限较大。本文在已有研究的基础上，基于固定流量和固定压差两种边界条件，研究升潜条件下矩形窄缝通道绝热层流流动的解析解，为相关的实验分析和程序开发提供参考。

1 基本假设和方程简化

为获得有意义的解析解，作出以下假设。

1) 流体不可压缩

绝热条件下流体为等温流动，密度不发生改变；层流流速远低于声速，此时液体的压缩性可完全忽略。

2) 流动简化为二维流动，即不考虑在宽边方向上的变化

矩形窄缝通道及其坐标系的设置如图1所示。矩形窄缝通道的间隙一般不大于3 mm，而通道宽边尺寸远大于窄边，因而作出以上假设是合理的，并能使问题得到简化。

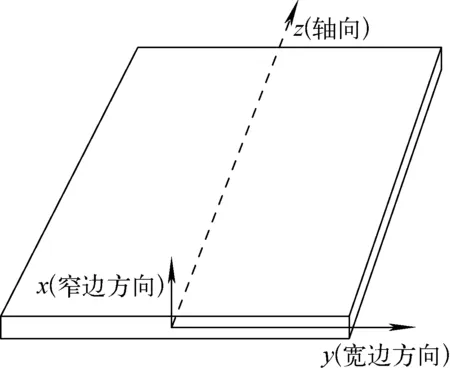
图1 矩形窄缝通道示意图Fig.1 Schematic graph for narrow rectangular gap

3) 平行流动，无二次横流

本文分析的对象是窄间隙通道内的绝热流动，升潜条件只改变竖直方向体积力的大小，在横向上既无体积力分量，也无流体密度梯度，因此不存在横向流动。

二维不可压缩流动的控制方程[6]为：

(1)

(2)

(3)

其中：v为流体速度，m/s；t为时间，s；p为压力，Pa；ρ为流体密度，kg/m3；ν为运动黏度，L2/s；f为单位质量流体受到的外力，m/s2。升潜条件下流体只受到竖直方向的外力，因此：

(4)

其中：g为重力加速度；a(t)为升潜加速度。

根据假设3有：

(5)

由此质量守恒方程变为：

(6)

而x方向(横向)的动量方程可简化为：

(7)

即压力与x无关，仅与z有关。在z方向(流向)动量方程可简化为：

(8)

下文中，以符号u代替vz以便书写更简洁。因式(6)指出速度与z无关，可知u=u(x,t)。

2 竖直静止条件的基准解

静止条件下的解可作为比较的基准，同时也可作为瞬态求解的初始条件，因此求解是必要的。另外，静止条件下定流量或定压差边界条件是不独立的，求解一种即可。

壁面无滑移条件为：

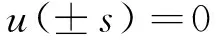
(9)

其中，s为窄缝宽度的一半。

(10)

根据z方向动量方程(式(8))可得到：

(11)

式(11)左边是z的函数，右边是x的函数，因此两边都只能是常数c，即：

(12)

积分之，流速为二次多项式：

(13)

根据平均流速的定义：

(14)

得到常数c为：

(15)

从而速度的解为：

(16)

式(16)为抛物型的速度分布。通过式(12)积分还可得出压力：

(17)

通道的总压降为：

(18)

其中：pi、po分别为通道进、出口压力，Pa；μ为动力黏度，Pa·s；L为通道长度，m。

式(18)第1项为摩擦压降，第2项为重力压降。式(18)表明对于特定的通道，压降与流量或平均流速存在唯一对应关系。根据摩阻系数的定义：

(19)

其中：Δpf为摩擦压降，Pa；λ为摩阻系数；De为通道水力直径，m，其定义为：

De=4a/ξ≈4s

(20)

其中：a为通道截面积，m2；ξ为通道湿周，m。

由式(18)可得出：

(21)

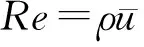
(22)

根据壁面摩擦应力也可计算摩阻系数：

(23)

3 升潜条件方程求解

和静态条件不同，升潜条件引入了时变性的附加力。因此根据给定的边界条件的不同，解将可能存在明显的不同。

3.1 定流量或平均流速

在强迫循环条件下，流量受到泵等动力源的驱动，由于液体的压缩性很小，所以通过测量段的流量或平均流速是固定的。这就是定流量或平均流速的情况。此时因流速与时间无关，控制方程变为：

(24)

(25)

对压力作如下变换：

(26)

则可发现关于流速u和变量pE的方程在形式上和静态条件完全相同，从而可解出：

(27)

(28)

(29)

其中，a(t)=amsinωt，am和ω分别为最大升潜加速度和角频率。

可见在固定流量条件下，升潜运动仅改变了通道的压降，使其和升潜运动呈同周期变化。这是由于合成重力发生改变使得提升压降发生变化的缘故。升潜运动不改变速度分布形状和摩阻系数。

3.2 给定压差

对一些由海水冷却的开式回路，或测量段入口有一理想的稳压器稳定压力、出口直接和大气空间相连，均可看作等压差边界。因升潜运动使得重力压降随时间作周期性改变，而通道压降保持不变，因此流速必然是瞬态变化，是与时间有关的变量。

此时轴向动量方程转化为：

(30)

由于方程和定解条件均是线性的，因此若u1和u2分别满足下述方程，那么它们的和必然满足式(30)[7]：

(31)

(32)

对于式(31)，形式上和竖直静止条件下的方程完全相同，因此其定解为：

(33)

可将式(33)作为初始条件。

对于式(32)，可采用分离变量法，令u2=Υ(f(x)eiωt)(其中，Υ表示取复数的实部，f(x)为空间坐标的函数)，将其代入式(32)可得：

(34)

其中，f″为f(x)的二阶导数。

式(34)是一个二阶非齐次线性常微分方程，它的解是特解加上齐次方程的通解构成。该方程的特解为：

(35)

根据常微分方程理论，齐次方程的通解[7]为：

(36)

其中，k1、k2分别为待定系数。

根据无滑移边界条件可解出：

(37)

故式(30)的复数解为：

(38)

利用公式：

sinh(a+ib)=sinha·cosb+isinb·cosha

(39)

cosh(a+ib)=cosha·cosb+isinb·sinha

(40)

可得到流速为：

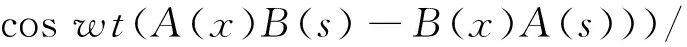
(41)

其中：

(42)

(43)

再利用初始条件得到：

(44)

最终得到速度为：

(45)

可以验证，它确实满足边界条件和初始条件。根据解的唯一性，证实它就是方程的解。式(45)第1项是重力作用下的泊肃叶流动，它只能提供等压降。第2项是附加力引起的波动速度，产生波动性的压降，且波动幅度和横向坐标x有关。

在壁面上(x=s)对上式求导数可得到剪切应力，进而求得摩阻系数为：

(46)

式(46)中，雷诺数是按照时间平均的流速定义的。定义升潜加速度数Nhea和无量纲窄缝宽度数Ngeo如下：

(47)

(48)

它们分别表征升潜运动附加力和惯性力的相对大小以及黏性作用的横向衰减效应。则升潜条件下摩阻系数可表示为：

(49)

由式(49)可见摩阻系数也是波动的，它的波动中心就是静态条件下的摩阻系数，而波动幅度与升潜加速度数及通道间隙有关。

综上，在固定通道压降的情况下，速度分布和摩阻系数均发生改变，从而摩擦压降和重力压降均波动变化，但总压降保持不变。

4 结论

本文对升潜条件下矩形窄缝通道内绝热层流流动进行了理论研究，主要结论如下。

1) 根据矩形窄缝通道和绝热流动的特征，可将流动过程简化为二维不可压缩平行流动。

2) 求得了静态条件下的理论解，速度分布是抛物型分布曲线，结果和已有研究相符。

3) 求得了升潜条件下两种不同边界条件的理论解。当给定通道平均流速时，升潜条件不改变速度分布形状和摩阻系数，只引起通道内重力压降和总压降的周期性变化；当固定通道的压差时，周期性变化的运动附加力将引起流量的波动，从而使得摩阻系数也发生周期性的变化，这一点在工程应用中尤其应引起注意。

[1] 曹夏昕，阎昌琪，孙立成，等. 摇摆状态下竖直管内单相水阻力特性实验研究[J]. 核动力工程，2007，28(3)：51-55.

CAO Xiaxin, YAN Changqi, SUN Licheng, et al. Pressure drop characteristic of single-phase flow in vertical rolling pipes[J]. Nuclear Power Engineering, 2007, 28(3): 51-55(in Chinese).

[2] 杜思佳. 海洋条件对单相强迫循环流动影响的理论研究[D]. 北京：清华大学工程物理系，2011.

[3] 刘晓钟. 加速度对矩形通道单相流动特性影响研究[D]. 成都：中国核动力研究设计院，2011.

[4] 马建. 运动条件下窄缝矩形通道内单相强迫流动及传热研究[D]. 重庆：重庆大学动力工程及工程热物理系，2012.

[5] 鄢炳火，匡波. 外力场作用下单相流体动力学特性模型研究[R]. 成都：中国核动力研究设计院，2013.

[6] 张鸣远，景思睿，李国君. 高等工程流体力学[M]. 西安：西安交通大学出版社，2006.

[7] 梁昆淼. 数学物理方法[M]. 北京：高等教育出版社，1995.

Analytical Solution of Adiabatic Laminar Flow in Narrow Rectangular Gap under Heaving Condition

ZHOU Lei1, GE Chao2, ZAN Yuan-feng1, YAN Xiao1, CHEN Bing-de1

(1.CNNCKeyLaboratoryonNuclearReactorThermal-hydraulicsTechnology,NuclearPowerInstituteofChina,Chengdu610041,China;2.NuclearPowerOperationandManagementCo.,Ltd.,Jiaxing314300,China)

Adiabatic laminar flow in narrow rectangular gap under heaving condition was analytically studied in this paper. First of all, reasonable assumptions were made and the governing equations of flow were hence simplified. Then analytical solutions were derived based on fixed inlet flow rate and fixed pressure drop boundary conditions. Thus the influences of heaving condition on velocity profile, pressure drop and frictional coefficient can be studied quantitatively.

heaving condition; narrow rectangular gap; adiabatic laminar flow; analytical solution

2014-03-21;

2014-11-11

周 磊(1984—)，男，四川南充人，副研究员，博士，核能科学与工程专业

TL333

A

1000-6931(2015)07-1215-05

10.7538/yzk.2015.49.07.1215