例说积分在经济学中的应用
罗 琼
(江西财经职业学院,江西九江 332000)
例说积分在经济学中的应用
罗 琼
(江西财经职业学院,江西九江 332000)
随着经济的快速发展以及计算机技术和数学软件的不断开发,数学知识和数学分析方法在现代经济建设中的作用愈发突出。积分特别是定积分作为一种量化分析工具在经济学中应用十分广泛,可以求经济总量及其平均值或变动值、求解最大最小值、算资本现值和资本存量、计算消费者剩余和生产者剩余等等。
积分;经济学;资本现值;消费者剩余;生产者剩余
在如今的知识经济时代,计算机技术和数学软件不断被开发出来,数学知识的应用已经深入到社会的各个领域。高等数学中的积分作为一种量化分析的工具在经济学中的应用就十分广泛,涉及内容很多,如求经济总量及其平均值或变动值、求解经济函数最大或最小值、算资本现值和资本存量、计算消费者剩余和生产者剩余等等。以下分别举例说明。
1 求经济总量及其平均值或变动值
变化率(即边际)和弹性是经济分析中常用的概念。已知某一经济量(如需求、成本、收入或利润)的变化率(即边际)或弹性函数,则可以用不定积分或一个变上限的定积分来求出原经济总量及其平均值,如果要求它在某个范围内的改变量,就直接用定积分解决。
例1 设某产品的边际成本函数C'(q)=60-2q(万元/年),固定成本C(0)=100(万元),求总成本函数和平均成本函数。
解1 总成本函数C(q)是边际成本函数的原函数,因此
C(q)=∫C'(q)dq=∫(60-2q)dq=60q-q2+c,又C(0)=100,得c=100,所以,
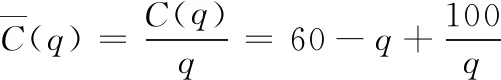
例2 某汽车的需求价格弹性为-2,其售价为10万元/辆时,需求量为 2万辆,求此汽车的需求函数。
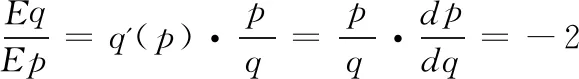
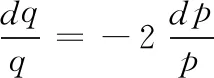

例3 设某产品总收益的变化率R'(q)=50-q(元/件),求从10件增加到20件时,总收益及平均收益的变化量。

即从10件增加到20件时,总收益增加350元,平均收益增加35元/件。
2 求解经济函数最大最小值
众所周知,企业经营永远力求在现有条件下成本最低或利润最大。所以,经济分析中常遇决策优化问题。若已知某经济量的边际,可用积分求出原经济函数,再利用极值原理求其最值。
例4 某产品产量为x台时,边际成本为MC=2x-10。若固定成本100万元,售价50万元/台,假定产销平衡,求最小平均成本和最大利润。

由L'(x)=40-2x=0,得唯一驻点x=20,且L"(20)=-2<0,所以,当产量为20台时利润最大,最大利润为L(20)=300万元。
3 算资本现值和投资
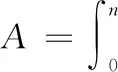
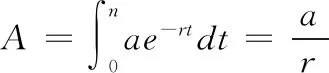
例5 某电器行推出一项分期付款的助销活动:某型号空调一次性付款要6999元,分期付款,则每月付850元,10个月付清。若现金的月利率为3%,试问哪种付款方式合算?
例6 某投资项目投资成本1万元,每年均匀收入2000元,投资年利率5%,且连续计息。试求:1)该投资的回收期;2)该投资为无限期时的纯收入贴现值。
解 1)投资回收期n就是当总收入的现值等于投资时的时间, 投资成本C= 1万元,

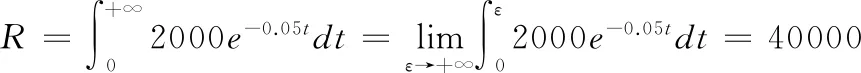
4 计算资本存量


5 计算消费者剩余和生产者剩余
消费者剩余CS和生产者剩余PS是经济福利分析的两个重要工具。消费者剩余是指消费者在购买一定数量的商品时愿意支付的总价格和实际支付的总价格之间的差额;生产者剩余是指生产者销售某种商品所得到的款额与其生产成本之间的差额。假设商品的需求函数和供给函数分别为P=D(q)和P=S(q),市场价格为p0时,购买量为q0(即均衡价格和均衡产量),则得如下消费者剩余和生产者剩余的计算公式:

例8 已知某蔬菜市场的需求函数为P=10-q,供给函数为P=7+0.5q,求消费者剩余与生产者剩余。
解:先求出市场均衡价格p0和均衡产量q0:由10-q=7+0.5q得p0=8,q0=2。
结 语
当然,积分在经济学中的应用还有很多,例如,通过积分量化分析期值和现值来进行固定资产投资与融资租赁的决择[2];已知服务行业服务概率的频率函数,求某个时间段内的服务概率[3];公司根据销售额的变化率,利用定积分计算盈利来决定广告策略问题等等,在此就不一一例说。随着经济、计算机技术等的不断发展,积分的应用会更加广泛,数学与经济管理的关系也将越发密切。
[1]蔡 琼,岳素青.定积分在经济管理中的应用[J].哈尔滨职业技术学院学报,2010,(3):116-117.
[2]龚友运.积分学在经济分析中的应用浅析[J].佳木斯教育学院学报,2011,(3):121-122.
[3]卢达平.《微积分》在经济管理中的应用[J].龙岩学院学报,2006,(6):109-111.
[4]仉志余.大学数学应用教程[M].北京:北京大学出版社,2005.160-164.
[5]赵树媛.经济应用数学基础(一)微积分(三版)[M].北京:中国人民大学出版社,2012.253-254.
[6]高鸿业.西方经济学[M].北京:中国人民大学出版社,2007.
Examples for the Application of Integration in Economics
LUO Qiong
(Jiangxi Vocational College of Finance and Economics, Jiujiang, Jiangxi, 332000)
With the rapid development of the economics and the constant exploitation of the computer technology and mathematical software, mathematical knowledge and its analytical methods are playing more and more important roles in the current economic construction. The application of integration, especially the definite integration in economics as a tool of quantitative analysis is very broad, which can be used to calculate economic aggregate and average or variation, maximum and minimum, present capital value and capital stock, consumer surplus and producer surplus or so on.
integration; economics; present capital value; consumer surplus; producer surplus
2015-04-09
罗 琼(1967-),女,湖南江华人,江西财经职业学院副教授。研究方向:数学及应用数学。
O172
A
1008-8156(2015)02-0070-03
修回日期:2015-05-12

