关于一类双曲线系的2个结论
●唐昊天 (复旦大学附属中学 上海 200433)
关于一类双曲线系的2个结论
●唐昊天 (复旦大学附属中学 上海 200433)
双曲线的弦长和双曲线系问题在平面解析几何中非常多见.笔者发现对于一类由平移变换形成的双曲线系存在一个有趣的弦长问题,下面向读者展示这个有关双曲线系和弦长的性质.

图1
图1中,该种平移变换的几何意义是使得双曲线中心O先沿着坐标轴方向平移到点P(0,t),然后点P再在根轴上运动.
性质1 平行或重合于平移双曲线系根轴的直线截平移双曲线系中所有双曲线所得弦长相等.
先考虑当t=0时情形.
将直线方程和平移双曲线系方程联立,得
b2(x-m)2-a2(kx+n-km)2=a2b2,
展开得
(b2-a2k2)x2+(-2a2kn-2b2m+2a2k2m)x+
(b2m2-a2n2-a2k2m2+2a2kmn-a2b2)=0,
从而
Δ=(-2a2kn-2b2m+2a2k2m)2-4(b2-a2k2)·
(b2m2-a2n2-a2k2m2+2a2kmn-a2b2)=4(a2b4-a4b2k2-a2b2n2),
因此直线截每一条双曲线所得的弦长(有弦长时)为
式中a,b,k,n取定时弦长为定值,故当t=0时结论成立.

性质2 截平移双曲线系中所有双曲线所得弦长相等的直线一定平行于平移双曲线系根轴.
证明 反证法.
先考虑当t=0时情形.
将直线方程和平移系方程联立,得
b2(x-m)2-a2(k′x+n-km)2=a2b2,
展开得
(b2-a2k′2)x2+(-2a2k′n-2b2m+2a2kk′m)x+
(b2m2-a2n2-a2k2m2+2a2kmn-a2b2)=0,
从而
Δ=(-2a2k′n-2b2m+2a2kk′m)2-4(b2-a2k′2)·
(b2m2-a2n2-a2k2m2+2a2kmn-a2b2)=4[a2b2n2+a2b4-a4b2k′2+2a2b2mn(k′-k)+a2b2m2(k′-k)2],

对于当t≠0时的情况,仿照性质1的证明作相同坐标变换可得弦长仍然是关于m的多项式,不可能是定值.
由反证法,命题“截平移双曲线系中所有双曲线所得弦长相等的直线一定平行于平移双曲线系根轴”得证.
下面的例题可以由上述性质解决:

解 双曲线方程可化为
设满足要求的直线方程为y=kx+n,由性质知k=2显然成立.代入性质1,可得
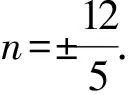

通过以上性质,笔者证明了这样一个有关双曲线系的有趣的“弦长为定值”结论.实际上这个问题在圆、椭圆等曲线系中也存在类似的结论,有兴趣的读者可以自行探究.

