关于不定方程x2-6y2=1与y2-Dz2=4的公解

杜先存，李玉龙

(红河学院 教师教育学院，云南 蒙自 661199)



关于不定方程x2-6y2=1与y2-Dz2=4的公解

杜先存，李玉龙

(红河学院 教师教育学院，云南 蒙自 661199)

利用递归序列、Pell方程的解的性质、Maple小程序等,证明了D=2n(n∈Z+)时，不定方程x2-6y2=1与y2-Dz2=4:(i)n=1时,有整数解(x,y,z)=(±485,±198,±140),(±5,±2,0)； (ii)n=3时,有整数解(x,y,z)=(±485,±198,±70),(±5,±2,0)； (iii)n=5时,有整数解(x,y,z)=(±485,±198,±35),(±5,±2,0)；(iv)n≠1,3,5时，只有平凡解(x,y,z)=(±5,±2,0).

Pell方程；递归序列；基本解；整数解；公解；奇素数

近年来，不定方程x2-D1y2=k与y2-Dz2=m的求解问题一直受到人们的关注.k=1,m=4时，已有如下一些结果：

(i)D1=2,D为奇数时，曹珍富[1]、曾登高[2]等就D最多为4个不同奇素数乘积的情况做过一些研究；

(ii)D1=2,D为偶数时，胡永忠、韩清[3]、管训贵[4]等对D的不同情况做过一些研究；

(iii)D1=6,D为奇素数时，苏小燕[5]已经解决；D至多含3个不同的奇素数时，冉银霞、冉延平[6]已经解决；

但笔者通过计算发现D=2n(n≥1,n∈N)时，方程x2-6y2=1 与y2-Dz2=4除了正整数解(x,y,z)=(485,198,35)外还有其他正整数解，文[9]解数不全是因为作者由“y2-22k-1z2=4”得到“z为奇数”(见文[9]第10页倒数第8行)，事实上，z为偶数也成立，所以作者少了z为偶数的两组解.论文利用与文[9]不同的初等方法得出了D=2n(n∈Z+)时方程x2-6y2=1 与y2-Dz2=4的全部正整数解.

1 引 理

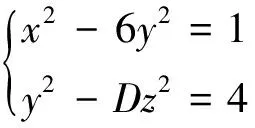
引理2[10]设D=2p,p是一个奇素数，则方程x4-Dy2=1(D>0且不是平方数)除了D=6,x=7,y=20外，无其他正整数解．

引理3 设Pell方程x2-6y2=1的全部整数解为(xn,yn),n∈Z,则对任意n∈Z,xn满足：xn为平方数当且仅当n=0或n=2.

证明 设(x1,y1)为Pell方程x2-6y2=1的基本解，则有(x1,y1)=(5,2).设(xn,yn),n∈Z+是Pell方程x2-6y2=1的正整数解，若xn=a2,代入原方程得a4-6y2=1.由引理2知，a4-6y2=1仅有正整数解(a,y)=(7,20),此时xn=49,从而n=2.又(1,0)是a4-6y2=1的平凡解，此时xn=1,从而n=0.所以n=0或n=2.反之，显然.

2 主要结论

定理 若D=2n(n∈Z+),则不定方程

(1)

的整数解的情况如下：

(i)n=1,有非平凡解(x,y,z)=(±485,±198,±140)和平凡解(x,y,z)=(±5,±2,0)；

(ii)n=3,有非平凡解(x,y,z)=(±485,±198,±70)和平凡解(x,y,z)=(±5,±2,0)；

(iii)n=5,有非平凡解(x,y,z)=(±485,±198,±35)和平凡解(x,y,z)=(±5,±2,0)；

(iv)n≠1,3,5,只有平凡解(x,y,z)=(±5,±2,0).

3 定理的证明

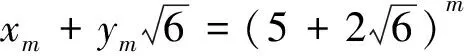
由文[8]知以下各式成立：

(I)y2m=2xmym；

(II)y2m-4=ym-1ym+1；

(III)xm≡1(mod2),y2m+1≡2(mod4)；

(IV) gcd(xm,ym)=gcd(xm,xm+1)=gcd(x2m+2,y2m+1)= gcd(x2m,y2m+1)=1；

(V) gcd(ym,ym+1)=2,gcd(x2m+1,y2m)=gcd(x2m+1,y2m+2)=5.

(2)

情形1m为偶数，则令m=2k,k∈Z,此时(2)成为

(3)

由(III)的y2m+1≡2(mod4)知，y2k-1≡y2k+1≡2(mod4),则有2‖y2k-1,2‖y2k+1,故(3)右边2的次数为2次，而(3)左边2的次数为2l-1次,矛盾，故此时(3)无整数解，则(1)无整数解.

情形2m为奇数，则令m=2k-1,k∈Z,此时(3)成为

(4)

由(I)得，(4)成为

(5)

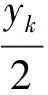
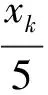
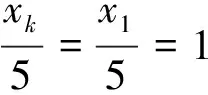
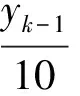
k=1时，(5)为22l-1z2=4x0y0x1y1=0,则z=0,故此时(1)只有平凡解(x,y,z)=(±5,±2,0).

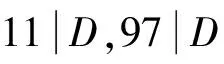
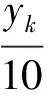
k=0时，(5)为22l-1z2=4x-1y-1x0y0=0,则z=0,故此时(1)只有平凡解(x,y,z)=(±5,±2,0).

k=2时，(5)为22l-1z2=4x1y1x2y2=4×5×2×49×20=25×52×72,则有z=±140,D=2或z=±70,D=23或z=±35,D=25.故n=1时,(1)有非平凡解(x,y,z)=(±485,±198,±140);n=3时,(1)有非平凡解(x,y,z)=(±485,±198,±70);n=5时,(1)有非平凡解(x,y,z)=(±485,±198,±35).

[1] 曹珍富. 关于Pell方程x2-2y2=1与y2-Dz2=4的公解[J].科学通报，1986,31(6)：476.

[2] 曾登高. 也说Pell方程x2-2y2=1与y2-Dz2=4的公解[J].数学的实践与认识，1995(1)：81-84.

[3] 胡永忠，韩清. 也谈不定方程组x2-2y2=1与y2-Dz2=4[J]. 华中师范大学学报：自然科学版：2002,36(1)：17-19.

[4] 管训贵.关于Pell方程x2-2y2=1与y2-Dz2=4的公解[J].华中师范大学学报：自然科学版：2012,46(3)：267-269,278.

[5] 苏小燕. 关于Pell方程x2-6y2=1与y2-Dz2=4的公解[J].漳州师范学院学报：自然科学版，2000,13(3)：35-38.

[6] 冉银霞，冉延平. 不定方程组x2-6y2=1,y2-Dz2=4[J].延安大学学报：自然科学版，2008，27(4)：19-21.

[7] 贺腊荣，张淑静，袁进. 关于不定方程组x2-6y2=1,y2-Dz2=4[J].云南民族大学学报：自然科学版，2012,21(1)：57-58.

[8] 杜先存，管训贵，杨慧章．关于不定方程组x2-6y2=1与y2-Dz2=4的公解[J]．华中师范大学学报：自然科学版,2014，48(3)：310-313.

[9] 王冠闽，李炳荣. 关于Pell方程x2-6y2=1与y2-Dz2=4的公解[J].漳州师范学院学报：自然科学版，2002,15(4)：9-14.

[10] 曹珍富.丢番图方程引论[M].哈尔滨：哈尔滨工业大学出版社，1989：262，273.

(责任编辑 朱夜明)

On the system of Diophantine equationsx2-6y2=1 andy2-Dz2=4

DU Xian-cun ， LI Yu-long

(College of Teacher Education, Honghe University , Mengzi 661199, China)

By using recursive sequence ,some properties of the solutions to Pell equation and Maple formality, the following conclusions were proved：IfD=2n(n∈Z+),then(i)thesystemofDiophantineequationsx2-6y2=1andy2-Dz2=4hasintegersolutions(x,y,z)=(±485,±198,±140),(±5,±2,0)wheren=1; (ii)thesystemofDiophantineequationsx2-6y2=1andy2-Dz2=4hasintegersolutions(x,y,z)=(±5,±2,0),(±485,±198,±70)wheren=3; (iii)thesystemofDiophantineequationsx2-6y2=1andy2-Dz2=4hasintegersolutions(x,y,z)=(±5,±2,0),(±485,±198,±35)wheren=5;(iv)thesystemofDiophantineequationsx2-6y2=1andy2-Dz2=4hasonlytrivialsolution(x,y,z)=(±5,±2,0)wheren≠1,3,5.

Pell equation; recursive sequence; fundamental solution; integer solution; common solution; odd prime

10.3969/j.issn.1000-2162.2015.06.004

2014-09-15

国家自然科学基金资助项目(11071194)；云南省教育厅科研基金资助项目(2014Y462)； 喀什师范学院校级课题基金资助项目((14)2513);红河学院校级课题基金资助项目(XJ15Y22)

杜先存(1981-)，女，云南凤庆人，红河学院副教授.

O

A

1000-2162(2015)06-0019-04